
网址:http://www.1010jiajiao.com/paper/timu/5154726.html[举报]
22.(本小题满分14分)
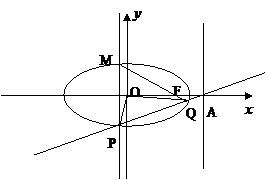 椭圆的中心是原点O,它的短轴长为
椭圆的中心是原点O,它的短轴长为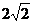 ,相应于焦点F(c,0)(
,相应于焦点F(c,0)(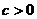 )的准线
)的准线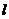 与
与 轴相交于点A,|OF|=2|FA|,过点A的直线与椭圆相交于P、Q两点。
轴相交于点A,|OF|=2|FA|,过点A的直线与椭圆相交于P、Q两点。
(1)求椭圆的方程及离心率;
(2)若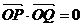 ,求直线PQ的方程;
,求直线PQ的方程;
(3)设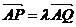 (
(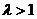 ),过点P且平行于准线
),过点P且平行于准线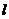 的直线与椭圆相交于另一点M,证明
的直线与椭圆相交于另一点M,证明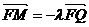 。
。
江苏省姜堰高级中学2007届第十次综合考试数学试卷答案07。03。18
一、选择题
CDBBA BBCCA
二、填空题
11.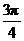 12.2 13.
12.2 13.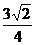 14.
14.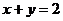 或
或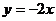
15. 16.②④⑤
16.②④⑤
三、解答题
17.解:(I)∵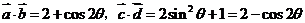 (2分)
(2分)
∴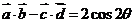 ,
(4分)
,
(4分)
∵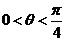 ,∴
,∴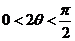
∴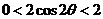 ,∴
,∴ 。 (6分)
。 (6分)
(II)∵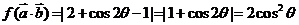 ,
,
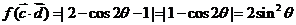 , (8分)
, (8分)
∴ ,
(10分)
,
(10分)
∵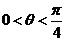 ,∴
,∴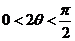 ,∴
,∴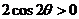 ,
,
∴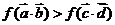 。 (12分)
。 (12分)
18.解:(Ⅰ) 直线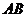 方程为
方程为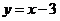 ,设点
,设点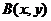 ,
(2分)
,
(2分)
由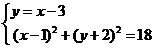 (4分)
(4分)
及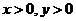 ,得
,得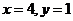 ,
,
∴点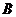 的坐标为
的坐标为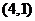 (6分)
(6分)
(Ⅱ)由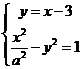 得
得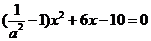 ,
(9分)
,
(9分)
设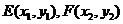 ,则
,则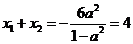 ,得
,得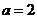 , (12分)
, (12分)
此时,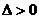 ,∴
,∴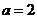 。
(14分)
。
(14分)
(注:缺少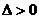 扣1分,
扣1分,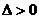 这个不等式可解可不解。)
这个不等式可解可不解。)
19.证明:(Ⅰ)证明 因为底面ABCD是菱形, ∠ABC=60º,
所以AB=AD=AC=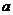 。
(2分)
。
(2分)
在△PAB中,由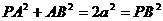 ,
知PA⊥AB。
(5分)
,
知PA⊥AB。
(5分)
同理, PA⊥AD,所以PA⊥平面ABCD。 (7分)
 (II)当点F是棱PE的中点时,有BF∥平面AEC。(8分)
(II)当点F是棱PE的中点时,有BF∥平面AEC。(8分)
取PE的中点F,连结AF,∵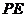 :
: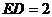 :
: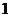 ,
,
∴E为DF的中点。 (10分)
连结BD,交AC于O,连结OE,则有OE∥BF。(12分)
又OE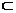 平面AEC,BF
平面AEC,BF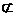 ∥平面AEC,
∥平面AEC,
故BF∥平面AEC。 (14分)
(若从平行探索到F为中点而没有给出证明,扣2分。)
20.(1)解:由题意,可设椭圆的方程为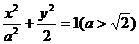 。
。
由已知得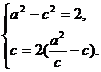
解得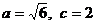 (2分)
(2分)
所以椭圆的方程为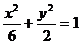 ,离心率
,离心率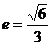 。 (4分)
。 (4分)
(2)解:由(1)可得A(3,0)。
设直线PQ的方程为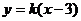 。由方程组
。由方程组
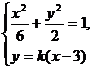
得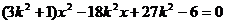 (5分)
(5分)
依题意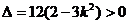 ,得
,得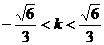 。 (6分)
。 (6分)
设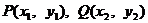 ,则
,则
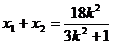 , ①
, ①
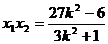 。 ②
。 ②
由直线PQ的方程得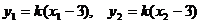 。于是
。于是
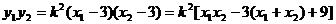 。
③
。
③
∵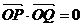 ,∴
,∴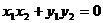 。 ④ (7分)
。 ④ (7分)
由①②③④得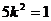 ,从而
,从而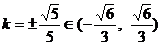 。 (8分)
。 (8分)
所以直线PQ的方程为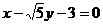 或
或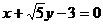 。 (9分)
。 (9分)
(3)证明: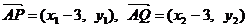 。由已知得方程组
。由已知得方程组
 (10分)
(10分)
注意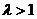 ,解得
,解得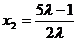 (12分)
(12分)
因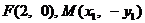 ,故
,故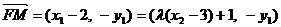
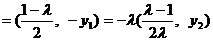 ,而
,而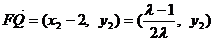 ,
,
所以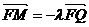 。 (14分)
。 (14分)
21.解:(1)∵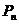 的横坐标构成以
的横坐标构成以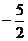 为首项,
为首项,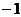 为公差的等差数列
为公差的等差数列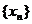 ,
,
∴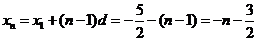 , (2分)
, (2分)
∵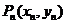 位于函数
位于函数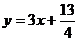 的图像上,
的图像上,
∴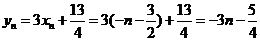 , (3分)
, (3分)
∴点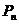 的坐标为
的坐标为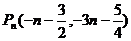 。 (4分)
。 (4分)
(2)据题意可设抛物线 的方程为:
的方程为: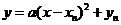 ,
,
即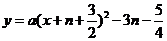 ,
(5分)
,
(5分)
∵抛物线 过点
过点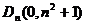 ,
,
∴ ,
,
∴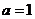 ,∴
,∴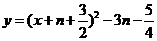 , (6分)
, (6分)
∵过点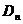 且与抛物线
且与抛物线 只有一个交点的直线即为以
只有一个交点的直线即为以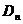 为切点的切线,
为切点的切线,
∴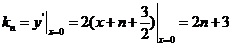 , (7分)
, (7分)
∴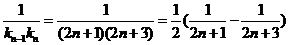 (
(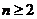 )
)
∴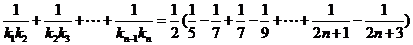
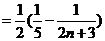
∴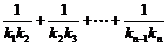
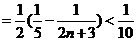 。 (10分)
。 (10分)
(3)∵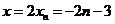 ,
,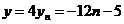
∴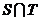 中的元素即为两个等差数列
中的元素即为两个等差数列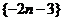 与
与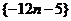 中的公共项,它们组成以
中的公共项,它们组成以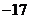 为首项,以
为首项,以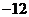 为公差的等差数列,
(11分)
为公差的等差数列,
(11分)
∵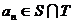 ,且
,且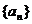 成等差数列,
成等差数列,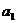 是
是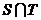 中的最大数,
中的最大数,
∴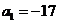 ,其公差为
,其公差为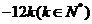 ,
,
10当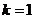 时,
时,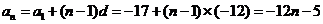 ,
,
此时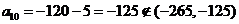 ,∴不满足题意,舍去;(14分)
,∴不满足题意,舍去;(14分)
20当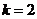 时,
时, ,
,
此时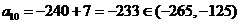 ,
,
∴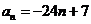 ;
;
30当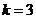 时,
时,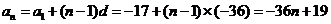 ,
,
此时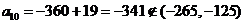 ,∴不满足题意,舍去。(16分)
,∴不满足题意,舍去。(16分)
综上所述所求通项为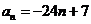 。 (16分)
。 (16分)