
网址:http://www.1010jiajiao.com/paper/timu/5154765.html[举报]
17.(本小题满分12分,第1小问满分5分,第2小问满分7分)
设函数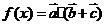 ,其中向量
,其中向量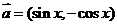 ,
,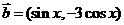 ,
,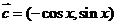 ,
,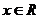 。
。
(Ⅰ)、求函数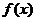 的最大值和最小正周期;
的最大值和最小正周期;
(Ⅱ)、将函数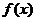 的图像按向量
的图像按向量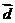 平移,使平移后得到的图像关于坐标原点成中心对称,求长度最小的
平移,使平移后得到的图像关于坐标原点成中心对称,求长度最小的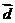 。
。
高考数学第二轮复习模拟试卷答案
一、选择题 (每小题5分,共50分)
D,A,A,D,C,B,C,B,A,A
二、填空题(每小题5分,共30分)
11.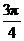 12.
12.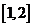 13.
13.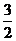 14.
14.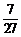 15.1 16.
15.1 16.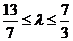
三、解答题(5大题,共70分)
17.解:(Ⅰ)由题意得,f(x)=a.(b+c)=(sinx,-cosx).(sinx-cosx,sinx-3cosx)
=sin2x-2sinxcosx+3cos2x=2+cos2x-sin2x=2+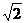 sin(2x+
sin(2x+ ).
).
所以,f(x)的最大值为2+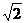 , 最小正周期是
, 最小正周期是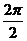 =
=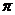 .
.
(Ⅱ)由sin(2x+ )=0得2x+
)=0得2x+ =k.
=k.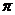 ,即x=
,即x=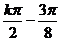 ,k∈Z,
,k∈Z,
于是d=(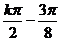 ,-2),
,-2),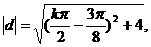 k∈Z.
k∈Z.
因为k为整数,要使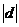 最小,则只有k=1,此时d=(―
最小,则只有k=1,此时d=(―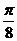 ,―2)即为所求.
,―2)即为所求.
18.设A表示“甲机被击落”这一事件,则A发生只可能在第2回合中发生,而第2回合又只能在第1回合甲失败了才可能进行,用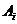 表示第
表示第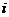 回合射击成功
回合射击成功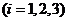 。B表示“乙机被击落”的事件,则
。B表示“乙机被击落”的事件,则
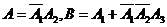
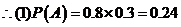
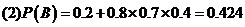 。
。
答:略
19解:
(1)
由已知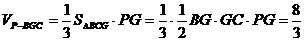 ,∴PG=4.
,∴PG=4.
在平面ABCD内,过C点作CH//EG,交AD于H,连结PH,则∠PCH(或其补角)就是异面直线GE与PC所成的角. 在△PCH中,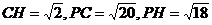 ,由余弦定理得,cos∠PCH=
,由余弦定理得,cos∠PCH=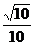 ∴异面直线GE与PC所成的角为arccos
∴异面直线GE与PC所成的角为arccos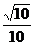
(2)∵PG⊥平面ABCD,PG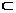 平面PBG ∴平面PBG⊥平面ABCD
平面PBG ∴平面PBG⊥平面ABCD
在平面ABCD内,过D作DK⊥BG,交BG延长线于K,则DK⊥平面PBG
∴DK的长就是点D到平面PBG的距离.
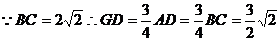 在△DKG,DK=DGsin45°=
在△DKG,DK=DGsin45°=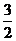
∴点D到平面PBG的距离为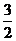 .
.
(3)在平面ABCD内,过D作DM⊥GC,M为垂足,连结MF,又因为DF⊥GC
∴GC⊥平面MFD, ∴GC⊥FM.
由平面PGC⊥平面ABCD,∴FM⊥平面ABCD,∴FM//PG.
由GM⊥MD,得GM=GD.cos45°=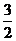 .
.
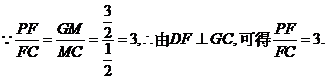
20、(1)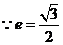 ,
,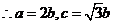 ,将直线
,将直线 的方程
的方程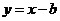 代入到椭圆方程
代入到椭圆方程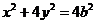 中,得
中,得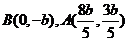 。又
。又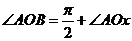 ,
, ,从而由
,从而由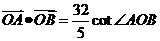 ,得
,得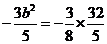
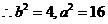 即椭圆的方程为:
即椭圆的方程为: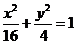
(2) 将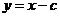 代入到椭圆方程,
代入到椭圆方程,
得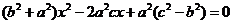
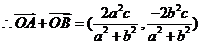 ,
,
故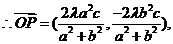
又点 在椭圆上,从而
在椭圆上,从而 ,
,
化简得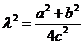 ,设椭圆的离心率为
,设椭圆的离心率为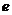 ,
,
则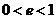 ,且
,且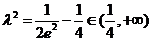 ,故
,故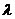 的取值范围为
的取值范围为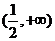
21、(1)当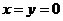 时,
时,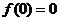 ,再令
,再令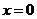 得
得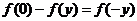 即
即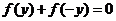
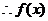 在
在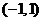 上为为奇函数。
上为为奇函数。
(2)由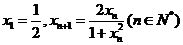 易知:
易知: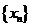 中
中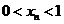 ,
,
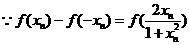 且
且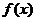 在
在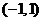 上为奇函数
上为奇函数
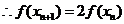 由
由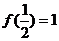 ,
,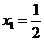
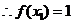
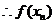 是以1为首项,2为公比的等比数列
是以1为首项,2为公比的等比数列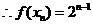
(3)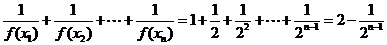
假设存在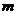 使得
使得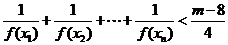 成立,即
成立,即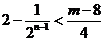 恒成立,
恒成立,
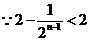
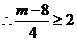
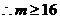
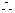 存在自然数
存在自然数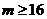 ,使得
,使得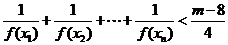 成立,此时最小的自然数
成立,此时最小的自然数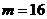 。
。