网址:http://www.1010jiajiao.com/paper/timu/5154806.html[举报]
16、矩形ABCD中,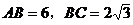 ,沿对角线BD将三角形ABD向上折起,使点A移动到点P,使点P在平面BCD上的射影在DC上(如下图F)。
,沿对角线BD将三角形ABD向上折起,使点A移动到点P,使点P在平面BCD上的射影在DC上(如下图F)。
(I)求证:PD⊥PC;
(II)求二面角P-DB-C的大小;
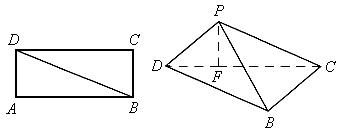 (III)求直线CD与平面PBD所成角的大小。
(III)求直线CD与平面PBD所成角的大小。
 17、已知四棱锥P-ABCD(如图),底面是边长为2的正方形. 侧棱PA⊥底面ABCD,M、N分别为AD、BC的中点. MQ⊥PD于Q,直线PC与平面PBA所成角的正弦值为
17、已知四棱锥P-ABCD(如图),底面是边长为2的正方形. 侧棱PA⊥底面ABCD,M、N分别为AD、BC的中点. MQ⊥PD于Q,直线PC与平面PBA所成角的正弦值为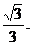
(Ⅰ)求证:平面PMN⊥平面PAD;
(Ⅱ)求PA的长;
(Ⅲ)求二面角P-MN-Q的余弦值.
九、直线、平面、简单几何体参考答案
1、D;2、C;3、B;4、D;5、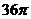 ;6、B;7、A;8、
;6、B;7、A;8、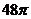 ;9、D;10、
;9、D;10、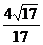 ;
;
11、D;12、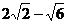
13. (I)证: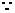 三棱柱
三棱柱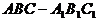 中
中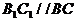 ,
又
,
又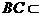 平面
平面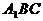 ,
,
且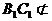 平面
平面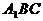 ,
,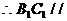 平面
平面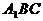
(II)证: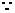 三棱柱
三棱柱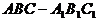 中
中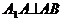 ,
,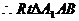 中
中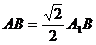
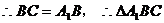 是等腰三角形,
是等腰三角形,
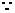 E是等腰
E是等腰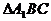 底边
底边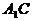 的中点,
的中点,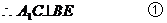
又依条件知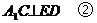 ,且
,且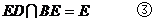
由①,②,③得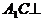 平面EDB
平面EDB
(III)解: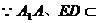 平面
平面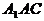 ,且
,且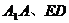 不平行,
不平行,
故延长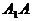 ,ED后必相交,设交点为E,连接EF,如下图
,ED后必相交,设交点为E,连接EF,如下图
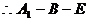 是所求的二面角,依条件易证明
是所求的二面角,依条件易证明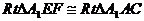
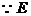 为
为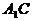 中点,
中点,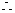 A为
A为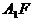 中点,
中点,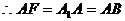
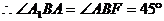 ,
,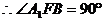 ,
即
,
即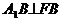
又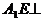 平面EFB,
平面EFB,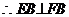 ,
,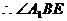 是所求的二面角的平面角
是所求的二面角的平面角
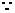 E为等腰直角三角形
E为等腰直角三角形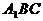 底边中点,
底边中点,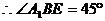
故所求的二面角的大小为
14、解: 以A1B1所在直线为轴,A1D1所在直线为y轴,A1A所在直线为z轴,建立空间直角坐标系。
(1)设E是BD的中点,∵P-ABCD是正四棱锥,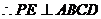 ,
,
又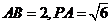 ,
, 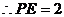 ,
, 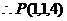 ,
,
∴ = (-2,2,0), = (1,1,2),
∵ .=0,∴ ⊥,即 。
。
(2)设平面PAD的法向量是m = (x,y,z), ∵= (0,2,0) , = (1,1,2) ,
∴ Þ Þ ,
取 得m = (-2,0,1),∴cos<m,n>
= = - ,
得m = (-2,0,1),∴cos<m,n>
= = - ,
 。
。
15.解:如图所示,建立空间直角坐标系,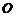 是底面的中心,
是底面的中心,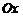 ∥
∥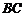 ,
,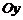 ∥
∥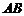 .
.
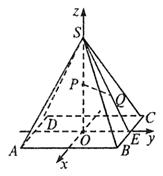 则有关点的坐标为
则有关点的坐标为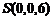 ,
,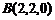 ,
,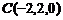 .
.
∵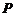 是
是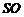 的中点,
的中点,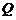 是
是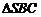 的重心,
的重心,
∴它们的坐标为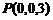 ,
,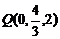 .
.
(1)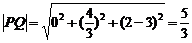 .
.
∴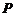 、
、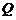 两点间的距离为
两点间的距离为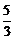 .
.
(2)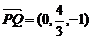 ,
,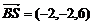 ,设
,设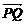 、
、 的夹角为
的夹角为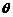 ,
,
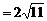 ,
,
∴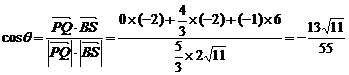 .
.
∴异面直线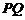 、
、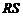 所成角的余弦值为
所成角的余弦值为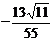 .
.
(3)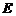 是
是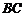 的中点,可以证明直线
的中点,可以证明直线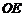 是直线
是直线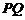 在平面
在平面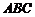 上的射影.
上的射影.
故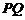 与
与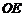 所成角就是
所成角就是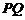 与平面
与平面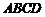 所成的角.点
所成的角.点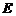 的坐标为(0,2,0)
的坐标为(0,2,0)
∴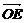 =(0,2,0),
=(0,2,0),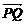 =(0,
=(0,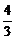 ,-1).
,-1).
设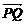 、
、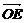 的夹角为
的夹角为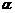 ,则
,则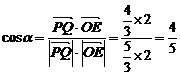 .
.
∴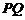 与平面
与平面 所成的角为
所成的角为 .
.
16、(I)证明:∵四边形ABCD为矩形,∴BC⊥CD,DA⊥AB,∵A点移动到了P点
∴PD⊥PB,又∵P点在平面BCD上的射影在CD上,∴过P点作PF⊥CD
∴PF⊥面BCD,∴BC⊥面PCD,∴BC⊥PD,∴PD⊥面PBC, ∴PD⊥PC
(II)解:∵PF⊥面BCD, ∴过点F作FE⊥BD,连结PE
∴∠PEF为二面角P-BD-C的平面角,∵PD⊥PC,∴△CPD为Rt△
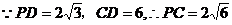 ,
,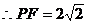
又∵在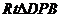 中,
中,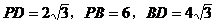 ,∴PE=3
,∴PE=3
 ,
,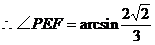
(III)解:过F点作FG⊥PE,由(2)可知FG⊥面PBD,连结GD
∴∠GDF为直线CD与平面PDB所成的角
∵在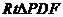 中,
中,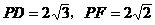 ,∴DF=2
,∴DF=2
∵在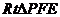 中,
中,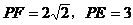 ,
,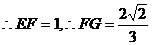 ,
,
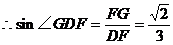 ,
,
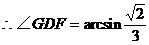
17、解:(I)以A为坐标原点,分别以AB,AD,AP所在的直线为x轴,y轴和z轴,建立空间直角坐标系(图略).
设PA=a,则A(0,0,0),B(2,0,0)C(2,2,0),D(0,2,0)P(0,0,a),
M(0,1,0),N(2,1,0).
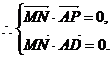 ∴MN⊥平面PAD.
∵MN
∴MN⊥平面PAD.
∵MN 平面PMN,∴平面PMN⊥平面PAD.
平面PMN,∴平面PMN⊥平面PAD.
(II)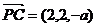 平面PBA的一个法向量为
平面PBA的一个法向量为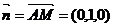 .
.
∵直线PC与平面PBA成角的正弦值为
即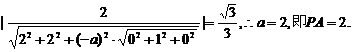
(III)由(I),MN⊥平面PAD,知PM⊥MN,MQ⊥MN,
∴∠PMQ即为二面角P-MN-Q的平面角.
而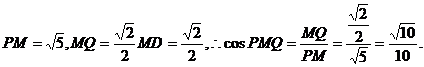
18、解:(1)延长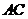 到
到 使
使 ,连结
,连结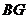 、
、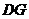 ,
,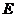 是
是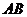 中点,所以
中点,所以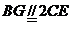 .
.
故直线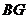 和
和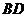 所成的锐角(或直角)就是
所成的锐角(或直角)就是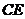 和
和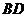 所成的角…2分
所成的角…2分
∵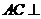 平面
平面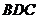 ∴
∴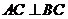 ,又
,又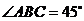 . ∴
. ∴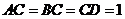 .
.
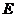 是
是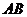 中点,故
中点,故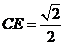 .所以
.所以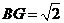 ,又
,又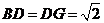 ,因此
,因此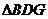 为等边三角形.所以
为等边三角形.所以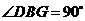 ∴直线
∴直线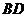 和
和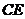 所成的角是
所成的角是
(2)设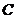 到平面
到平面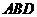 的距离为
的距离为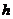 ,则
,则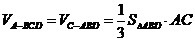
∵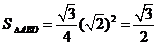 ,
,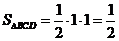 ,
,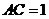 ∴
∴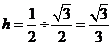
(3)由上可知,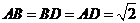 ,又
,又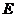 是
是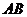 中点,故
中点,故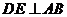 ,
,
由平面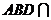 平面
平面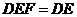 ,∴应
,∴应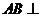 平面
平面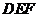
故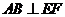 ,即
,即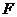 应为过
应为过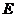 的
的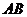 的垂线和
的垂线和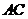 的交点.
的交点.
由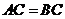 ,所以
,所以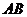 的中垂线过
的中垂线过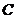 点,即
点,即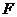 为
为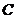 点.
点.
19、解:(I)证明:在△ABC中,AC=BC,M为AB的中点,∴CM⊥AB,
又∵三棱柱ABC-A1B1C1是直三棱柱,
∴平面ABB1A1⊥平面ABC ∴CM⊥平面ABB1A1,
而CM 平面CMD, ∴平面CMD⊥平面ABB1A1
平面CMD, ∴平面CMD⊥平面ABB1A1
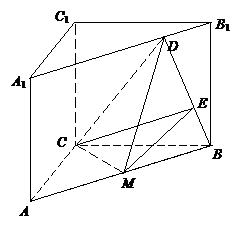 (II)解法一
(II)解法一
过M作ME⊥BD于E,连结CE,
∵CM⊥平面ABB1A1
∴ME是CE在平面ABB1A1上的射影,∴CE⊥BD, 所以∠CEM是二面角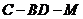 的平面角.
的平面角.
由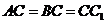 =1,则AB=
=1,则AB=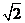 ,
,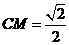 ,
,
取MB的中点F,则BF= ,
,
∴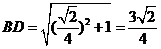
由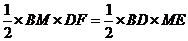 得:
得: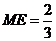
 在Rt△CME中,tan∠CEM=
在Rt△CME中,tan∠CEM=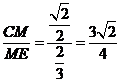
所以∠CEM=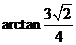
即二面角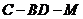 的大小是
的大小是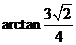
解法二(向量法):以C为原点,分别以CA 、CB、CC1所在直线为x、y、z轴,建立如图所示空间直角坐标系,令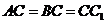 =1,
=1,
则C(0,0,0),A(1,0,0),A1(1,0,1),
B(0,1,0),B1(0,1,1),M(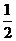 ,
,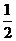 ,0),
,0),
D(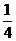 ,
,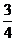 ,1),C1(0,0,1),
,1),C1(0,0,1),
∴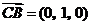 ,
,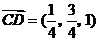 .
.
设平面CBD的法向量为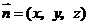 ,则
,则
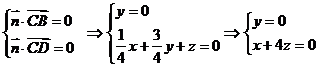 取
取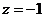 ,则
,则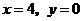 ,∴
,∴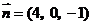 .
.
而平面MBD的法向量是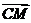 =(
=(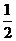 ,
,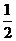 ,0),
,0),
∴cos<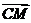 ,
,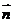 >=
>=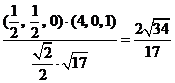 ,即<
,即<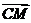 ,
,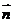 >=
>=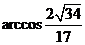
如图可知,二面角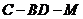 为锐角,∴二面角
为锐角,∴二面角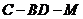 的大小为
的大小为