9..(全国II)如图,平面α⊥平面β,A∈α,B∈β,AB与两平面α、β所成的角分别为和,过A、B分别作两平面交线的垂线,垂足为A′、B′,则AB∶A′B′=
(A)2∶1
(B)3∶1 (C)3∶2
(D)4∶3
解析:连接,设AB=a,可得AB与平面所成的角为
,在,同理可得AB与平面所成的角为,所以,因此在,所以,故选A
[典型考例]
例1.(P75例3) 如图,在五面体ABCDEF中,点O是矩形ABCD的对角线的交点,面CDE是等边三角形,棱 (I)证明平面 (II)设证明平面
(19)本小题考查直线与平面平行、直线与平面垂直等基础知识,考查空间想象能力和推理论证能力。满分12分。
(I)证明:取CD中点M,连结OM。
在矩形ABCD中,
又
则连结EM,于是
四边形EFOM为平行四边形。
又平面CDE,且平面CDE,平面CDE。
(II)证明:连结FM。由(I)和已知条件,在等边中,
且
因此平行四边形EFOM为菱形,从而。
平面EOM,从而
而所以平面
例2. 如图, 在直三棱柱ABC-A1B1C1中,AC=3,BC=4,AA1=4,AB=5点D是AB的中点, (I)求证:AC⊥BC1; (II)求证:AC 1//平面CDB1; (III)设BD1的中点为F,求三棱锥B1-BEF的体积
证:(I)直三棱柱ABC-A1B1C1,底面三边长AC=3,BC=4AB=5,
∴ AC⊥BC,且BC1在平面ABC内的射影为BC,∴ AC⊥BC1;
(II)设CB1与C1B的交点为E,连结DE,∵ D是AB的中点,E是BC1的中点,∴ DE//AC1,
∵ DE平面CDB1,AC1平面CDB1,∴ AC1//平面CDB1;
例2.已知ABCD是上.下底边长分别为2和6,高为的等腰梯形,将它沿对称轴OO1折成直二面角
(Ⅰ)证明:AC⊥BO1;
(Ⅱ)求点O1到平面AOC的距离。
(III)求四面体O1-ACO的体积。
(I)证明 由题设知OA⊥OO1,OB⊥OO1.
所以∠AOB是所折成的直二面角的平面角,
即OA⊥OB. 故可以O为原点,OA、OB、OO1
所在直线分别为轴、y轴、z轴建立空间直角坐标系,
如图3,则相关各点的坐标是A(3,0,0),
B(0,3,0),C(0,1,)O1(0,0,).
从而
所以AC⊥BO1.
例3.如图,在底面为平行四边形的四棱锥中,,平面,且,点是的中点.(Ⅰ)求证:;(Ⅱ)求证:平面;
(Ⅲ)求四面体B-AED的体积。
解:(1)由平面可得PA^AC
又,所以AC^平面PAB,所以
(2)如图,连BD交AC于点O,连EO,则
EO是△PDB的中位线,\EOPB
\PB平面
(3)如图,取AD的中点F,连EF,FO,则EF是△PAD的中位线,\EFPA又平面,\EF^平面
同理FO是△ADC的中位线,\FOAB\FO^AC由三垂线定理可知\ÐEOF是二面角E-AC-D的平面角.又FO=AB=PA=EF\ÐEOF=45°而二面角与二面角E-AC-D互补,故所求二面角的大小为135°.
例4.如图,已知正三棱柱ABC-A1B1C1的侧棱长和底面边长均为1,M是底面BC边上的中点,N是侧棱CC1上的点。(Ⅰ)当B1M⊥AN时,求CN的长度;(Ⅱ)若CN=时,求点B1到平面AMN的距离。

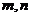 与平面
与平面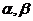 ,有以下四个命题:①若
,有以下四个命题:①若 且
且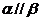 ,则
,则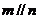 ;②若
;②若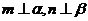 且
且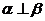 ,则
,则 ;③若
;③若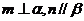 且
且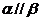 ,则
,则 ;④若
;④若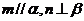 且
且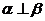 ,则
,则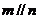 ;其中真命题的序号是
;其中真命题的序号是