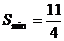2. 对称
P(,)关于点(,)的对称点为:Q(,)
P(,)关于轴的对称点为Q(,)
P(,)关于轴的对称点为Q(,)
P(,)关于的对称点为Q(,)
P(,)关于的对称点为Q(,)
P(,)关于的对称点为Q(,)
P(,)关于的对称点为Q(,)
[典型例题]
[例1] 求点A(,4)关于直线:的对称点。
解:
设A关于的对称点B(,)
∴ B(,)
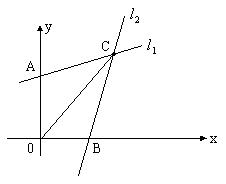
[例2] :,:,求关于对称的直线的方程。
解:
A(0,1)在点,它关于的对称点,B(,)
由两点式 ∴ :
[例3] 光线通过点P(2,3)在直线上反射,反射线过点Q(1,1),求入射光线、反射光线所在直线方程。
解:
(2,3)点关于直线的对称点,(,)
由两点式: 交点(,)
由两点式:
[例4] 正中A(1,1),中心M(5,3),求三边所在直线方程。
解:
∴ AM交于BC于D,M分之比
∴ D=(7,4) ∴ :
设AB、AC为:
∴
[例5] ABC中,A(9,1),B(3,4),内心I(4,1),求C
解:
AI∥轴 ∴ ∴ :
利用三角公式 ∴
∴ : ∴ C(,4)
[例6] 已知中,A(,2)B(6,4)垂心H(5,2),求C
解:
∴ 不存在 ∴
∴ ∴ : C(6,)
[例7] 已知,A(6,3),B(,),C(,)求。
解:
作图,为BC到HC的角 ∴
∴ ∴
[例8] 中,AB、BC、CA边的中点为D(,)E(1,3)F(2,0),求三边所在直线方程。
解:
∴ :即
同理: :
[例9] ,A(,)、B(6,)、C(,),求的角平分线AT所在直线方程。
解:
设斜率为
CA到AT的角等于AT到AB的角
或(舍,结合图形)
∴ :
[例10] 中,A(,)两条中线所在直线方程为,,求BC边所在直线方程。
解:
G(,2) G分之比 ∴ D(,5)
设B(,) ∴ C(,)
∴ 两点式:
[模拟试题]

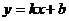 (
(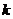 为常数,
为常数,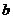 为参数)
为参数)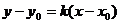 或
或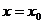 (
(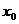 ,
,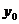 为常数,
为常数,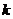 为参数)
为参数)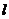 :
: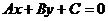 平行直线系
平行直线系 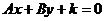 (
(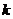 为参数)
为参数)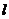 :
: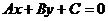 垂直的直线系:
垂直的直线系: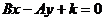 (
(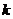 为参数)
为参数) 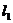 :
: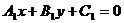 ,
,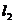 :
: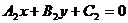
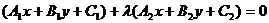 (
(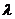 为参数)(不包含
为参数)(不包含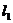 )
)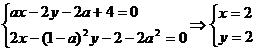
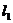 交
交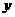 轴于A(0,
轴于A(0,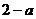 )
) 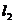 交
交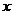 轴于B(
轴于B(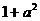 ,0)
,0)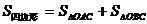
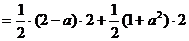
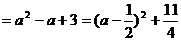
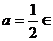 (0,2)时
(0,2)时