
网址:http://www.1010jiajiao.com/paper/timu/5154917.html[举报]
3. 已知直线l过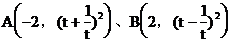 两点,则此直线的斜率和倾斜角分别为(
)
两点,则此直线的斜率和倾斜角分别为(
)
A. 1,135° B.
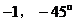
C. 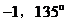 D.
1,45°
D.
1,45°
[试题答案]
1. 答案:D
解析:把直线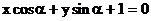 写成
写成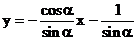
 ,而
,而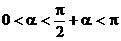
∴直线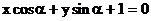 的倾斜角是
的倾斜角是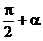
2. 答案: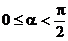 或
或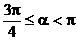
解析: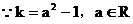
 ,即
,即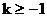
由函数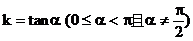 的图象及
的图象及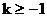 ,知l的倾斜角α的范围是
,知l的倾斜角α的范围是
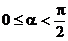 或
或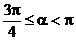
3. 答案:C
解析: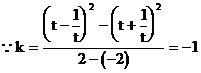
∴直线的倾斜角为135°
4. 答案:D
所求直线的斜率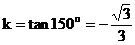
由点斜式得:
即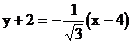
故所求直线方程为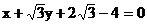
5. 答案:C
解析:直线方程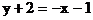 可化为
可化为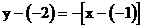
故直线过点( ),斜率为
),斜率为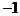
6. 答案:C
解析:直线方程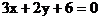 化为斜截式得:
化为斜截式得:
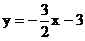 故
故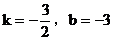
7. 解: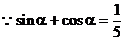
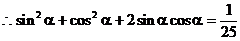
即 
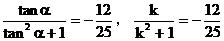
解之,得: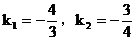
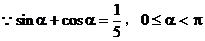
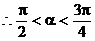
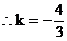 为所求
为所求
8. 解:当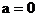 时,
时,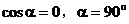 ,该直线的斜率不存在。
,该直线的斜率不存在。
当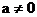 时,
时,
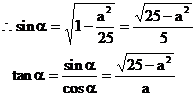
综上所述,当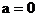 时,所求直线的斜率不存在;
时,所求直线的斜率不存在;
当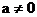 时,所求直线的斜率为
时,所求直线的斜率为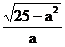 。
。
9. 解:l与线段MN有交点
因为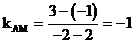 ,所以直线AM的倾斜角为
,所以直线AM的倾斜角为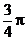 。
。
因为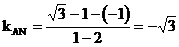 ,所以直线AN的倾斜角为
,所以直线AN的倾斜角为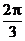 。
。
因为l的倾斜角α的范围是 ,所以l与线段MN有交点。
,所以l与线段MN有交点。
10. 分析:(1)由已知条件求出直线的倾斜角,再求直线的斜率。注意到在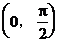 与
与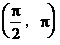 内角的正弦值都取正值,因此用反正弦表示角时,应区分角是锐角还是钝角。
内角的正弦值都取正值,因此用反正弦表示角时,应区分角是锐角还是钝角。
(2)利用方向向量与x轴所夹的最小正角与l的倾斜角相等求解。
解:(1)设直线l的倾斜角为α,则
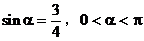
当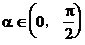 时,
时,

当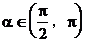 时,
时,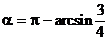

(2)法一:∵v是l的方向向量
∴v∥l
∴v与x轴所夹的最小正角与l的倾斜角α相等,则
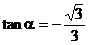
∴l的斜率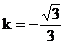 ,倾斜角为
,倾斜角为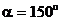
法二:设l的斜率为k,则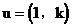 是l的一个方向向量
是l的一个方向向量
由已知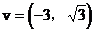 是l的一个方向向量
是l的一个方向向量
∴u∥v,则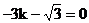
即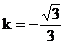
∴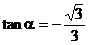 ,倾斜角为
,倾斜角为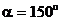
[励志故事]
沉静--思考--判断--成功
从前有位地主巡视谷仓时,不慎将一只名表遗失,因遍寻不获,便定下赏金,要农场上的小孩帮忙寻找,谁能找到手表,奖金500美元。众小孩在重赏之下,无不卖力搜寻,奈何谷仓内到处都是成堆的谷粒和稻草,大家忙到太阳下山仍无所获,结果一个接着一个都放弃了。
只有一个贫穷小孩,为了那笔巨额奖金,仍不死心地寻找。当天色渐黑,众人离去,杂沓人声静下来之后,他突然听到一个奇怪的声音。那声音“滴答、滴答”不停地响着,小孩立刻停下所有的动作,谷仓内更安静了,滴答声也响得更为清晰。小孩循着声音,终于在诺大漆黑的谷仓中找到了那只名贵手表。
“静坐无所为,春来草自青。”
惟有让流水平静下来,太阳和月亮才能在它的表面上显现倒影。
当人沉静下来,才能看出所有干扰清晰思考,蒙蔽真实感情,影响智慧判断,以及阻碍自己找到答案的问题所在。
在自己的内心保留一处梦想可以停驻的宁静地方。