
网址:http://www.1010jiajiao.com/paper/timu/5155019.html[举报]
9.如果命题P: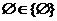 , 命题Q:
, 命题Q: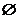
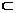
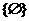 ,那么下列结论不正确的是 ( )
,那么下列结论不正确的是 ( )
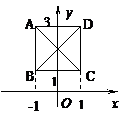 A.“P或Q”为真 B.“P且Q”为假
C.“非P”为假 D.“非Q”为假
A.“P或Q”为真 B.“P且Q”为假
C.“非P”为假 D.“非Q”为假
参 考 答 案(一)
一、选择题(每小题5分,共60分):
(1).D (2).B (3).C (4).C (5).C (6).A (7).C (8).D (9).B (10).A (11). B (12).B
二、填空题(每小题4分,共16分)
(13).3800; (14). 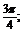 (15). (-∞‚1)∪(3,+∞) ;(16).
(15). (-∞‚1)∪(3,+∞) ;(16).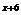 或
或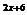 或
或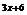 或
或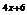 或
或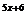
三、解答题(共74分,按步骤得分)
17.解: (1)设 ,由
,由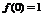 得
得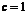 ,故
,故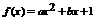 .
.
∵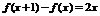 ,∴
,∴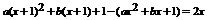 .
.
即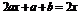 ,所以
,所以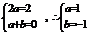 ,∴
,∴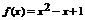 . ……………6分
. ……………6分
(2)由题意得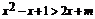 在[-1,1]上恒成立.即
在[-1,1]上恒成立.即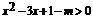 在[-1,1]上恒成立.
在[-1,1]上恒成立.
设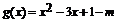 ,其图象的对称轴为直线
,其图象的对称轴为直线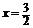 ,所以
,所以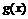 在[-1,1]上递减.
在[-1,1]上递减.
故只需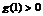 ,即
,即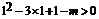 ,解得
,解得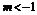 .
……………12分
.
……………12分
18. 解:(1)当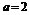 时,
时,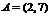 ,
,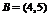 ∴
∴ 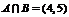 .………4分
.………4分
(2)∵ 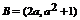 ,
,
当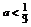 时,
时,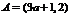 ………………………………5分
………………………………5分
要使
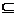 A,必须
A,必须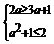 ,此时
,此时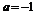 ;………………………………………7分
;………………………………………7分
当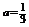 时,A=
时,A=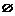 ,使
,使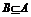 的
的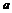 不存在;……………………………………9分
不存在;……………………………………9分
当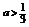 时,A=(2,3
时,A=(2,3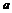 +1)
+1)
要使
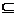 A,必须
A,必须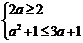 ,此时1≤
,此时1≤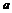 ≤3.……………………………………11分
≤3.……………………………………11分
综上可知,使
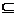 A的实数
A的实数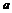 的取值范围为[1,3]∪{-1}……………………………12分
的取值范围为[1,3]∪{-1}……………………………12分
19.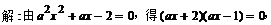
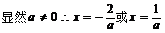 ……4分
……4分
∵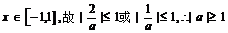 ……6分
……6分

∴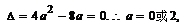 ……10分
……10分
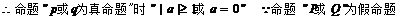
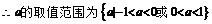 ……12分
……12分
20.解: (1)设任意实数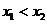 ,则
,则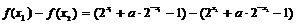
=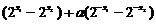 =
=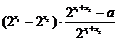 ……………4分
……………4分
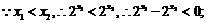
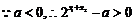 .
.
又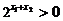 ,∴
,∴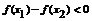 ,所以
,所以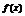 是增函数.
……………7分
是增函数.
……………7分
(2)当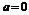 时,
时,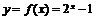 ,∴
,∴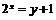 , ∴
, ∴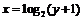 ,
,
y=g(x)= log2(x+1). ………………………12分
21.解:(1)显然函数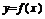 的值域为
的值域为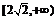 ; ……………3分
; ……………3分
(2)若函数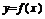 在定义域上是减函数,则任取
在定义域上是减函数,则任取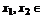
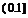 且
且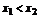 都有
都有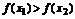 成立,
成立,
即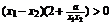 ,只要
,只要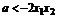 即可, …………………………5分
即可, …………………………5分
由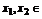
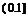 ,故
,故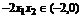 ,所以
,所以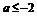 ,
,
故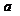 的取值范围是
的取值范围是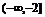 ;
…………………………7分
;
…………………………7分
解法二:∵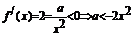 而
而 ∴
∴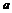 ≤
≤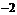
(3)当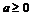 时,函数
时,函数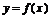 在
在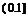 上单调增,无最小值,
上单调增,无最小值,
当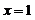 时取得最大值
时取得最大值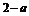 ;
;
由(2)得当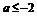 时,函数
时,函数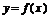 在
在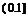 上单调减,无最大值,
上单调减,无最大值,
当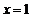 时取得最小值
时取得最小值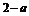 ;
;
当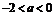 时,函数
时,函数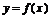 在
在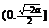 上单调减,在
上单调减,在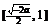 上单调增,无最大值,
上单调增,无最大值,
当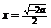 时取得最小值
时取得最小值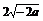 .
…………………………12分
.
…………………………12分
22.解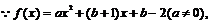
(1)当a=2,b=-2时, 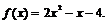 ……………………2分
……………………2分
设x为其不动点,即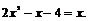
则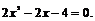
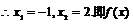 的不动点是-1,2. …………4分
的不动点是-1,2. …………4分
(2)由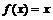 得:
得: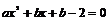 . 由已知,此方程有相异二实根,
. 由已知,此方程有相异二实根,
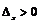 恒成立,即
恒成立,即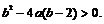 即
即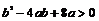 对任意
对任意 恒成立.
恒成立.
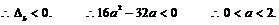 ……………………8分
……………………8分
(3)设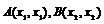 ,
,
直线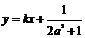 是线段AB的垂直平分线, ∴
是线段AB的垂直平分线, ∴ 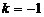 ……………10分
……………10分
记AB的中点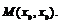 由(2)知
由(2)知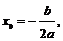
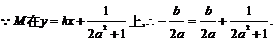 ……………………12分
……………………12分
化简得: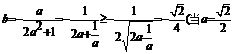 时,等号成立).
时,等号成立).
即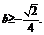 …………………………………………14分
…………………………………………14分