
网址:http://www.1010jiajiao.com/paper/timu/5155063.html[举报]
3、在△ABC中,角A、B、C的对边分别为a、b、c,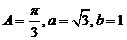 则c=( )
则c=( )
A)1
B)2
C)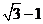 D)
D)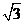
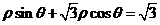 。
。
参考答案:
|
题号 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
|
答案 |
C |
D |
B |
C |
C |
A |
C |
C |
B |
B |
D |
B |
13、2008; 14、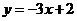 或
或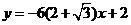 或
或 ;
;
15、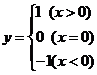 ; 16、
; 16、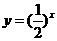 或
或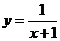
17、解:(1)向量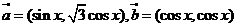 ,若
,若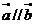 ,则
,则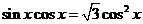 ,∵
,∵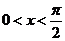 ,∴cosx≠0,∴
,∴cosx≠0,∴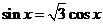 ,∴
,∴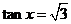 。
。
(2)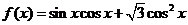

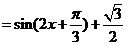 ,
,
∵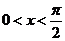 ∴
∴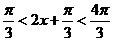 ,因此当
,因此当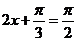 ,
,
即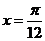 时,
时,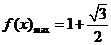 。
。
18、解:(1) 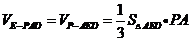
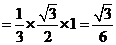
(2) 点E为BC的中点时, EF∥平面PAC。
证明如下:∵BE=CE,BF=PF ∴EF∥PC
又EF在平面PAC外,PC在平面PAC内,所以EF∥平面PAC
(3) ∵PA=AB,BF=PF ∴AF⊥PB ∵PA⊥平面ABCD ∴PA⊥BC
又BC⊥AB ∴BC⊥平面PAB 而AF在平面PAB内,∴AF⊥BC
 ∵BC、PB是平面PBC内的两条相交直线 ∴AF⊥平面PBC
∵BC、PB是平面PBC内的两条相交直线 ∴AF⊥平面PBC
∵无论点E在BC边的何处,PE都在平面PBC内 ∴PE⊥AF
19、解:(Ⅰ)如果按性别比例分层抽样,应抽男生3人,女生5人。
(Ⅱ)(1)在该班随机调查一位同学,由表中可以看出,数学和物理分数均为优秀的人数是3人,所求的概率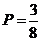 。
。
(2) 变量y与x的相关系数是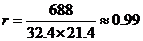 。可以看出,
。可以看出,
物理与数学成绩是高度正相关,或以数学成绩x为横坐标,物理
成绩y为纵坐标做散点图如下:
从散点图可以看出这些点大致分布在一条直线附近,并且在逐步
上升,故物理与数学成绩是高度正相关。
设y与x线性回归方程是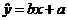 ,根据所给的数据,可以计算
,根据所给的数据,可以计算
出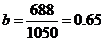 ,
,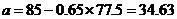 ,
,
所以y与x回归方程是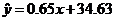 。
。
20、解答:(1)圆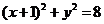 的圆心为C(-1,0),半径
的圆心为C(-1,0),半径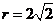 ,
,
∵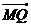 .
.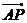 =0,
=0,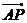 =2
=2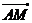 ∴MQ⊥AP,点M是AP的中点,即QM是AP的中垂线 ,连结AQ,则|AQ|=|QP|,
∴MQ⊥AP,点M是AP的中点,即QM是AP的中垂线 ,连结AQ,则|AQ|=|QP|,
∴|QC|+|QA|=|QC|+|QP|=|CP|=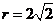 ,又|AC|=2<
,又|AC|=2<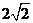 ,
,
根据椭圆的定义,点Q的轨迹是以C(-1,0),A(1,0)为焦点,长轴长为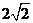 的椭圆,
的椭圆,
由c=1,a= ,得b2=1,因此点Q的轨迹方程为
,得b2=1,因此点Q的轨迹方程为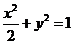 。
。
(2)设F(x1,y1),H(x2,y2),则由 ,消去y得
,消去y得
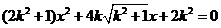 ,△=8k2>0,∴k≠0。
,△=8k2>0,∴k≠0。
∴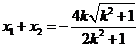 ,
,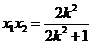 ,∴
,∴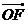 .
.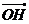 =
=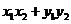
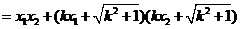
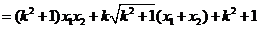
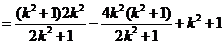
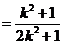 ,由已知
,由已知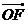 .
.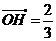 ,得
,得
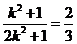 ,∴
,∴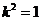 。
。
∵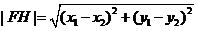
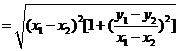
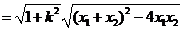
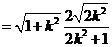 。又点O到直线FH的距离d=1,
。又点O到直线FH的距离d=1,
∴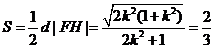
21、解:(1) 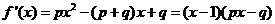 , ∵p>q>0 ∴
, ∵p>q>0 ∴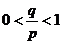 .
.
令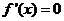 ,得
,得 或
或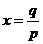 ,列表如下:
,列表如下:
|
x |
(-∞, 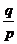 ) ) |
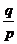 |
(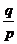 ,1) ,1) |
1 |
(1,+
∞) |
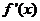 |
+ |
0 |
- |
0 |
+ |
|
f(x) |
↑ |
极大值 |
↓ |
极小值 |
↑ |
由上表可知,x=1时,f(x)取得极小值,因此a1=1。
(2) 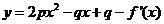
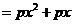 ,
,
∵点(n,2Sn)(n∈N*)均在函数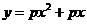 的图象上, ∴
的图象上, ∴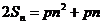 ,
,
由于a1=1,所以2a1=2p,得p=1,∴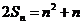 ,又
,又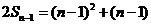 ,
,
上面两式相减,得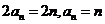 。
。
(3)由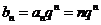 ,所以
,所以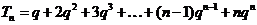 ,
,
由题设p>q>0,而p=1,故q≠1, 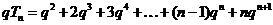 ,
,
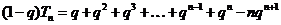
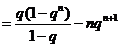 ,
,
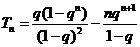 。
。
22、A、选修4-1:几何证明选讲
解:(1)连结OC,∴∠OAC=∠OCA,又∵CA是∠BAF的角平分线,∴∠OAC=∠FAC,
∴∠FAC∠ACO, ∴OC∥AD,∵CD⊥AF,∴CD⊥OC,即DC是⊙O的切线。
(2)连结BC,在Rt△ACB中,CM⊥AB,∴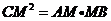 ,又∵DC是⊙O的切线,
,又∵DC是⊙O的切线,
∴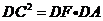 ,易知
,易知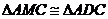 ,∴DC=CM,∴AM.MB=DF.DA
,∴DC=CM,∴AM.MB=DF.DA
B、选修4-4:坐标系与参数方程
解:(1)圆锥曲线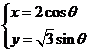 化为普通方程
化为普通方程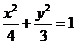 ,
,
所以F1(-1,0),F2(1,0),则直线AF2的斜率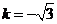 ,于是经过点F1垂直于直线AF2的直线l的斜率
,于是经过点F1垂直于直线AF2的直线l的斜率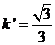 ,直线l的倾斜角是30°,所以直线l的参数方程是
,直线l的倾斜角是30°,所以直线l的参数方程是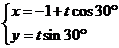 (t为参数),即
(t为参数),即 (t为参数),
(t为参数),
(2)直线AF2的斜率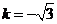 ,倾斜角是120°,设
,倾斜角是120°,设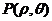 是直线AF2上任一点,
是直线AF2上任一点,
则 ,
,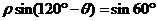 ,则
,则