网址:http://www.1010jiajiao.com/paper/timu/5155088.html[举报]
1
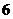 个人坐在一排
个人坐在一排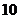 个座位上,问(1)空位不相邻的坐法有多少种?(2)
个座位上,问(1)空位不相邻的坐法有多少种?(2) 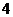 个空位只有
个空位只有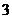 个相邻的坐法有多少种?(3)
个相邻的坐法有多少种?(3) 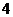 个空位至多有
个空位至多有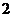 个相邻的坐法有多少种?
个相邻的坐法有多少种?
2 有
有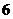 个球,其中
个球,其中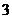 个黑球,红、白、蓝球各
个黑球,红、白、蓝球各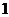 个,现从中取出
个,现从中取出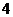 个球排成一列,共有多少种不同的排法?
个球排成一列,共有多少种不同的排法?
3 求
求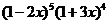 展开式中按
展开式中按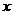 的降幂排列的前两项
的降幂排列的前两项
4 用二项式定理证明:
用二项式定理证明: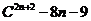 能被
能被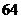 整除
整除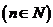

5 求证:
求证: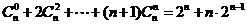

6 (1)若
(1)若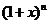 的展开式中,
的展开式中,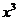 的系数是
的系数是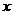 的系数的
的系数的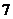 倍,求
倍,求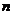 ;
;
(2)已知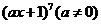 的展开式中,
的展开式中, 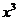 的系数是
的系数是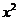 的系数与
的系数与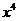 的系数的等差中项,求
的系数的等差中项,求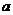 ;
;
(3)已知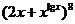 的展开式中,二项式系数最大的项的值等于
的展开式中,二项式系数最大的项的值等于 ,求
,求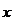

(数学选修2-3) 第一章 计数原理
参考答案
[提高训练C组]
一、选择题
1 B
B 
2 D 男生
D 男生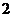 人,女生
人,女生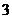 人,有
人,有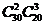 ;男生
;男生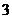 人,女生
人,女生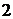 人,有
人,有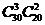
共计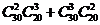
3 A 甲得
A 甲得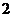 本有
本有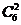 ,乙从余下的
,乙从余下的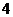 本中取
本中取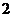 本有
本有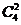 ,余下的
,余下的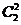 ,共计
,共计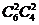
4 B 含有
B 含有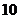 个元素的集合的全部子集数为
个元素的集合的全部子集数为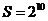 ,由
,由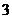 个元素组成的子集数
个元素组成的子集数
为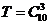 ,
,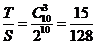
5 A
A 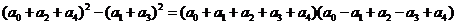
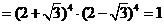
6 D 分三种情况:(1)若仅
D 分三种情况:(1)若仅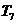 系数最大,则共有
系数最大,则共有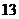 项,
项,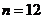 ;(2)若
;(2)若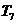 与
与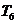 系数相等且最大,则共有
系数相等且最大,则共有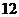 项,
项,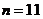 ;(3)若
;(3)若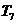 与
与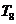 系数相等且最大,则共有
系数相等且最大,则共有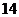 项,
项,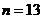 ,所以
,所以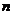 的值可能等于
的值可能等于
7 D 四个点分两类:(1)三个与一个,有
D 四个点分两类:(1)三个与一个,有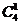 ;(2)平均分二个与二个,有
;(2)平均分二个与二个,有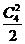
共计有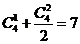
8 D 复数
D 复数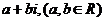 为虚数,则
为虚数,则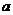 有
有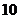 种可能,
种可能,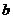 有
有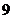 种可能,共计
种可能,共计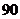 种可能
种可能
二、填空题
1
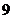 分三类:第一格填
分三类:第一格填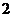 ,则第二格有
,则第二格有 ,第三、四格自动对号入座,不能自由排列;
,第三、四格自动对号入座,不能自由排列;
第一格填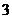 ,则第三格有
,则第三格有 ,第一、四格自动对号入座,不能自由排列;
,第一、四格自动对号入座,不能自由排列;
第一格填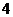 ,则第撕格有
,则第撕格有 ,第二、三格自动对号入座,不能自由排列;
,第二、三格自动对号入座,不能自由排列;
共计有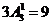
2
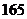
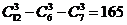
3
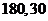
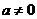 ,
,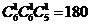 ;
;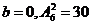
4
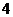
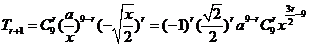 ,令
,令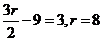

5
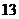

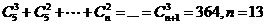
6
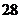
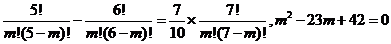
而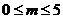 ,得
,得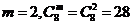
7
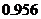
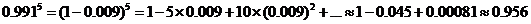
8
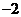 设
设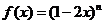 ,令
,令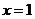 ,得
,得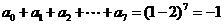
令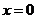 ,得
,得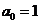 ,
,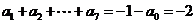
三、解答题
1 解:
解: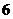 个人排有
个人排有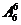 种,
种, 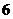 人排好后包括两端共有
人排好后包括两端共有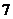 个“间隔”可以插入空位
个“间隔”可以插入空位
(1)空位不相邻相当于将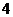 个空位安插在上述
个空位安插在上述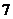 个“间隔”中,有
个“间隔”中,有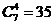 种插法,
种插法,
故空位不相邻的坐法有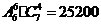 种
种
(2)将相邻的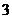 个空位当作一个元素,另一空位当作另一个元素,往
个空位当作一个元素,另一空位当作另一个元素,往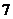 个“间隔”里插
个“间隔”里插
有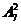 种插法,故
种插法,故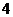 个空位中只有
个空位中只有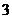 个相邻的坐法有
个相邻的坐法有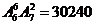 种
种
(3) 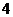 个空位至少有
个空位至少有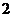 个相邻的情况有三类:
个相邻的情况有三类:
①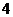 个空位各不相邻有
个空位各不相邻有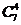 种坐法;
种坐法;
②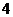 个空位
个空位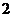 个相邻,另有
个相邻,另有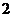 个不相邻有
个不相邻有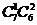 种坐法;
种坐法;
③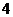 个空位分两组,每组都有
个空位分两组,每组都有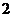 个相邻,有
个相邻,有 种坐法
种坐法
综合上述,应有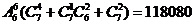 种坐法
种坐法
2 解:分三类:若取
解:分三类:若取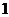 个黑球,和另三个球,排
个黑球,和另三个球,排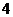 个位置,有
个位置,有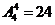 ;
;
若取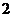 个黑球,从另三个球中选
个黑球,从另三个球中选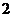 个排
个排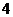 个位置,
个位置,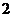 个黑球是相同的,
个黑球是相同的,
自动进入,不需要排列,即有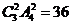 ;
;
若取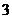 个黑球,从另三个球中选
个黑球,从另三个球中选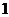 个排
个排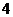 个位置,
个位置,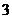 个黑球是相同的,
个黑球是相同的,
自动进入,不需要排列,即有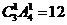 ;
;
所以有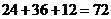 种
种
3 解:
解: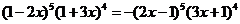
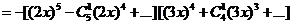
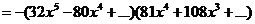
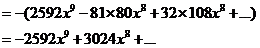
4 解:
解: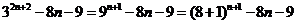
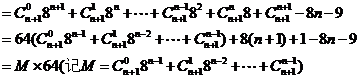
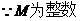 ,
,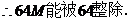
5 证明:
证明: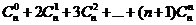

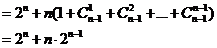
6 解:(1)
解:(1)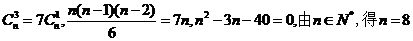 ;
;
(2)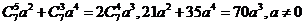
得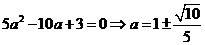 ;
;
(3)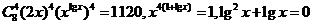
得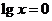 ,或
,或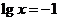
所以