[例4]如图，在多面体ABCDEF中，已知ABCD是边长为3的正方形，EF∥AB，EF与面AC的距离是2，且EF＝，则该多面体的体积为(　　 ) A．　　B．5　　　 C．6　　　 D． [方法1](分割法+特殊化)：V＝VE-AMND +VEMN-FBC ＝…＝； [方法2](补形法+特殊化)：V＝VGAD-FBC－VE-ADG ＝…＝； [方法3](放缩法)：V＞VE-ABCD ＝ .2.32——青夏教育精英家教网—

精英家教网> 试卷> 高考数学考前指导练习(小题) 高考数学“小题”是指选择题、填空题，属于客观性试题。一方面具有题小、量大、基础、灵活、答案唯一(开放型填空题除外)等特点；另一方面具有比较明显的学科特点，即概念性强，量化突出，充满思辨性，形数兼备，解法多样化；是考查知识掌握程度和区分考生的能力层次、思维品质的重要题型，其分值约占全卷分值的53%(选择题33%，填空题20%)。用简缩的思维，快速、准确、灵活地得知结果，是每个考生希望达到的境界。解题的基本原则：小题不能大做，消除隐形失分。解题的基本策略：要充分利用题设 > 题目详情

网址：http://www.1010jiajiao.com/paper/timu/5155151.html[举报]

[例4]如图，在多面体ABCDEF中，已知ABCD是边长为3的正方形，EF∥AB，EF与面AC的距离是2，且EF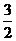＝，则该多面体的体积为(　　 )

A．　　B．5　　　 C．6　　　 D．

[方法1](分割法+特殊化)：V＝V_E_-AMND+V_EMN_-FBC＝…＝；

[方法2](补形法+特殊化)：V＝V_GAD_-FBC－V_E_-ADG＝…＝；

[方法3](放缩法)：V＞V_E_-ABCD＝ .2.3²＝ 6，故选D。

『类题1』函数f (x) ＝ Msin(ωx+φ)　 (ω＞0) 在区间 [a，b] 上是增函数，且f (a) ＝－M，f (b) ＝ M，则函数g (x) ＝ Mcos (ωx+φ)在区间 [a，b] 上(　　 )

A．是增函数　　 B．是减函数　　 C．可以取得最大值M　　 D．可以取得最小值－M

[方法1](换元法)：令t＝ωx+φ，x∈[a，b]，设t∈[－π/2，π/2]即可排除A、B、D，选C；

[方法2](特殊化)：取M＝ω＝1，φ＝0，且a ＝－π/2，b ＝π/2，满足题设；

[方法3](特殊化+图解)：作出f (x) ＝sinx、g (x) ＝ cos x　 x∈[－π/2，π/2] 即知；

[方法4](分析法)：　由题设可知 [f (x)]²+ [ g (x)]²＝ M²，且f (a) ＝－M，f (b) ＝ M，

得g (a) ＝ g (b) ＝ 0，排除A、B，又f (x)在 [a，b] 上递增，从而g(x)≥0，排除D，故选C。

[小结]多种手段协同作战，如虎添翼，巧夺天工。

『类题2』椭圆的焦点F₁、F₂，点P是椭圆上动点，当∠F₁PF₂为钝角时，点P的横坐标的取值范围是　　　　　　　　　　 .

[方法1]用焦半径公式，|PF₁| ＝3 + x₀，|PF₂| ＝3 － x₀，代入 |PF₁|²+ |PF₂|²＜ |F₁F₂|²得x₀²＜，从而x₀∈(－，)；

[方法2]用焦半径公式+特殊化，|PF₁| ＝3 + x₀，|PF₂| ＝3 － x₀，代入 |PF₁|²+ |PF₂|²＝ |F₁F₂|²得x₀²＝，从而x_P∈(－，)；

[方法3]用焦半径公式+椭圆定义，|PF₁|²+ |PF₂|²＜20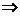(|PF₁|+ |PF₂|)²＜20 +2|PF₁|.|PF₂| 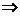|PF₁|.|PF₂| ＝ 9 － x₀²＞8　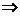x₀²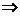＜ x₀∈(－，)；

[方法4]构造圆x²+y²＝5，与椭圆联立求得交点x₀²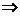＝ x₀∈(－，)；

[方法5]特殊化+椭圆定义+面积公式，20＝|PF₁|²+ |PF₂|²＝(|PF₁|+ |PF₂|)²－2|PF₁|.|PF₂|，　　　　　 S_△＝ |PF₁|.|PF₂|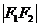＝ .|y|，代入上式得|y| ＝，

代入椭圆方程得x²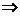＝ x₀∈(－，)；

[方法6]参数法，设P(3cosθ，2sinθ)，代入 |PF₁|²+ |PF₂|²＜ |F₁F₂|²得 cos²θ＜，得x₀＝ 3 cosθ∈(－，)；

『开放(Ⅰ)』椭圆的焦点F₁、F₂，点P为椭圆上动点，连结PF₁、PF₂，试尽可能多地写出一些正确的论断：　　　　　　　　　　　　　　

(1)a ＝3，b ＝2，c ＝，e ＝，p ＝； (2)焦点(±，0)，准线x ＝±；

(3)|PF₁|+ |PF₂|＝ 6；　　　　　　　　　　　　(4)P(x₀，y₀)；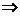

(5)|PF₁| ＝＝ 3 + x₀，|PF₂| ＝＝ 3 － x₀；

(6)cos∠F₁PF₂＝－1；　　　　　　　　　　　(7)S_△＝ b².tan；

(8)PF₁⊥x轴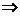| PF₁| ＝；　　　　　　　　　　 (9)S_椭圆＝πab；

(10)a －c≤| PF|≤a+c且b²≤| PF₁|+| PF₂|≤a²；

『开放(Ⅱ)』椭圆的焦点F₁、F₂，点P为椭圆上动点，当∠F₁PF₂＝90°时，写出三个相应的正确结论　　　　　　　　　　　　　　　　 .

(11)P(，±)或(－，±)；　　　 (12)| PF₁| ＝2或4；

(13)P点到两焦点的距离之比为2：1；　　　　 (14)P点到两准线的距离之比为2：1；

(15)P点到原点的距离为；　　　　　　　　 (16)S_△F_1PF₂＝ 4；

『开放(Ⅲ)』在(Ⅰ)的条件下，当P点在何处时，提出问题：

(17)S_△F_1PF₂最大；　　　　　　　　　　　　　 (18)∠F₁PF₂最大；

(19)| PF₁|.| PF₂| 最大？最小？　　　　　　　 (20)∠F₁PF₂为直角？锐角？钝角？

(21)S_△＜4；
题目来源：高考数学考前指导练习(小题) 高考数学“小题”是指选择题、填空题，属于客观性试题。一方面具有题小、量大、基础、灵活、答案唯一(开放型填空题除外)等特点；另一方面具有比较明显的学科特点，即概念性强，量化突出，充满思辨性，形数兼备，解法多样化；是考查知识掌握程度和区分考生的能力层次、思维品质的重要题型，其分值约占全卷分值的53%(选择题33%，填空题20%)。用简缩的思维，快速、准确、灵活地得知结果，是每个考生希望达到的境界。解题的基本原则：小题不能大做，消除隐形失分。解题的基本策略：要充分利用题设

题目所在试卷参考答案：

⑤有一组对角相等的四边形

参考答案：

1	2	3	4	5	6	7	8	9	10	11	12
A	A	D	D	A	A	C	C	C	A	C	B

13、155　　　 14、3　　　　　 15、(1)(2)(3)　　　　 16、500　　　　　 17、x轴，－3－log₂x 　

或 y轴， 3+log₂(－x)　　　　或原点，－3－log₂(－x)　　　　或y＝x，　 2^x^－3　　

18、　　　 19、①③④　　　　 20、②③⑤

试卷相关题目

练习册

高中

初中

小学