
网址:http://www.1010jiajiao.com/paper/timu/5155226.html[举报]
14.考察下列一组不等式: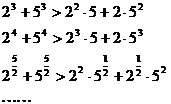 将上述不等式在左右两端视为两项和的情况下加以推广,使以上的不等式成为推广不等式的特例,则推广的不等式为 .
将上述不等式在左右两端视为两项和的情况下加以推广,使以上的不等式成为推广不等式的特例,则推广的不等式为 .
参考答案
|
题号 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
|
答案 |
B |
B |
C |
C |
A |
D |
D |
A |
9.85 10.②④ 11.
①②④ 12. 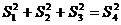
13. 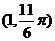 14.
14. 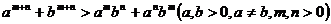
15.解:(I)∵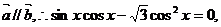 ……………………3分
……………………3分
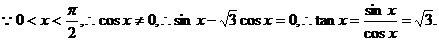 …6分
…6分
(Ⅱ)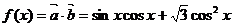 …………………………8分
…………………………8分
=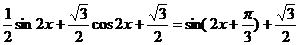 .………………10分
.………………10分
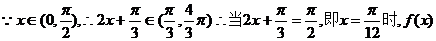
|
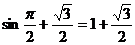 ………………………………12分
………………………………12分
16.解法1:(I)当点E为BC的中点时,
EF与平面PAC平行.∵在△PBC中,
E、F分别为BC、PB的中点,
∴EF//PC 又EF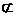 平面PAC,
平面PAC,
而PC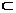 平面PAC ∴EF//平面PAC.…4分
平面PAC ∴EF//平面PAC.…4分
(II)证明:∵PA⊥平面ABCD,BE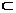 平面ABCD,
平面ABCD,
∴EB⊥PA.又EB⊥AB,AB∩AP=A,AB,AP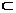 平面PAB,
平面PAB,
∴EB⊥平面PAB,
又AF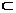 平面PAB,∴AF⊥BE.
平面PAB,∴AF⊥BE.
又PA=AB=1,点F是PB的中点,∴AF⊥PB,……………………4分
又∵PB∩BE=B,PB,BE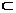 平面PBE,∴AF⊥平面PBE.
平面PBE,∴AF⊥平面PBE.
∵PE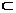 平面PBE,∴AF⊥PE.……………………8分
平面PBE,∴AF⊥PE.……………………8分
(Ⅲ)过A作AG⊥DE于G,连PG,又∵DE⊥PA,则DE⊥平面PAG,
于是,平面PAG⊥平面PDE,它们的交线是PG,过A作AM⊥PG,垂足为M,则AM⊥平面PDE,即PA在平面PDE的射影是PM,所以PA与平面PDE所成的角是∠APG=45°.
∴在RtPAG中,PA=AG=1,∴DG=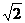 ,………………10分
,………………10分
设BE=x,∵△AGE≌△ABE,则GE=x,CE=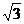 -x,
-x,
|
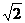 +x)2=(
+x)2=(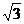 -x)2+12,得BE=x=
-x)2+12,得BE=x=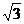 -
-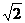 .……12分
.……12分
解法二: (II)建立图示空间直角坐标系,
则P(0,0,1),B(0,1,0),
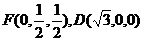 设
设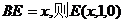
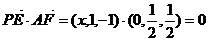 ∴AF⊥PE …8分
∴AF⊥PE …8分
(Ⅲ)设平面PDE的法向量为

而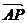 =(0,0,1)依题意PA与平面PDE所成角为45°,
=(0,0,1)依题意PA与平面PDE所成角为45°,
所以sin45°=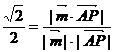 ,
,
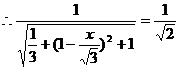 ,
,
得BE=x=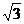 -
-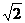 ,或BE=x=
,或BE=x=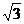 +
+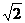 (舍).……………………12分
(舍).……………………12分
17.解:(I)应选女生25×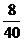 =5(个),男生15×
=5(个),男生15×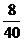 =3(个),可以得到不同的样本个数是
=3(个),可以得到不同的样本个数是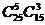 .……4分(II)(1)这8位同学中恰有3位同学的数学和物理分数均为优秀,则需要先从物理的4个优秀分数中选出3个与数学优秀分数对应,种数是
.……4分(II)(1)这8位同学中恰有3位同学的数学和物理分数均为优秀,则需要先从物理的4个优秀分数中选出3个与数学优秀分数对应,种数是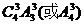 ,然后剩下的5个数学分数和物理分数任意对应,种数是
,然后剩下的5个数学分数和物理分数任意对应,种数是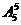 。根据乘法原理,满足条件的种数是
。根据乘法原理,满足条件的种数是 …………………………………………6分
…………………………………………6分
这8位同学的物理分数和数学分数分别对应的种数共有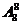 .…………7分
.…………7分
故所求的概率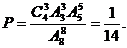 ………………………………10分
………………………………10分
|
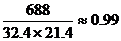 .可以看出,物理与数学成绩是高度正相关.若以数学成绩x为横坐标,
.可以看出,物理与数学成绩是高度正相关.若以数学成绩x为横坐标,
物理成绩y为纵坐标做散点图如下
从散点图可以看出这些点大至分布
在一条直线附近,并且在逐步上升,
故物理与数学成绩是高度正相关.
………………………………12分
设y与x线性回归方程y=bx+a、
根据所给的数据,可以计算出
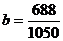 =0.65,a=85-0.65×77.5=34.63,
=0.65,a=85-0.65×77.5=34.63,
所以y与x的回归方程是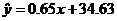 .……………………14分
.……………………14分
18. 解:(1)由题意MQ是线段AP的垂直平分线,于是
|CP|=|QC|+|QP|=|QC|+|QA|=2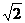 >|CA|=2,于是点 Q的轨迹是以点C,A为焦点,半焦距c=1,长半轴a=
>|CA|=2,于是点 Q的轨迹是以点C,A为焦点,半焦距c=1,长半轴a=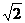 的椭圆,短半轴
的椭圆,短半轴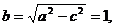
点Q的轨迹E方程是: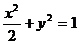 .…………………………4分
.…………………………4分
(2)设F(x1,y1)H(x2,y2),则由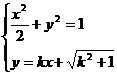 ,
,
消去y得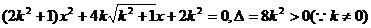
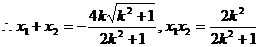 …………………………6分
…………………………6分
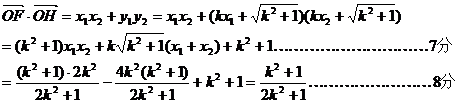
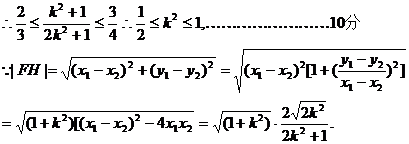
又点O到直线FH的距离d=1,
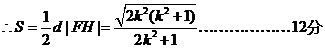
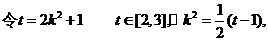

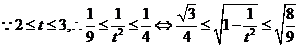

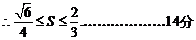
19. 解:(I)解: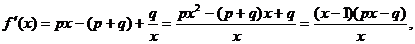
令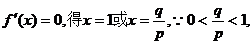
当x=变化时,f′(x),f(x)的变化情况如下表:
|
|
(0,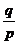 ) ) |
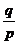 |
(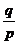 ,1) ,1) |
1 |
(1,+∞) |
|
f′(x) |
+ |
0 |
- |
0 |
+ |
|
f(x) |
 |
极大值 |
 |
极小值 |
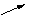 |
所以f(x)在x=1处取得最小值,即a1=1.………………………………5分
(II)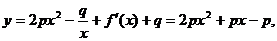
 ,
,
由于a1=1,所以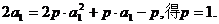 ………6分
………6分
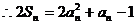 ……………………①.………………………………8分
……………………①.………………………………8分
又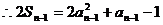 …………………………②。
…………………………②。
①-②得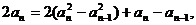
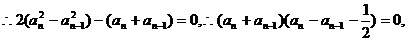
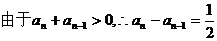 ,所以{an}是以a1=1,公差为
,所以{an}是以a1=1,公差为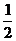 的等差数列,
的等差数列,
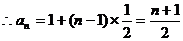 .………………………………10分
.………………………………10分
(Ⅲ)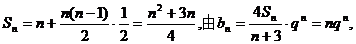

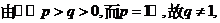
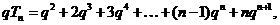
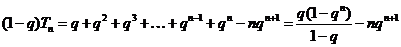
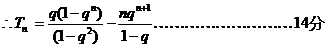
20. (1)证明:设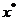 为
为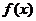 的峰点,则由单峰函数定义可知,
的峰点,则由单峰函数定义可知, 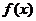 在
在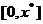 上单调递增, 在
上单调递增, 在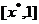 上单调递减,
上单调递减,
当 时,假设
时,假设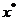
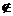
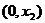 ,则
,则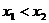 <
<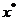 ,从而
,从而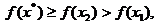 这与
这与 矛盾,所以
矛盾,所以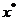
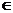
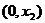 ,即
,即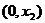 为含峰区间.
为含峰区间.
当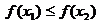 时,假设
时,假设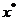
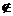
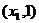 ,则
,则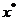
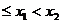 ,从而
,从而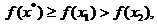 这与
这与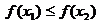 矛盾,所以
矛盾,所以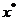
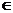
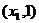 ,即
,即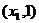 为含峰区间………………………….(7分)
为含峰区间………………………….(7分)
(2)证明:由(1)的结论可知:
当 时, 含峰区间的长度为
时, 含峰区间的长度为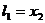 ;
;
当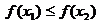 时, 含峰区间的长度为
时, 含峰区间的长度为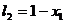 ;
;
对于上述两种情况,由题意得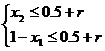 ①
①
由①得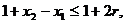 即
即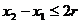 ,
,
又因为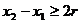 ,所以
,所以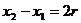 ②
②
将②代入①得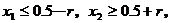 ③
③
由①和③解得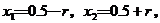
所以这时含峰区间的长度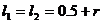 ,
,
即存在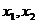 使得所确定的含峰区间的长度不大于
使得所确定的含峰区间的长度不大于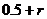 ………………………………(14分)
………………………………(14分)