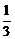网址:http://www.1010jiajiao.com/paper/timu/5155290.html[举报]
17、(本小题满分14分)如图,四棱锥P-ABCD中,PA⊥平面ABCD,PB与底面所成的角为45°,底面ABCD为直角梯形,∠ABC = ∠BAD = 90°,PA = BC = AD.
(Ⅰ)求证:平面PAC⊥平面PCD;
 (Ⅱ)在棱PD上是否存在一点E,使CE∥平面PAB ?若存在,请确定E点的位置;若不存在,请说明理由.
(Ⅱ)在棱PD上是否存在一点E,使CE∥平面PAB ?若存在,请确定E点的位置;若不存在,请说明理由.
数学(文)试题答案
一.选择题答案:1-5 ADCCA 6-10 BDBCB
二. 填空题: 本大题共4小题,每小题5分,共20分. 把正确答案填在题中横线上.
(11)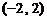 (12)
(12)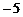 (13)
(13)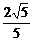 (14)②③ (15)
(14)②③ (15) (16)1
(16)1
16.
(I)证明: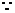
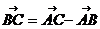 , ……………………………..(2分)
, ……………………………..(2分)
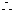
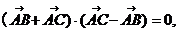
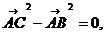 ………………………………(4分)
………………………………(4分)
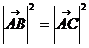 故
故 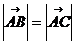 ……………(6分)
……………(6分)
(2)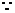
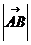 =2,
=2,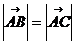 ,
, 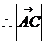 =2
又
=2
又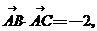
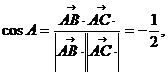 ………………………………….(10分)
………………………………….(10分)
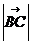 =
=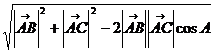 =
=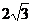 …………..(12分)
…………..(12分)
17、解:设PA = 1.
(Ⅰ)由题意 PA = BC = 1, AD = 2. …………………………………… 2分
∵ PA⊥面ABCD,∴ PB与面ABCD所成的角为∠PBA = 45°.
∴ AB = 1,由∠ABC = ∠BAD = 90°,易得CD = AC = .
由勾股定理逆定理得 AC⊥CD. …………………………………… 3分
又∵ PA⊥CD, PA∩AC = A,∴ CD⊥面PAC, …………………………………… 5分
又CD Ì 面PCD,
∴ 面PAC⊥面PCD. …………………………………… 6分
(Ⅱ)分别以AB, AD, AP所在直线分别为x轴, y轴, z轴建立空间直角坐标系.
∴ P(0, 0, 1), C(1, 1, 0), D(0, 2, 0). …………………………………… 8分
 |
设E(0, y, z),则= (0, y, z-1), = (0, 2, -1). …………………………………… 9分
∵ ∥,∴ y.(-1)-2 (z-1) = 0 … ① …………………………………… 10分
= (0, 2, 0) 是平面PAB的法向量, …………………………………… 11分
又 = (-1, y-1, z),由CE∥面PAB,∴ ⊥. …………………………… 12分
∴ (-1, y-1, z).(0, 1, 0) = 0,∴ y = 1,代入得z = . …………………………………13分
∴ E是PD中点,∴ 存在E点使得CE∥面PAB. …………………………………… 14分
18.解:设此工厂应分别生产甲、乙两种产品x吨y吨,获得利润z万元…………1分
|
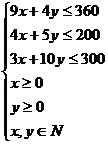 …………………………5分
…………………………5分
(图2分)
利润目标函数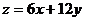 ………………………………8分
………………………………8分
如图,作出可行域,作直线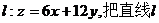 向右上方平移至l1位置,直线经过可行域上的点M,且与原点距离最大,此时
向右上方平移至l1位置,直线经过可行域上的点M,且与原点距离最大,此时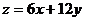 取最大值。……10分
取最大值。……10分
解方程组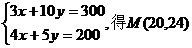 ………………………………12分
………………………………12分
所以生产甲种产品20t,乙种产品24t,才能使此工厂获得最大利润。……14分
19.解:(Ⅰ)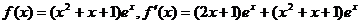
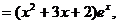 ………………………………………………………………3分
………………………………………………………………3分
当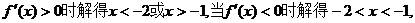
所以函数的单调增区间为(-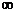 ,-3),(-1,+
,-3),(-1,+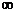 );
);
单调减区产为(-3,-1)………………………………6分)
(Ⅱ)
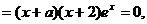 ……………………8分
……………………8分
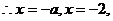
列表如下: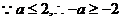 ……………………………………加表格12分
……………………………………加表格12分
|
x |
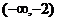 |
-2 |
(-2,-a) |
-a |
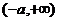 |
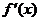 |
+ |
0 |
- |
0 |
+ |
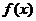 |
 |
极大 |
 |
极小 |
 |
由表可知 解得
解得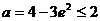 ,所以存在实数a,使
,所以存在实数a,使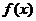 的极大值为3。………………………………………………14分
的极大值为3。………………………………………………14分
20.解答:(1)设动点P(x,y),
则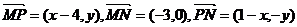 …………………………2分
…………………………2分
由已知得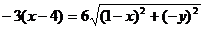 ,化简得
,化简得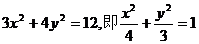
∴点P的轨迹是椭圆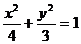 ……………………………………6分
……………………………………6分
(Ⅱ)设过N的直线l的方程为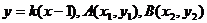
由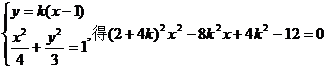 …………………………8分
…………………………8分
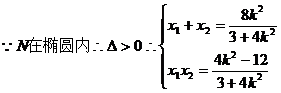 …………………………10分
…………………………10分
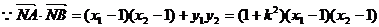
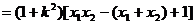
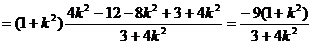 ……………………12分
……………………12分
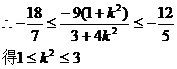
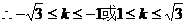 …………………………………………14分
…………………………………………14分
21.(Ⅰ)略;(Ⅱ)9;(Ⅲ)