
网址:http://www.1010jiajiao.com/paper/timu/5155349.html[举报]
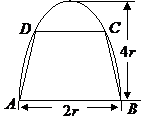 [例8]
(07年北京) 如图,有一块半椭圆形钢板,其半轴长
[例8]
(07年北京) 如图,有一块半椭圆形钢板,其半轴长
为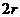 ,短半轴长为
,短半轴长为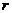 ,计划将此钢板切割成等腰梯形的形状,下
,计划将此钢板切割成等腰梯形的形状,下
底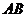 是半椭圆的短轴,上底
是半椭圆的短轴,上底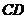 的端点在椭圆上,记
的端点在椭圆上,记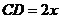 ,梯形面积为
,梯形面积为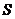 .
.
(I)求面积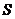 以
以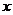 为自变量的函数式,并写出其定义域;
为自变量的函数式,并写出其定义域;
(II)求面积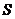 的最大值.
的最大值.
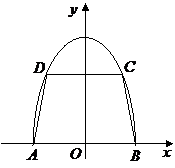 [解答](I)依题意,以
[解答](I)依题意,以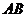 的中点
的中点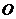 为原点建立直角坐标系
为原点建立直角坐标系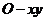 (如图),则点
(如图),则点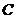 的横坐标为
的横坐标为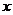 .点
.点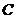 的纵坐标
的纵坐标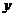 满足方程
满足方程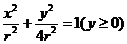 ,
,
解得,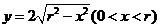 ,
,
所以,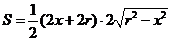
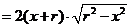 ,定义域为
,定义域为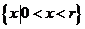 .
.
(II)记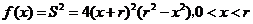 ,
,
则,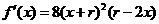 .
.
令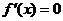 ,得
,得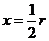 .
.
因为当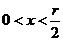 时,
时,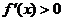 ;当
;当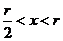 时,
时, ,
,
所以
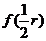 是
是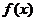 的最大值.
的最大值.
因此,当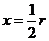 时,
时,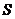 也取得最大值,最大值为
也取得最大值,最大值为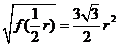 .
.
即梯形面积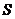 的最大值为
的最大值为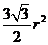 .
.
[说明] 该题以椭圆为载体,以函数思想为灵魂,以不等式、导数、三角函数等为工具,非常自然地将解析几何与导数、函数、方程、不等式、三角函数等重要数学基础知识有机交汇融为一体,无矫揉造作之嫌,是近年来较为成功的试题之一.
[例9] (07年上海) 已知函数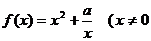 ,常数
,常数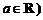 .
.
(1)讨论函数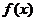 的奇偶性,并说明理由;
的奇偶性,并说明理由;
(2)若函数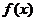 在
在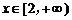 上为增函数,求
上为增函数,求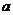 的取值范围.
的取值范围.
[解答] (1)当 时,
时, ,
,
对任意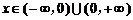 ,
,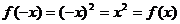 ,
,
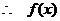 为偶函数.
为偶函数.
当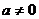 时,
时,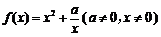 ,
,
取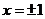 ,得
,得
 ,
,
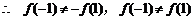 ,
,
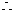 函数
函数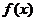 既不是奇函数,也不是偶函数.
既不是奇函数,也不是偶函数.
(2)解法一:设 ,
,
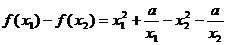
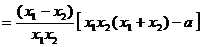 ,
,
要使函数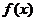 在
在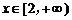 上为增函数,必须
上为增函数,必须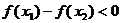 恒成立.
恒成立.
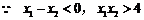 ,即
,即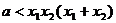 恒成立.
恒成立.
又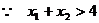 ,
,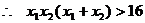 .
.
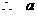 的取值范围是
的取值范围是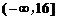 .
.
解法二:当 时,
时, ,显然在
,显然在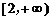 为增函数.
为增函数.
当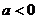 时,反比例函数
时,反比例函数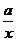 在
在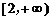 为增函数,
为增函数,
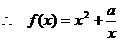 在
在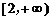 为增函数.
为增函数.
当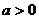 时,同解法一.
时,同解法一.
[说明] 本题考查了函数的性质问题,尤其是单调性的定义法证明更要引起注意.