
网址:http://www.1010jiajiao.com/paper/timu/5155404.html[举报]
12.已知函数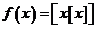 (
(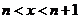 ),其中[x]表示不超过x的最大整数,如[-2.1]=-3,[-3]=-3,[2.5]=2.定义
),其中[x]表示不超过x的最大整数,如[-2.1]=-3,[-3]=-3,[2.5]=2.定义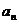 是函数
是函数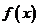 的值域中的元素个数,数列
的值域中的元素个数,数列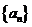 的前n项和为
的前n项和为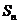 ,则满足
,则满足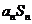
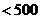 的最大正整数n= .
的最大正整数n= .
选做题:
数学试题(理科4)参考答案
1-8: C B A B A C A B
9. 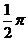 ;
10.
;
10. 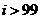 ,
,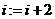 ; 11.
; 11. 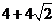 ; 12. 9; 13. 9; 14.
; 12. 9; 13. 9; 14. 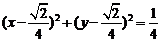 ; 15.
; 15. 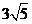
16.解:(1)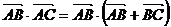
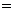
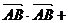
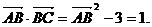
∴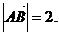 即AB边的长度为2.
…………… …………5分
即AB边的长度为2.
…………… …………5分
(2)由已知及(1)有: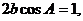
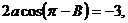
∴ ……………8分
……………8分
由正弦定理得: 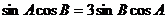 ……………10分
……………10分
∴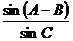 =
=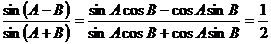 …………12分
…………12分
17.解:⑴智力正常的人将这5道试题都答错了的概率
为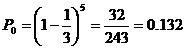 ……………3分
……………3分
答对了的4道试题的概率为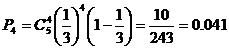
答对了的5道试题的概率为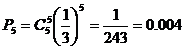
∴智力正常的人答对了的4道试题以上的概率为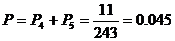 …7分
…7分
⑵智力正常的人将这5道试题都答错了的概率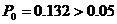 因而不能判定甲的智力低于正常水平
……9分
因而不能判定甲的智力低于正常水平
……9分
 智力正常的人答对了的4道试题以上的概率
智力正常的人答对了的4道试题以上的概率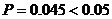 .根据小概率事件在一次试验中几乎不发生的原理知,假设乙的智力在正常水平, 答对了的4道试题的情况几乎不发生.从而可以认定乙的智力高于正常水平。
…………12分
.根据小概率事件在一次试验中几乎不发生的原理知,假设乙的智力在正常水平, 答对了的4道试题的情况几乎不发生.从而可以认定乙的智力高于正常水平。
…………12分
18.解法一:
(1)在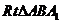 中,
中,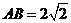 ,
,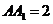 ,
,
∴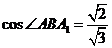 ,取
,取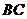 中点
中点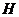 ,
,
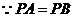 ,
, 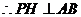 ,
,
在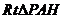 中,
中,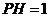 ,
,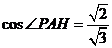 ,又
,又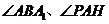 均为锐角,∴
均为锐角,∴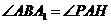 , ---------------2分
, ---------------2分
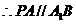 ,又
,又 外,
外, 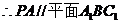 .
---------------4分
.
---------------4分
(2)∵平面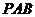
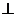 平面
平面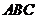 ,∴
,∴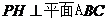 ,过
,过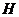 作
作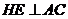 于
于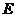 ,连结
,连结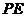 ,
,
则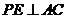 ,
,
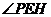 为二面角
为二面角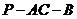 的平面角, ------------------------6分
的平面角, ------------------------6分
易知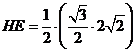 =
=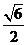 ,∴
,∴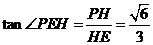 , ------------------------9分
, ------------------------9分
(3)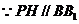 ,
, 点到平面
点到平面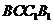 的距离,就是
的距离,就是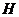 到平面
到平面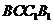 的距离, --------11分
的距离, --------11分
过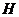 作
作 于
于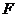 ,则
,则 ,
,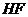 的长度即为所求,
由上
的长度即为所求,
由上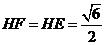 (或用等体积
(或用等体积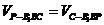 求)----------------------------------14分
求)----------------------------------14分
解法二:建立图示空间直角坐标系.
则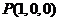 ,
,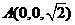 ,
,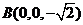 ,
,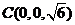 ,
,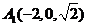 .
.
(1)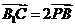
(2)利用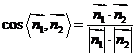 ,其中
,其中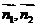 分别为两个半平面的法向量..
分别为两个半平面的法向量..
(3)利用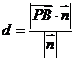 ,其中
,其中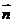 为平面
为平面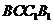 的法向量。
的法向量。
19. (Ⅰ)证明: 
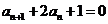 ………... 3分
………... 3分
(Ⅱ)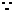
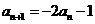 ∴
∴ 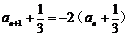 ……………………….………..5分
……………………….………..5分
又
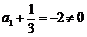 ∴
∴ 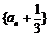 为等比数列………………………………………….6分
为等比数列………………………………………….6分
∴ 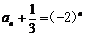 ∴
∴ 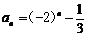 ……………………………………………………8分
……………………………………………………8分
(Ⅲ)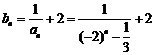 ∴
∴ 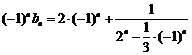 …………………. 10分
…………………. 10分
当n为偶数时,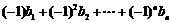
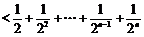
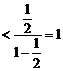 …14分
…14分
20. 解:(1)设点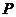
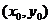 ,则
,则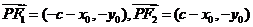 ,
,
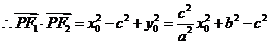 ,
,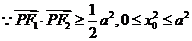
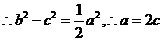 ,又
,又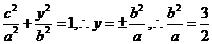 ,
,
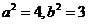 ,∴椭圆的方程为:
,∴椭圆的方程为: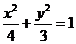
(2)当过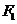 直线
直线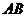 的斜率不存在时,点
的斜率不存在时,点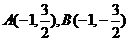 ,则
,则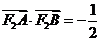 ;
;
当过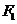 直线
直线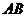 的斜率存在时,设斜率为
的斜率存在时,设斜率为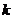 ,则直线
,则直线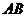 的方程为
的方程为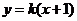 ,
,
设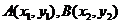 , 由
, 由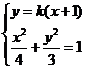 得:
得: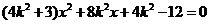
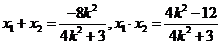
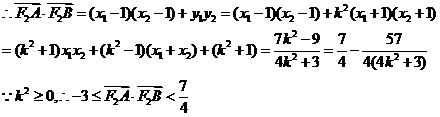
综合以上情形,得: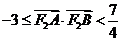
21. 解:(Ⅰ)当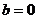 时,
时,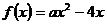 ,
,
若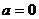 ,
,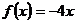 ,则
,则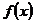 在
在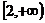 上单调递减,不符题意.
上单调递减,不符题意.
故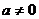 ,要使
,要使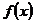 在
在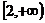 上单调递增,必须满足
上单调递增,必须满足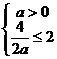 ,∴
,∴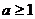 .
.
(Ⅱ)若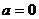 ,
,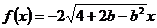 ,则
,则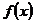 无最大值,故
无最大值,故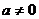 ,∴
,∴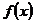 为二次函数.
为二次函数.
要使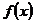 有最大值,必须满足
有最大值,必须满足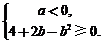 即
即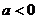 ,且
,且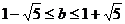 .
.
此时,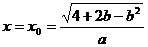 时,
时,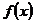 有最大值.
有最大值.
又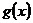 取最小值时,
取最小值时,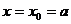 ,依题意,有
,依题意,有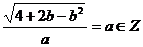 ,
,
则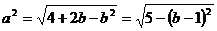 .
.
∵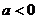 ,且
,且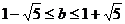 ,∴
,∴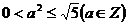 ,得
,得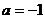 ,此时
,此时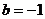 或
或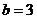 .
.
∴满足条件的实数对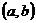 是
是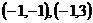 .
.
(Ⅲ)当实数对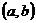 是
是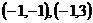 时,
时,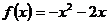 .
.
依题意,只需构造以2(或2的正整数倍)为周期的周期函数即可.
如对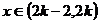 ,
,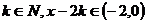 ,
,
此时,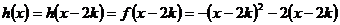 ,
,
故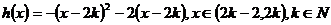 .
.