
网址:http://www.1010jiajiao.com/paper/timu/5155432.html[举报]
19.(本小题满分16分)设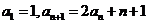 。
。
(1)是否存在常数p,q,使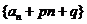 为等比数列?若存在,求出p,q的值。若不存在,说明理由;
为等比数列?若存在,求出p,q的值。若不存在,说明理由;
(2)求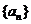 的通项公式;
的通项公式;
(3)当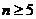 时,证明:
时,证明: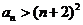 。
。
数 学试题(3理科) 参考答案
一、选择题:本大题共8小题,每小题5分,共40分。
1.D 2.A 3.C 4.D 5.C 6.B 7.B 8. D
二、填空题:本大题共6小题,每小题5分,共30分
9. 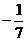 10.
10.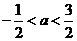 11.1 12.
11.1 12.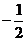 13.
13.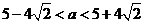 14.(1) 射线 (2)
14.(1) 射线 (2)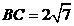 (3) 6
(3) 6
三、解答题:本大题共5小题,共70分,解答应写出文字说明,证明过程或演算步骤。
15. ∵ 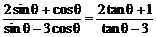
∴ 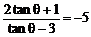
∴ tanθ=2
∴ 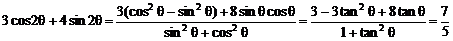
16.(本小题满分12分)
解:对任一人,其血型为A,B,AB,O型血的事件分别记为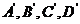 ,它们是互斥的。由已知有:
,它们是互斥的。由已知有:
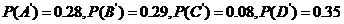 ,因为B,O型血可以输给B型血的人,故“可以输给B型血的人”为事件
,因为B,O型血可以输给B型血的人,故“可以输给B型血的人”为事件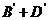 ,根据互斥事件的加法公式有:
,根据互斥事件的加法公式有:
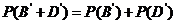 =0.29+0.35=0.64
=0.29+0.35=0.64
(2)由于A,AB型血不能输给B型血的人,故“不能输给B型血的人”为事件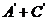 ,
,
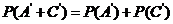 =0.28+0.08=0.36
=0.28+0.08=0.36
答:任找一人,其血可以输给小明的概率是0.64,任找一人,其血不能输给小明的概率是0.36
17.(本小题满分12分)
解:(1)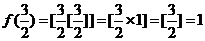
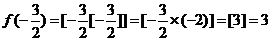
(2)由(1)知: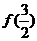
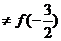 ,且
,且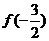
 ,
,
故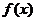 为非奇非偶函数。
为非奇非偶函数。
(3)当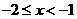 时,
时,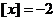 ,则
,则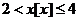 , 所以
, 所以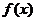 可取2,3,4。
可取2,3,4。
当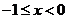 时,
时,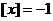 ,则
,则 , 所以
, 所以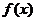 可取0,1。
可取0,1。
当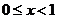 时,
时,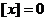 ,则
,则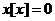 , 所以
, 所以 。
。
当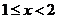 时,
时,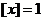 ,则
,则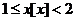 , 所以
, 所以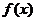 =1。
=1。
当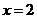 时,
时,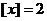 ,则
,则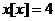 , 所以
, 所以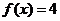 。
。
所以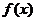 的值域为{0,1,2,3,4}.
的值域为{0,1,2,3,4}.
|
|
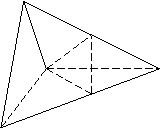
解:(1)取AC中点P,由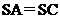 知:
知: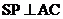

|

|
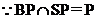
|
|
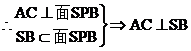
(2)由(1)知: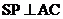 ,又平面
,又平面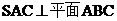 ,
,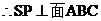
 取BP中点Q,连结NQ
取BP中点Q,连结NQ
又N为SB中点
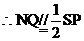 ,而
,而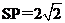 ,
,
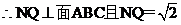
过Q作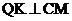 ,连结NK,
,连结NK,
则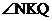 即为二面角N-CM-B的平面角
即为二面角N-CM-B的平面角
设CM交BP于O,则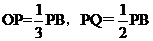 ,
,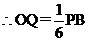
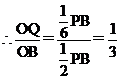
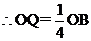
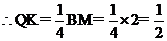

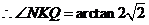
所以二面角N-CM-B的大小为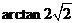 。
。
(3)由(2)知: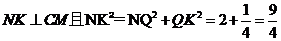
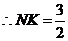
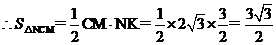
设B到平面CMN的距离为d,则
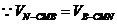 ,
, 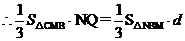
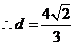
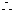 点B到平面CMN的距离为
点B到平面CMN的距离为 。
。
19.(本小题满分16分)
解:(1)由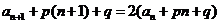 得:
得:
可见:应有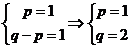
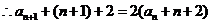
因此存在常数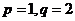 使
使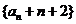 为等比数列。
为等比数列。
(2)由于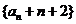 是以
是以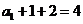 为首项2为公比的等比数列
为首项2为公比的等比数列
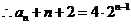
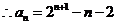
(3)当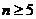 时,
时,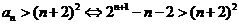
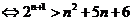 。
。
而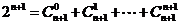
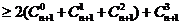
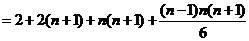 (
(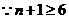 )
)
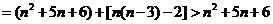
 当
当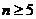 时,
时,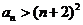 。
。
 20.(本小题满分15分)
20.(本小题满分15分)
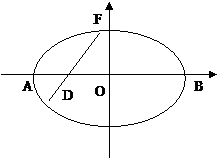
解:(1)如图,建立平面直角坐标系,则D(-1,0)
弦EF所在的直线方程为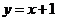
设椭圆方程为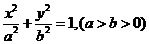
设 ,由
,由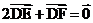 知:
知: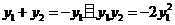
联立方程组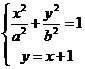 ,消去x得:
,消去x得: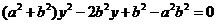
由题意知: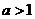 ,
,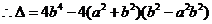
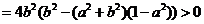
由韦达定理知: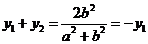
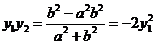
消去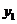 得:
得: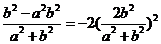 ,化简整理得:
,化简整理得: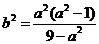
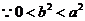
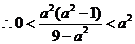 解得:
解得: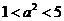
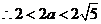
即:椭圆的长轴长的取值范围为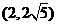 。
。
(2)若D为椭圆的焦点,则c=1,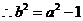
由(1)知: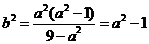
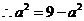
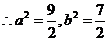
 椭圆方程为:
椭圆方程为: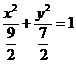 。
。