
网址:http://www.1010jiajiao.com/paper/timu/5155436.html[举报]
3. 一个与球心距离为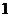 的平面截球所得圆的面积为
的平面截球所得圆的面积为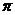 ,则球的表面积为 (
B )
,则球的表面积为 (
B )
A. B.
B.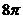 C.
C.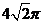 D.
D.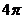
数 学 试 题 ( 理 科 2 )参考答案
一.选择题 A C B B A B B C
二.填空题 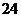 ;
;
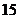 ;
;
 ; ③④;
; ③④; 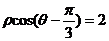 ;
; 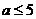 ;
; 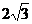 。
。
三.解答题
16.解:(Ⅰ)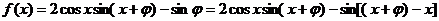
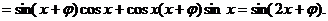 ……………2分
……………2分
由题意知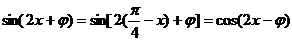 对任意实数x恒成立,
对任意实数x恒成立,
得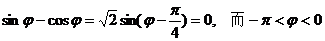 ,
,
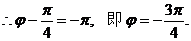 ………………………………………………………6分
………………………………………………………6分
(Ⅱ)由(Ⅰ)知
由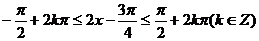 ,解得
,解得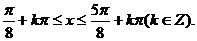
所以,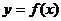 的单调增区间为
的单调增区间为 ……………………12分
……………………12分
17.解:(Ⅰ)密码中不同数字的个数为2的事件为密码中只有两个数字,注意到密码的第1,2列分别总是1,2,即只能取表格第1,2列中的数字作为密码.
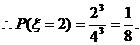 …………………………………………………………………4分
…………………………………………………………………4分
(Ⅱ)由题意可知,ξ的取值为2,3,4三种情形.
若ξ=
3,注意表格的第一排总含有数字1,第二排总含有数字2则密码中只可能取数字1,2,3或1,2,4.

若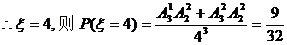
(或用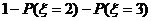 求得). ………………………………………………8分
求得). ………………………………………………8分
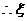 的分布列为:
的分布列为:
|
ξ |
2 |
3 |
4 |
|
p |
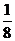 |
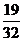 |
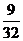 |
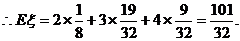 ………………………………………………12分
………………………………………………12分
18.证明:(1)当点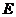 为
为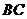 的中点时,
的中点时,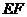 与平面
与平面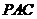 平行.
平行.
∵在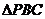 中,
中,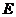 、
、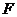 分别为
分别为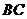 、
、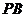 的中点
的中点
∴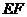 ∥
∥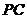 又
又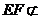 平面
平面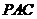 ,而
,而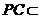 平面
平面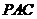
∴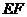 ∥平面
∥平面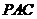 .
……………………4分
.
……………………4分
(2)证明(略证):易证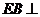 平面
平面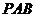 ,又
,又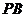 是
是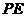 在平面
在平面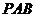 内的射影,
内的射影,
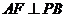 ,∴
,∴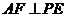 .
……………………8分
.
……………………8分
(3)∵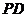 与平面
与平面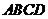 所成的角是
所成的角是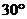 ,∴
,∴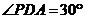 ,
,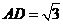 ,
,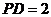 .
.
 过
过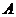 作
作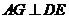 于
于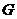 ,连
,连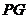 ,则
,则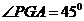 .
…………………10分
.
…………………10分
易知: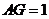 ,
,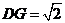 ,设
,设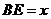 ,则
,则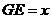 ,
,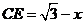 ,
,
在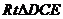 中,
中,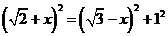 ,
,
得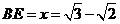 .
………14分
.
………14分
解法二:(向量法)(1)同解法一
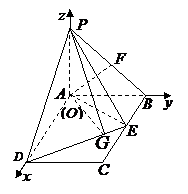 (2)建立图示空间直角坐标系,则
(2)建立图示空间直角坐标系,则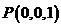 ,
,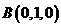 ,
,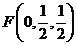 ,
,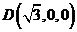 .
.
设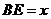 ,则
,则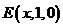 ,
,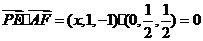
∴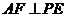 (本小题4分)
(本小题4分)
(3)设平面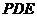 的法向量为
的法向量为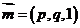 ,由
,由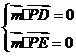 ,
,
得: ,依题意
,依题意 ,
,
∴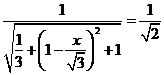 ,得
,得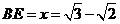 .
(本小题6分)
.
(本小题6分)
19.解:依题意有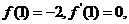 而
而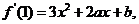

故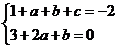 得
得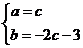 从而
从而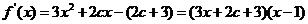 。
。
令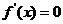 ,得
,得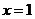 或
或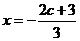 。
。
由于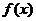 在
在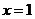 处取得极值,故
处取得极值,故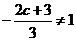 ,即
,即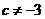 。
。
(1) 若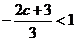 ,即
,即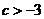 ,则当
,则当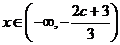 时,
时,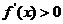 ;
;
当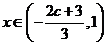 时,
时,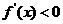 ;当
;当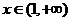 时,
时,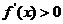 ;
;
从而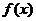 的单调增区间为
的单调增区间为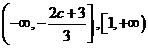 ;单调减区间为
;单调减区间为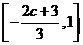
(2) 若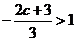 ,即
,即 ,同上可得,
,同上可得,
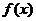 的单调增区间为
的单调增区间为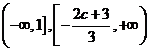 ;单调减区间为
;单调减区间为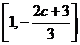
20.解:(Ⅰ)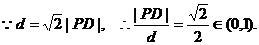
∴点P的轨迹是D为焦点,l为相应准线的椭圆.
由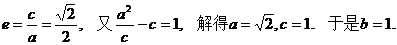
以CD所在直线为x轴,以CD与⊙D的另一个交点O为坐标原点建立直角坐标系.
∴所求点P的轨迹方程为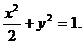 ………………………………………………6分
………………………………………………6分
(说明:其它建系方式相应给分)
(Ⅱ)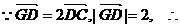 G为椭圆的左焦点.
G为椭圆的左焦点.
又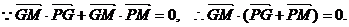
由题意,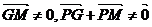 (否则P、G、M、D四点共线与已经矛盾)
(否则P、G、M、D四点共线与已经矛盾)
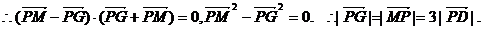
又∵点P在椭圆上, 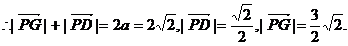
又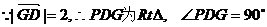
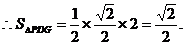 ……………………………………………………14分
……………………………………………………14分
21.解:(Ⅰ)令 ,
,
则无穷数列{an}可由a1 = 1,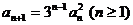 给出.
给出.
显然,该数列满足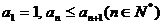 ,且
,且
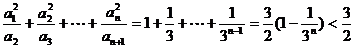 ……………………6分
……………………6分
(Ⅱ)
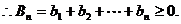 ………………………………………………8分
………………………………………………8分
又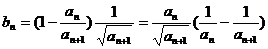
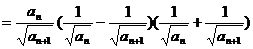

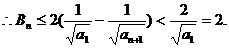
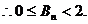 …………………………………………………………………14分
…………………………………………………………………14分