
网址:http://www.1010jiajiao.com/paper/timu/5155463.html[举报]
9. 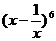 的展开式中的常数项是
(用数字作答).
的展开式中的常数项是
(用数字作答).
数学试题参考答案和评分标准(理科1)
一、选择题(每题5分,共40分)
|
序号 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
|
答案 |
A |
B |
D |
B |
C |
A |
D |
C |
二、填空题(每题5分,共30分)
9.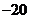 .
10.3m与1.5m. 11.
.
10.3m与1.5m. 11.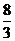 .
.
12.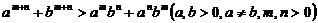 (或
(或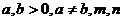 为正整数).注:填
为正整数).注:填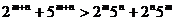 以及是否注明字母的取值符号和关系,均不扣分;
以及是否注明字母的取值符号和关系,均不扣分;
若填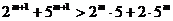 或
或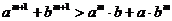 可给3分.
可给3分.
13.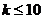 . 14.<.
. 14.<.
三、解答题(本大题共6小题,共80分)
15. 解:(1) 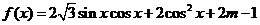 ……………………………………………………2分
……………………………………………………2分
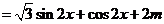 ………………………………………………………………………………………………4分
………………………………………………………………………………………………4分
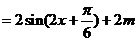 . …………………………………………………………………………………………………………6分
. …………………………………………………………………………………………………………6分
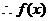 的最小正周期是
的最小正周期是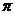 . …………………………………………………………………………………………………7分
. …………………………………………………………………………………………………7分
(2) ∵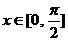 ,∴
,∴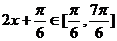 …………………………………………………………………8分
…………………………………………………………………8分
∴当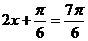 即
即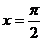 时,函数
时,函数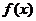 取得最小值是
取得最小值是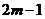 . ………………………10分
. ………………………10分
∵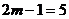 ,∴
,∴ . …………………………………………………………………………………………………12分
. …………………………………………………………………………………………………12分
16. 方法一:(2) 证明:当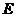 为
为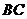 中点时,
中点时, ,从而
,从而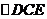 为等腰直角三角形,则
为等腰直角三角形,则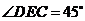 ,同理可得
,同理可得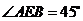 ,∴
,∴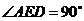 ,于是
,于是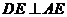 ,…2分
,…2分
又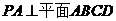 ,且
,且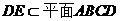 ,∴
,∴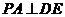 ,…………………………………………4分
,…………………………………………4分
∴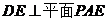 ,又
,又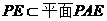 ,∴
,∴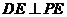 . …………………………………………………6分
. …………………………………………………6分
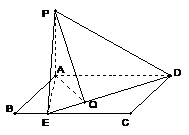 (也可以利用三垂线定理证明,但必需指明三垂线定理)
(也可以利用三垂线定理证明,但必需指明三垂线定理)
(2) 如图过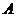 作
作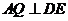 于
于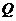 ,连
,连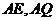 ,则
,则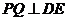 ,
,
∴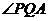 为二面角
为二面角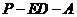 的平面角. ………8分
的平面角. ………8分
设 ,则
,则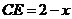 .
.
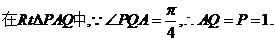
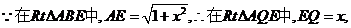
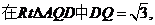 于是
于是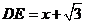 …………………………………………………………10分
…………………………………………………………10分
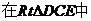 ,有
,有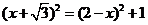
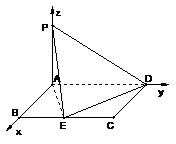 解之得
解之得 。
。
点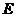 在线段BC上距B点的
在线段BC上距B点的 处. …………………………………………………………………………12分
处. …………………………………………………………………………12分
方法二、向量方法.以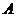 为原点,
为原点,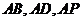 所在直线为
所在直线为
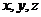 轴,建立空间直角坐标系,如图. …………………………1分
轴,建立空间直角坐标系,如图. …………………………1分
(1)不妨设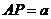 ,则
,则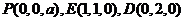 ,
,
从而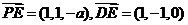 ,………………………4分
,………………………4分
于是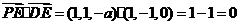 ,
,
所以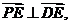 所以
所以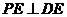 …………………………………………………………………………………6分
…………………………………………………………………………………6分
(2)设 ,则
,则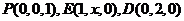 ,
,
则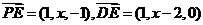 .………………………………………………………………………………8分
.………………………………………………………………………………8分
易知向量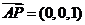 为平面
为平面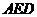 的一个法向量.设平面
的一个法向量.设平面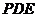 的法向量为
的法向量为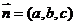 ,则应有
,则应有
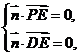 即
即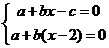 解之得
解之得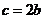 ,令
,令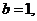 则
则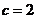 ,
,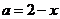 ,
,
从而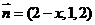 ,………………………………………………………………………………………………………10分
,………………………………………………………………………………………………………10分
依题意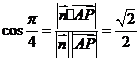 ,即
,即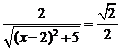 ,解之得
,解之得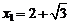 (舍去),
(舍去),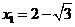
所以点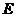 在线段BC上距B点的
在线段BC上距B点的 处.…………………………………………………………………12分
处.…………………………………………………………………12分
17. 解:(1)由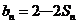 ,令
,令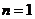 ,则
,则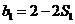 ,又
,又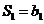 ,所以
,所以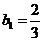 .
.
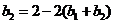 ,则
,则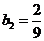 . ……………………………………………………………………………………2分
. ……………………………………………………………………………………2分
当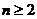 时,由
时,由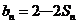 ,可得
,可得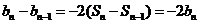 .
.
即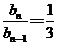 . …………………………………………………………………………………………………………………………4分
. …………………………………………………………………………………………………………………………4分
所以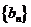 是以
是以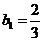 为首项,
为首项,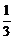 为公比的等比数列,于是
为公比的等比数列,于是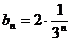 . …………5分
. …………5分
(2)数列 为等差数列,公差
为等差数列,公差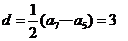 ,可得
,可得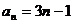 . ………………7分
. ………………7分
从而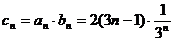 .
……………………………………………………………………………………8分
.
……………………………………………………………………………………8分
∴ ……………10分
……………10分
∴ .
…………………11分
.
…………………11分
从而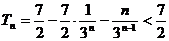 .
…………………………………………………………………………14分
.
…………………………………………………………………………14分
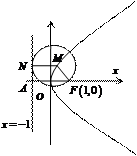 18.(1)如图,设
18.(1)如图,设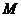 为动圆圆心,
为动圆圆心, 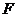
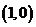 ,过点
,过点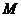 作直线
作直线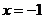 的垂线,垂足为
的垂线,垂足为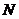 ,由题意知:
,由题意知: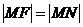 , ………………………………………………2分
, ………………………………………………2分
即动点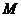 到定点
到定点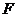 与定直线
与定直线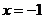 的距离相等,由抛物线的定义知,点
的距离相等,由抛物线的定义知,点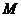 的轨迹为抛物线,其中
的轨迹为抛物线,其中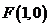 为焦点,
为焦点,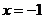 为准线, ∴ 动点
为准线, ∴ 动点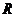 的轨迹方程为
的轨迹方程为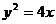 ………………………5分
………………………5分
(2)由题可设直线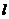 的方程为
的方程为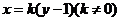 ,
,
由 得
得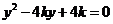
△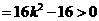 ,
,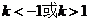 ………………………………………………………………………………7分
………………………………………………………………………………7分
设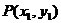 ,
,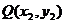 ,则
,则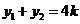 ,
,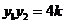 ……………………………………………9分
……………………………………………9分
由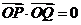 ,即
,即 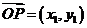 ,
,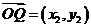 ,于是
,于是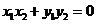 ,……11分
,……11分
即 ,
,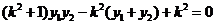 ,
,
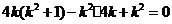 ,解得
,解得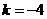 或
或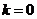 (舍去),…………………………………13分
(舍去),…………………………………13分
又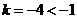 , ∴ 直线
, ∴ 直线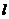 存在,其方程为
存在,其方程为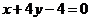 ………………………………………14分
………………………………………14分
19. 解:(1)这8位同学中恰有3位同学的数学和物理分数均为优秀,则需要先从物理的4个优秀分数中选出3个与数学优秀分数对应,种数是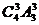 (或
(或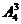 ),然后将剩下的5个数学分数和物理分数任意对应,种数是
),然后将剩下的5个数学分数和物理分数任意对应,种数是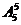 。根据乘法原理,满足条件的种数是
。根据乘法原理,满足条件的种数是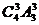
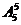 。 …………………………………………………………………………………………………………………………………4分
。 …………………………………………………………………………………………………………………………………4分
这8位同学的物理分数和数学分数分别对应的种数共有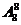 。 ………………………………5分
。 ………………………………5分
故所求的概率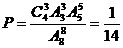 . ………………………………………………………………………………6分
. ………………………………………………………………………………6分
(2) 变量y与x、z与x的相关系数分别是
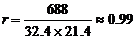 、
、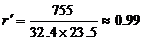 .
.
可以看出,物理与数学、化学与数学的成绩都是高度正相关. …………………………8分
(3) 设y与x、z与x的线性回归方程分别是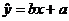 、
、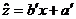 .
.
根据所给的数据,可以计算出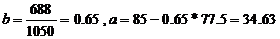 ,
,
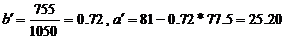 . ……………………………………………………10分
. ……………………………………………………10分
所以y与x和z与x的回归方程分别是
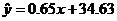 、
、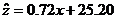 . …………………………………………………………11分
. …………………………………………………………11分
又y与x、z与x的相关指数是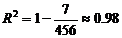 、
、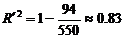 . ……13分
. ……13分
故回归模型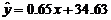 比回归模型
比回归模型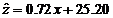 的拟合的效果好. …14分
的拟合的效果好. …14分
20. (Ⅰ)由 ,得
,得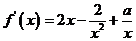 ……………………………………2分
……………………………………2分
函数为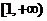 上单调函数. 若函数为
上单调函数. 若函数为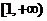 上单调增函数,则
上单调增函数,则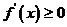 在
在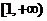 上恒成立,即不等式
上恒成立,即不等式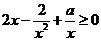 在
在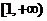 上恒成立. 也即
上恒成立. 也即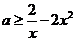 在
在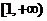 上恒成立. ……………………………………………………………………………………………………………………………………………4分
上恒成立. ……………………………………………………………………………………………………………………………………………4分
令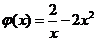 ,上述问题等价于
,上述问题等价于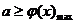 ,而
,而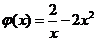 为在
为在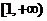 上的减函数,则
上的减函数,则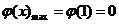 ,于是
,于是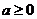 为所求. …………………………………………………………6分
为所求. …………………………………………………………6分
(Ⅱ)证明:由 得
得
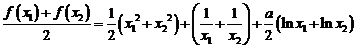
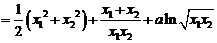 ……………………………………………………………………………7分
……………………………………………………………………………7分
 ………………………………………………………………8分
………………………………………………………………8分
而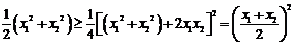 ① ………………………………………10分
① ………………………………………10分
又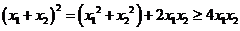 , ∴
, ∴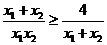 ② …………11分
② …………11分
∵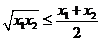 ∴
∴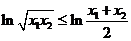 ,
,
∵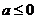 ∴
∴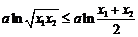 ③ ……………………………………………………………………13分
③ ……………………………………………………………………13分
由①、②、③得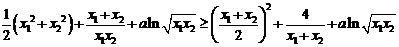
即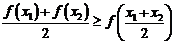 ,从而由凹函数的定义可知函数为凹函数. …………14分
,从而由凹函数的定义可知函数为凹函数. …………14分