
网址:http://www.1010jiajiao.com/paper/timu/5155486.html[举报]
12、如果直线y=kx+1与圆x2+y2+kx+my-4=0交于M、N两点,且M、N关于直线x-y=0对称,动点P(a,b)在不等式组:表示的平面区域内部及边界上运动,则ω=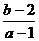 的取值范围是
(
)
的取值范围是
(
)
A、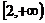 B、
B、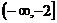 C、
C、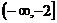 ∪
∪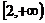 D、
D、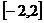
第Ⅱ卷(非选择题 共90分)
参考答案:
一、选择题:
|
题号 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
|
答案 |
A |
B |
C |
D |
D |
B |
D |
D |
C |
C |
A |
C |
简答与提示:
1、集合M是函数y=x+l的函数值的集合,集合N是圆上的点集.
2、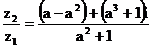 ,故a 3+1=0,得a =-1.
,故a 3+1=0,得a =-1.
3、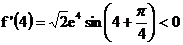 .
.
4、若使夹角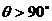 ,则有-m+n<0即m>n,其概率为
,则有-m+n<0即m>n,其概率为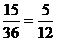 .
.
5、按定义计算
6、由已知f (3x+1)=f[3(x+3)+1]=f(3x+1+9),所以f(x)的周期为9,f(2006)=f(2007-1)=f(-1)=
-f(1)=1.
7、面积比是相似比的平方,体积比是相似比的立方
8、由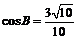 得
得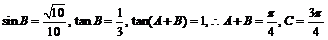 ,
,
∴∠C的对边AB为最长边,∠B的对边AC为最短边,由正弦定理得:
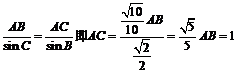
9、∵Sn有最小值,∴d<0则a10>a11,又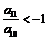 ,∴a11<0<a10 ∴a10+a11<0,
,∴a11<0<a10 ∴a10+a11<0,
S20=10(a1+a20)=10(a10+a11)<0, S19=19a10>0又a1>a2>…>a10>0>a11>a12>…
∴S10>S9>…>S2>S1>0, S10>S11>…>S19>0>S20>S21>…
又∵S19−S1=a2+a3+…+a19=9(a10+a11)<0 ∴S19为最小正值
10、由不等式x2+ax−3a<0, x∈[−1, 1]时恒成立,可得不等式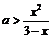 ,x∈[−1,
1]时恒成立,令
,x∈[−1,
1]时恒成立,令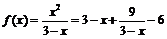 ,由x∈[−1,
1]得3−x∈[2, 4],当3−x=3即x=0时,函数f(x)有最小值0,又
,由x∈[−1,
1]得3−x∈[2, 4],当3−x=3即x=0时,函数f(x)有最小值0,又
11、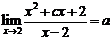
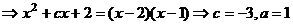 ,
,
∴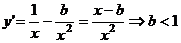 或
或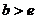
12、 M、N关于直线x-y=0对称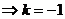 且圆心
且圆心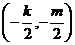 在直线x-y=0上,从而
在直线x-y=0上,从而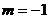
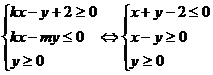 ;ω=
;ω=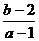 看成斜率。
看成斜率。
二、填空题:
13、 14、60o 15、0 16、①②③④
简答与提示:
13、直线对称
14、将正方体复原
15、0 两边求导,再分别把x赋值x=2,x=0,最后把所得两式相乘即得.
16、①注意到G≠0; ②cosαcosβ=1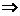 cosα=cosβ=1或cosα=cosβ=-1;
cosα=cosβ=1或cosα=cosβ=-1;
③ 记f(x)=|x-4|+|x-3|<a,依题意则有a≥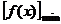 1;
1;
④ y=sinx+sin|x| 。
。
三、解答题:
17、(本小题满分12分)
解:设甲先答A、B所获奖金分别为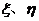 元,则有
元,则有
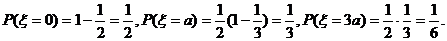 …… 3分
…… 3分
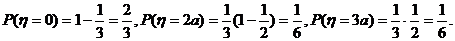 ……6分
……6分
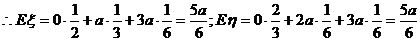 …………10分
…………10分
由于两种答序获奖金的期望相等,故先答哪个都一样。 …………………………12分
18、(本小题满分12分)
解:(Ⅰ)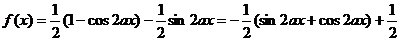
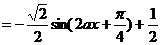 …………………………………4分
…………………………………4分
∵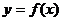 的图象与
的图象与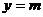 相切.
相切.
∴m为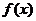 的最大值或最小值.
即
的最大值或最小值.
即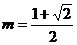 或
或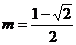 ……6分
……6分
(Ⅱ)又因为切点的横坐标依次成公差为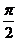 的等差数列.所以
的等差数列.所以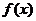 最小正周期为
最小正周期为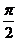 .
.
又
 所以
所以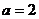 ……………………………8分
……………………………8分
即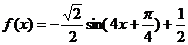 ……………………………………9分
……………………………………9分
令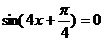 .则
.则
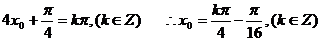 ………………………10分
………………………10分
由0≤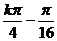 ≤
≤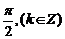 得k=1,2,
得k=1,2,
因此对称中心为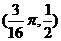 、
、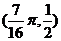 . ……………………………12分
. ……………………………12分
19、(本题满分12分)
解:⑴解法一:如图1,证明0M=0N=MN=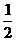 AB=
AB=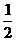 BC=
BC=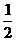 AC,从而∠MON=
AC,从而∠MON=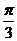
∴点E、F在该球面上的球面距离为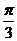 .
.
解法二:如图2,补形易证:∠EOF=∠GOH =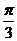 .
.
解法三:其实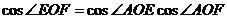 ,易证:∠EOF=
,易证:∠EOF=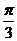 .
.
解法四:如图3,建立空间直角坐标系,易知E(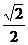 ,0,
,0, 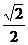 )、F(0,
)、F(0,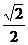 ,
, 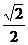 )
)
∴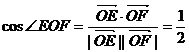 ,从而∠EOF =
,从而∠EOF =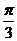 . …………………6分
. …………………6分
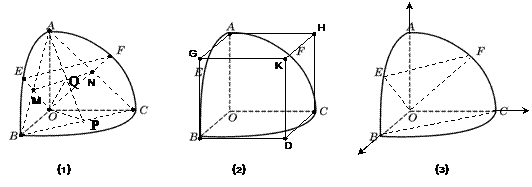 |
⑵ 解法一:如图1,取BC中点P,连接AP交MN与Q,则易证,∠POQ就是所求二面角的平面角。
在三角形OPQ中,OP=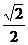 ,PQ=OQ=
,PQ=OQ=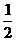 AP=
AP=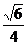 ,可解得cos∠POQ=
,可解得cos∠POQ=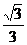 ,
,
∴∠POQ=arcos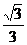 (=arctan
(=arctan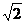 ).
……………………………12分
).
……………………………12分
解法二:如图2,补形成正方体去解决.
解法三:如图3,建立空间直角坐标系去求解。
20、(本题满分12分)
解:(Ⅰ)因为点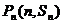 都在函数
都在函数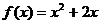 的图象上
的图象上
所以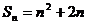
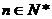
当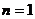 时,
时,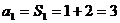 ……………………………………………2分
……………………………………………2分
当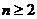 时,
时,
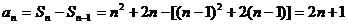 (*) ……………3分
(*) ……………3分
令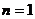 ,
,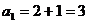 ,也满足(*)式
,也满足(*)式
所以,数列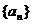 的通项公式是
的通项公式是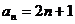 . …………………………………4分
. …………………………………4分
(Ⅱ)由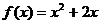 求导可得
求导可得
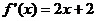
∵ 过点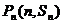 的切线的斜率为
的切线的斜率为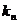
∴ 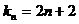 …………………………………………………………5分
…………………………………………………………5分
又∵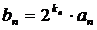
∴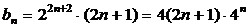 ……………………………6分
……………………………6分
∴ 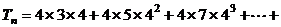
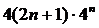 ① 由①
① 由①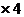 可得
可得
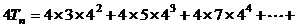
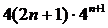 ②
②
①-②可得
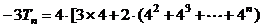
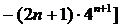
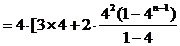
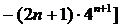
∴ 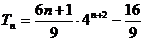 ……………………………………………………8分
……………………………………………………8分
(Ⅲ)∵ ,
,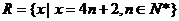
∴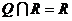 --------------------------- 10分
--------------------------- 10分
又∵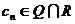 ,其中
,其中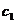 是
是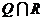 中的最小数,
中的最小数,
∴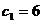 , --------------------------- 11分
, --------------------------- 11分
∴ 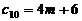
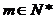 (
(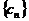 的公差是4 的倍数!)
的公差是4 的倍数!)
又∵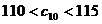
∴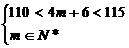 解得
解得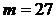
∴ ………………………………………………………………………10分
………………………………………………………………………10分
设等差数列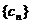 的公差为
的公差为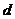
则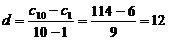
∴ 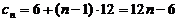
所以,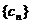 的通项公式为
的通项公式为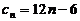 . ……………………………12分
. ……………………………12分
21、(本题满分12分)
(1)证明:由抛物线定义知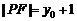 ,(2分)
,(2分)
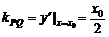 ,可得PQ所在直线方程为x0x=2(y+y0), ………………………4分
,可得PQ所在直线方程为x0x=2(y+y0), ………………………4分
得Q点坐标为(0, -y0),∴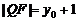 ,∴ |PF|=|QF|,∴△PFQ为等腰三角形。 …6分
,∴ |PF|=|QF|,∴△PFQ为等腰三角形。 …6分
(2)设A(x1, y1),B(x2, y2),又M点坐标为(0, y0), ∴AB方程为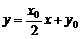 ,
,
由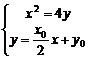 得
得
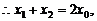
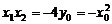 ……①
……①
由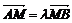 得:
得: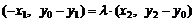 , ∴
, ∴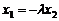 ……②
……②
由①②知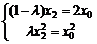 ,得
,得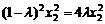 ,由x0≠0可得x2≠0,
,由x0≠0可得x2≠0,
∴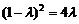 ,又
,又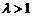 ,解得:
,解得: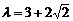 . ………………………………12分
. ………………………………12分
22、(本小题满分14分)
(1)∵ ,配方得
,配方得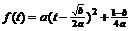 ,
,
由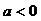 得最大值
得最大值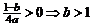 。……………………………………………3分
。……………………………………………3分
∴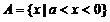 ,
,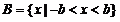 。
…………………………5分
。
…………………………5分
(2)要使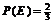 ,
,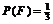 。可以使
。可以使
①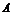 中有3个元素,
中有3个元素,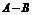 中有2个元素,
中有2个元素,
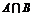 中有1个元素。
中有1个元素。
则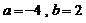 。 …………………………………………………………………8分
。 …………………………………………………………………8分
②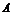 中有6个元素,
中有6个元素,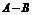 中有4个元素,
中有4个元素,
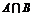 中有2个元素。
中有2个元素。
则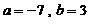 ……………………………………………………………………10分
……………………………………………………………………10分
(3)由(2)知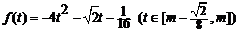 …………………………11分
…………………………11分
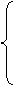
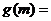
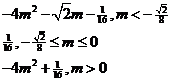 ……………………………………………14分
……………………………………………14分