
网址:http://www.1010jiajiao.com/paper/timu/5155516.html[举报]
20、(本题满分12分)
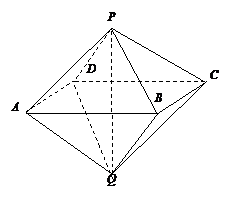 如图,已知两个正四棱锥P-ABCD与Q-ABCD的高分别为1和2,AB=4.
如图,已知两个正四棱锥P-ABCD与Q-ABCD的高分别为1和2,AB=4.
⑴ 证明PQ⊥平面ABCD;
⑵ 求异面直线AQ与PB所成的角;
⑶ 求点P到平面QAD的距离.
参考答案:
一、选择题(本大题共2小题,每小题5分,在每小题给出的四个选项中,只有一项是符合题目要求的)
|
题号 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
|
答案 |
B |
C |
B |
A |
B |
C |
A |
C |
D |
D |
D |
B |
简答与提示:
1、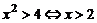 或
或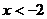 ,
,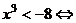
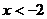 ;
;
2、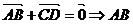
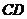 是平行四边形,
是平行四边形,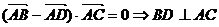 ;
;
3、根据题意: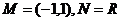 ;
;
4、根据对称性;
5、依题意: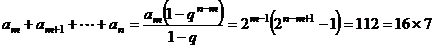 ;
;
6、根据线线、线面、面面平行和垂直的有关判定逐个判断即可;
7、①函数是偶函数,②函数先单调递增后单调递减,③当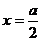 时,
时,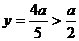 ;
;
8、a与b的夹角为60o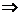
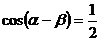 ,
,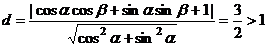 ;
;
9、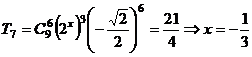 ,
,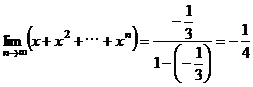 ;
;
10、乙丙丁所说为假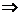 甲拿4,甲乙所说为假
甲拿4,甲乙所说为假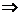 丙拿1,甲所说为假
丙拿1,甲所说为假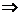 乙拿2;
乙拿2;
11、以正方体ABCD-A′B′C′D′的任意三个顶点为顶点可作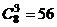 (个)三角形,正方体的表面及对角面每个面有
(个)三角形,正方体的表面及对角面每个面有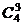 =4(个)三角形,所以所求概率为
=4(个)三角形,所以所求概率为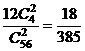 ;
;
12、椭圆+=1中,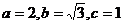 ,所以(|PnF|)min=
,所以(|PnF|)min=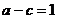 (|PnF|)max=
(|PnF|)max=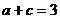
所以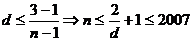 .
.
二、填空题(本大题共4小题,每小题4分,共16分,把答案填在横线上.)
13、0或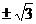 14、(-1,1)和(2,+∞)
14、(-1,1)和(2,+∞)
15、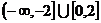 16、④
16、④
简答与提示:
13、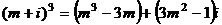 是纯虚数,则
是纯虚数,则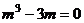 .
.
14、解:由f(x)的解析式可知f(x)图象连续及f(x)的单调性可确定:在(-1,1)和(2,+∞)上均有
f(x)>0.
15、命题p:不等式|x-m|+|x-1|>1的解集为R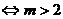 或
或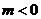
命题q:f(x)=log(3+m)x是(0,+∞)上的增函数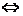 3+m>1
3+m>1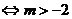
“p且q”是假命题,“p或q”是真命题说明命题p和q一真一假,
所以实数m的取值范围是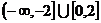 .
.
16、当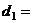
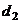 =0,①不对;若
=0,①不对;若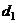 +
+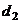 =0,点
=0,点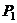 、
、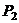 在直线
在直线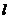 上或在直线
上或在直线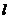 的异侧,所以②③错;
的异侧,所以②③错;
三、解答题
17:解:⑴ ∵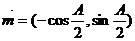 ,
,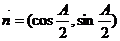 ,且
,且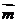 .
.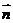 =,
=,
∴-cos2+sin2=, 即-cosA=, ……………………4分
又A∈(0,p),
∴A=p, …………………………………………………………6分
⑵ S△ABC=bc.sinA=b.c.sinp=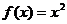 ,∴bc=4, …………………8分
,∴bc=4, …………………8分
又由余弦定理得:a2=b2+c2-2bc.cos120°=b2+c2+bc , ………10分
∴16=(b+c)2,故b+c=4. ……………………………………12分
18、解: ⑴ 由题意,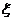 的可能取值为1,2,3,4,5
的可能取值为1,2,3,4,5
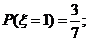
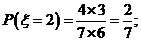
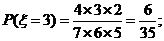
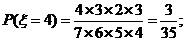
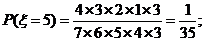 …………………………………………5分
…………………………………………5分
所以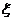 的分布列为:
的分布列为:
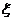 |
1 |
2 |
3 |
4 |
5 |
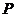 |
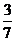 |
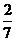 |
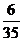 |
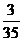 |
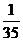 |
…………………………………………7分
⑵ 因为甲先取,所以甲只有可能在第1次,第3次和第5次取球,记”甲取到白球”为事件 ,则
,则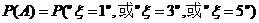
∵事件 两两互斥,
两两互斥,
∴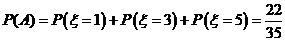 . ………………………………12分
. ………………………………12分
19.(本小题满分12分)
解:⑴ 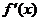 =-2x+a-
=-2x+a-
∵f(x)在(0,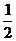 )上为减函数,∴x∈(0,
)上为减函数,∴x∈(0,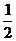 )时-2x+a-
)时-2x+a- <0恒成立。
<0恒成立。
即a<2x+ 恒成立。 …………………………………………………………2分
恒成立。 …………………………………………………………2分
设g(x)= 2x+ ,则
,则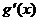 =2-
=2-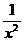
∵x∈(0,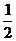 )时
)时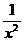 >4,∴
>4,∴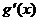 <0,∴g(x) 在(0,
<0,∴g(x) 在(0,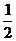 )上递减。
………4分
)上递减。
………4分
∴g(x) >g(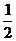 )=3,∴a≤3。
…………………………………………………6分
)=3,∴a≤3。
…………………………………………………6分
⑵
若f(x)既有极大值又有极小值,则首先必须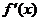 =0有两个不同正根x1 ,x2 ,
=0有两个不同正根x1 ,x2 ,
即 2x2-ax+1=0有两个不同正根。 …………8分
令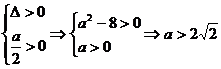
∴当a>2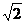 时,
时,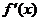 =0有两个不等的正根. ………………………10分
=0有两个不等的正根. ………………………10分
不妨设x1 <x2 ,由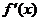 =-
=- (2x2-ax+1)=-
(2x2-ax+1)=-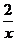 (x-x1)(x-x2)知:
(x-x1)(x-x2)知:
0<x<x1时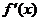 <0,x1<x<x2时
<0,x1<x<x2时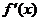 >0,x>x2时
>0,x>x2时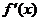 <0。
<0。
∴当a>2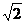 时f(x)既有极大值f(x2)又有极小值f(x1) . …………………12分
时f(x)既有极大值f(x2)又有极小值f(x1) . …………………12分
20.(本小题满分12分)
解法一:
⑴
连结AC、BD,设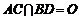 .由P-ABCD与Q-ABCD都是正四棱锥,
.由P-ABCD与Q-ABCD都是正四棱锥,
所以PO⊥平面ABCD,QO⊥平面ABCD.从而P、O、Q三点在一条直线上,
所以PQ⊥平面ABCD.
由题设知,ABCD是正方形,所以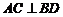 .
.
⑵ 由⑴,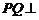 平面
平面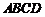 ,故可以分别以直线CA、DB、QP为
,故可以分别以直线CA、DB、QP为 轴,
轴,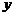 轴,
轴,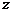 轴建立空间直角坐标系(如上图),由题设条件,相关各点的坐标分别是
轴建立空间直角坐标系(如上图),由题设条件,相关各点的坐标分别是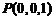 ,
,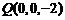 ,
,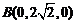 ,所以
,所以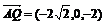 ,
,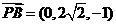 ,
,
于是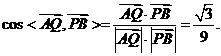
从而异面直线AQ与PB所成的角是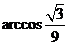 .
.
⑶ 由⑵,点D的坐标是(0,-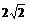 ,0),
,0),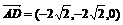 ,
,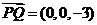 ,
,
设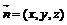 是平面QAD的一个法向量,
是平面QAD的一个法向量,
由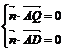 得
得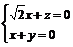 .取x=1,得
.取x=1,得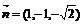 .
.
所以点P到平面QAD的距离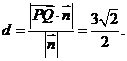 .
.
解法二:
⑴ 取AD的中点M,连结PM,QM.因为P-ABCD与Q-ABCD都是正四棱锥,
所以AD⊥PM,AD⊥QM. 从而AD⊥平面PQM.
又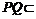 平面PQM,所以PQ⊥AD.同理PQ⊥AB,所以PQ⊥平面ABCD.
平面PQM,所以PQ⊥AD.同理PQ⊥AB,所以PQ⊥平面ABCD.
 ⑵ 连结AC、BD设
⑵ 连结AC、BD设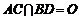 ,由PQ⊥平面ABCD及
,由PQ⊥平面ABCD及
正四棱锥的性质可知O在PQ上,从而P、A、Q、C四
点共面.取OC的中点N,连结PN.
因为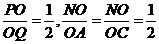 ,所以
,所以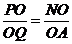 ,
,
从而AQ∥PN.∠BPN(或其补角)是异面直线AQ
与PB所成的角.连接BN,
因为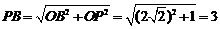 .
.
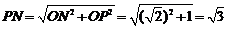
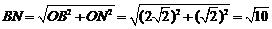
所以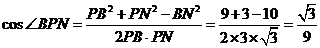 .
.
从而异面直线AQ与PB所成的角是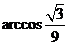 .
.
⑶ 由⑴知,AD⊥平面PQM,所以平面PQM⊥平面QAD. 过P作PH⊥QM于H,
则PH⊥平面QAD,所以PH的长为点P到平面QAD的距离.
连结OM,则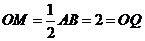 .所以
.所以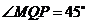 ,
,
又PQ=PO+QO=3,于是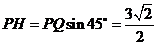 .
.
即点P到平面QAD的距离是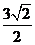 .
.
21.解:⑴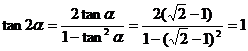 又∵
又∵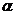 为锐角
为锐角
∴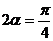 ∴
∴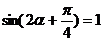
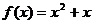 …………3分
…………3分
⑵ 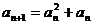 ∵
∵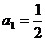 ∴
∴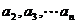 都大于0
都大于0
∴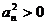 ∴
∴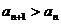 …………………………………7分
…………………………………7分
⑶ 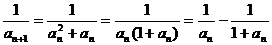
∴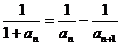 …………………………………8分
…………………………………8分
∴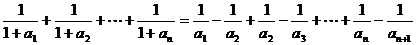
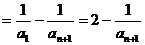 …………………………………10分
…………………………………10分
∵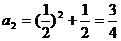 ,
,
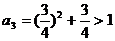 , 又∵
, 又∵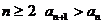
∴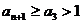 ∴
∴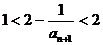
∴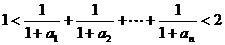 …………………………12分
…………………………12分
22.解:⑴ 设点M的坐标为(x,y)则由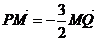 ,
,
得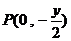 ,及
,及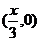
由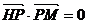 得
得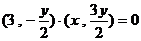 …………………3分
…………………3分
∴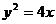 ,由点Q在x轴的正半轴上得
,由点Q在x轴的正半轴上得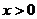
∴M点轨迹G方程: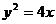 (
(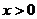 )
……………………5分
)
……………………5分
⑵ 设直线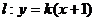 ,其中
,其中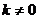 代入
代入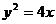
得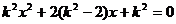 (1)
……………………6分
(1)
……………………6分
设A(x1,y1),B(x2,y2),则x1,x2是方程(1)的两个实数
∴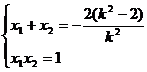 ∴AB中点坐标为
∴AB中点坐标为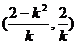
AB的垂直平分线为: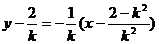 ,
……………………8分
,
……………………8分
令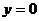 ,
,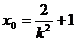 ∴点E的坐标为
∴点E的坐标为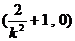
因为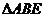 为正三角形
为正三角形
∴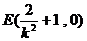 到直线AB的距离等于
到直线AB的距离等于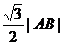 …………………10分
…………………10分
∴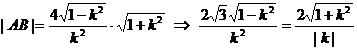 ……12分
……12分
∴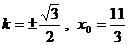 . …………………………………………14分
. …………………………………………14分