
网址:http://www.1010jiajiao.com/paper/timu/5155537.html[举报]
19.(本题满分14分,第(1)题6分,第(2)题8分)
据预测,某旅游景区游客人数在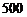 至
至 人之间,游客人数
人之间,游客人数 (人)与游客的消费总额
(人)与游客的消费总额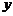 (元)之间近似地满足关系:
(元)之间近似地满足关系: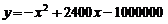 .
.
(1)若该景区游客消费总额不低于 元时,求景区游客人数的范围.
元时,求景区游客人数的范围.
(2)当景区游客的人数为多少人时,游客的人均消费最高?并求游客的人均最高消费额.
[解]
[解]
参考答案与评分标准(文科)
一、填空题
1.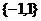 2.1
3.
2.1
3.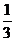 4.
4.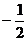 5.2
6.5
7.13
5.2
6.5
7.13
8.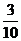 9.3
10.2
11.
9.3
10.2
11.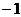 12.③④
12.③④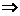 ①②或①④
①②或①④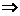 ②③
②③
二、选择题
13.B 14.A 15.D 16.A
三、解答题
17.解:由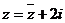 得:
得: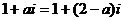 ,所以
,所以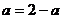 ,
,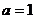 --------------4分
--------------4分
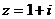 ,
,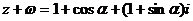 ------------------------------------------5分
------------------------------------------5分
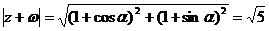 ---------------------------------------------7分
---------------------------------------------7分
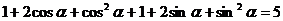 ,
,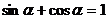 ----------------8分
----------------8分
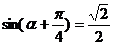 ------------------10分
------------------10分 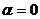 或
或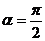 ------------------------12分
------------------------12分
18.解:(1)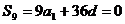 ,得:
,得: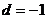 ,
,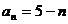 -------------------------3分
-------------------------3分
由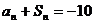 ,
,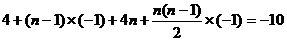
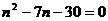 ,得到
,得到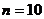 ---------------------------------------------6分
---------------------------------------------6分
(2)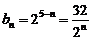 ,
,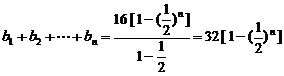 ,------9分
,------9分
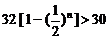 ,得
,得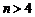 ,所以正整数
,所以正整数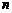 的最小值为
的最小值为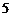 。---------------12分
。---------------12分
19.解:(1)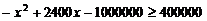
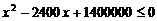 ,得
,得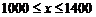 -------------------------------------4分
-------------------------------------4分
又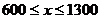 ,所以景区游客人数的范围是1000至1300人-------------6分
,所以景区游客人数的范围是1000至1300人-------------6分
(2)设游客的人均消费额为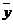 ,则
,则
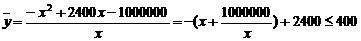 ---------------------12分
---------------------12分
当且仅当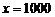 时等号成立。---------------------------------------------------------14分
时等号成立。---------------------------------------------------------14分
答:当景区游客的人数为 时,游客的人均消费最高,最高消费额为
时,游客的人均消费最高,最高消费额为 元。
元。
 20.解:(1)因为正子体的各个顶点是正方体
20.解:(1)因为正子体的各个顶点是正方体
各面的中心,所以
 -------------------------------------2分
-------------------------------------2分
正四棱锥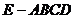 的底面积
的底面积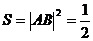 ,高
,高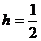 ---------------------------------5分
---------------------------------5分
正子体体积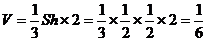 ---------------------------------------------7分
---------------------------------------------7分
(2)方法一:建立空间直角坐标系,评分标准见理科答案。
方法二:记正方体为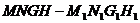 ,
,
记棱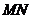 中点为
中点为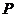 ,
,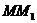 中点为
中点为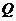 ----------------------------------------------------------8分
----------------------------------------------------------8分
则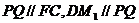 ,所以
,所以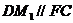 -------------------------------------------------10分
-------------------------------------------------10分
异面直线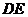 与
与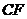 所成的角即为
所成的角即为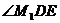 ------------------------------------------------11分
------------------------------------------------11分
又因为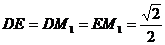 ,故
,故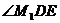 =
=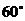 ------------------------------------14分
------------------------------------14分
异面直线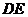 与
与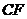 所成的角为
所成的角为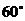 。
。
21.解:(1)∵对任意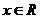 ,
,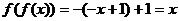 ,∴
,∴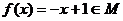 --2分
--2分
∵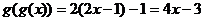 不恒等于
不恒等于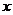 ,∴
,∴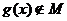 --------------------------4分
--------------------------4分
(2)设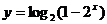
由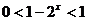 解得:
解得: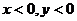 ----------------------------------------------------6分
----------------------------------------------------6分
由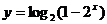
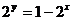 ,反函数为
,反函数为 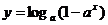 ,
, -------8分
-------8分
∵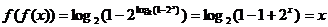
∴ --------------------------------------------------------------------11分
--------------------------------------------------------------------11分
(3)∵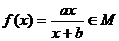 ,∴
,∴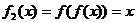 对一切定义域中
对一切定义域中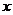 恒成立。
恒成立。
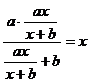 ,解得:
,解得: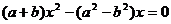 恒成立,故
恒成立,故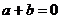 ----------13分
----------13分
由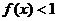 ,得到
,得到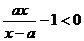 ,
,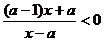 ,由
,由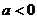 ,
,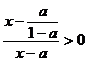 --14分
--14分
 -------------15分,故
-------------15分,故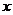 的范围为:
的范围为: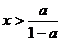 或
或 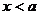 -------------16分
-------------16分
22.解:(1)把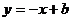 代入
代入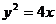 得
得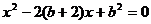 。
。
令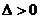 ,得
,得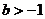 。
---------------------------------------------------------------------------2分
。
---------------------------------------------------------------------------2分
设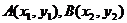 ,则
,则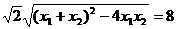 -------------------------------4分
-------------------------------4分
∴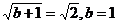 , ∴直线的方程为y= -x+1。
------------------------------------6分
, ∴直线的方程为y= -x+1。
------------------------------------6分
(2)设D (1 , y0),代入y 2= 4x,得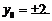 因此得到D点坐标:D (1,2 ) 或D′(1,-2)
因此得到D点坐标:D (1,2 ) 或D′(1,-2)
点D(D′)到直线y=-x+1的距离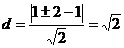 .
----------------------------------------8分
.
----------------------------------------8分
∴∆DAB的面积为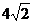 。------------------------------------------------------------------------10分
。------------------------------------------------------------------------10分
(3)设与直线y=-x+1平行且与y2 = 4 x相切的直线为y=-x+t, 代入y 2 =4 x,
得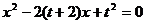 ,令∆=0,得
,令∆=0,得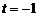 ,此时切点为
,此时切点为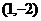 。
。
另解:设与直线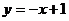 平行且距离为
平行且距离为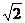 的直线为y=-x+t, 得
的直线为y=-x+t, 得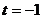 或3------12分
或3------12分
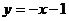 与 y 2 = 4 x的交点仅有一个为
与 y 2 = 4 x的交点仅有一个为 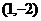 ,
,
y = - x +3与y 2 = 4 x的交点为 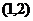 ,
,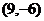 。
。
y=-x+1与y2=4x的交点为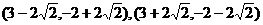
∴当 时,
时,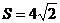 ---------------------------------------------------------14分
---------------------------------------------------------14分
当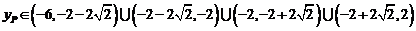 时,
时,
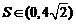 --------------------------------------------------------------------------------------16分
--------------------------------------------------------------------------------------16分
当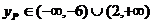 时,
时,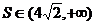 。-------------------------------------18分
。-------------------------------------18分