
网址:http://www.1010jiajiao.com/paper/timu/5155611.html[举报]
10.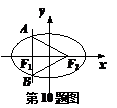 已知点F1、F2分别是椭圆
已知点F1、F2分别是椭圆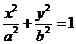 的左、右焦点,过F1且垂直于x轴的直线与椭圆交于A、B两点,若△ABF2为正三角形,则该椭圆的离心率
的左、右焦点,过F1且垂直于x轴的直线与椭圆交于A、B两点,若△ABF2为正三角形,则该椭圆的离心率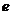 为( ).
为( ).
|
|
A. 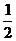 |
B . 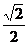 |
C.
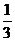 |
D . 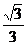 |
数学试题参考答案和评分标准(文科1)
一、选择题(每题5分,共40分)
|
序号 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
答案 |
C |
D |
D |
A |
C |
B |
A |
B |
C |
D |
二、填空题(每题5分,共30分)
11.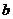 <
< <
<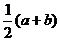 12.
12. 13.
13.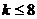
14.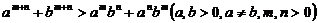 (或
(或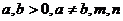 为正整数)注:填
为正整数)注:填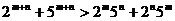 以及是否注明字母的取值符号和关系,均不扣分.
以及是否注明字母的取值符号和关系,均不扣分.
三、解答题(满分80分,解答应写出文字说明和演算步骤).
15. 解:∵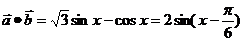 , ……………………………………………4分
, ……………………………………………4分
∴当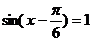 即
即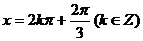 时,
……………………………………………6分
时,
……………………………………………6分
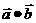 取得最大值2. ……………………………………………………………………………………………8分
取得最大值2. ……………………………………………………………………………………………8分
此时,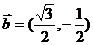 ,故
,故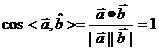 ,………………………………………11分
,………………………………………11分
∴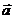 和
和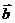 的夹角是0. …………………………………………………………………………………………12分
的夹角是0. …………………………………………………………………………………………12分
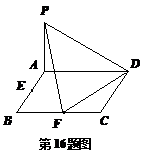 注:也可以由
注:也可以由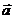 和
和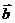 同向来说明.
同向来说明.
16.解:(1) 证明:连结AF,
∵在矩形ABCD中,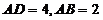 ,F是线段BC的中点,
,F是线段BC的中点,
∴AF⊥FD. …………………………………………………………………3分
又∵PA⊥面ABCD,∴PA⊥FD. …………………………………4分
∴平面PAF⊥FD. …………………………………………………………5分
∴PF⊥FD. …………………………………………………………………6分
(2) 过E作EH∥FD交AD于H,则EH∥平面PFD且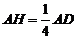 . …………9分
. …………9分
再过H作HG∥DP交PA于G,则HG∥平面PFD且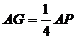 . ……………11分
. ……………11分
∴平面EHG∥平面PFD.
∴EG∥平面PFD. ……………………………………………………………………………………………13分
从而满足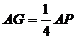 的点G为所找.
………………………………………………………………14分
的点G为所找.
………………………………………………………………14分
注:1. 也可以延长DF、AB交于R,然后找EG∥PR进行处理)
2. 本题也可用向量法解.
17.解:将圆C的方程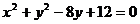 配方得标准方程为
配方得标准方程为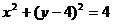 ,则此圆的圆心为(0 , 4),半径为2.
,则此圆的圆心为(0 , 4),半径为2.
(1) 若直线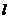 与圆C相切,则有
与圆C相切,则有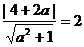 . ………………………………………………3分
. ………………………………………………3分
解得 . ……………………………………………………………………………………………………5分
. ……………………………………………………………………………………………………5分
(2) 解法一:过圆心C作CD⊥AB,则根据题意和圆的性质,得
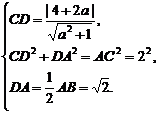 ……………………………………………………………………………8分
……………………………………………………………………………8分
解得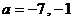 . ………………………………………………………………………………………………10分
. ………………………………………………………………………………………………10分
(解法二:联立方程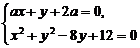 并消去
并消去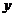 ,得
,得
 .
.
设此方程的两根分别为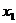 、
、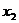 ,则用
,则用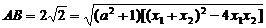 即可求出a.)
即可求出a.)
∴直线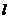 的方程是
的方程是 和
和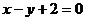 . ………………………………………12分
. ………………………………………12分
18.解:(1)由 ,令
,令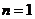 ,则
,则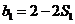 ,又
,又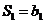 ,所以
,所以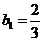 .
.
由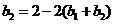 ,得
,得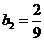 .
.
由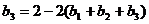 ,得
,得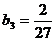 . ……………………………………………………………………3分
. ……………………………………………………………………3分
(2)方法一:当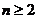 时,由
时,由 ,可得
,可得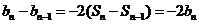 .
.
即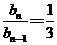 . …………………………………………………………………………………………………………………………5分
. …………………………………………………………………………………………………………………………5分
所以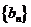 是以
是以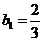 为首项,
为首项,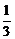 为公比的等比数列,于是
为公比的等比数列,于是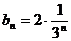 . ……………6分
. ……………6分
方法二:由(1)归纳可得,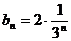 ,它适合
,它适合 .
.
所以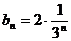 . ……………………………………………………………………………………………………………5分
. ……………………………………………………………………………………………………………5分
注:方法二扣1分.
(3)数列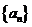 为等差数列,公差
为等差数列,公差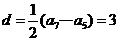 ,可得
,可得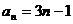 . ……………8分
. ……………8分
从而 ,………………………………………………9分
,………………………………………………9分
∴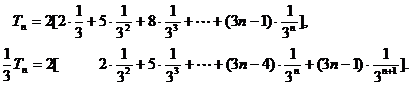 ……………10分
……………10分
∴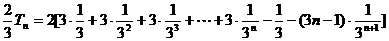 .
…………………11分
.
…………………11分
∴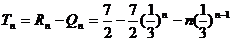 .
……………………………………………………………14分
.
……………………………………………………………14分
19.解:(1) 由表中可以看出,所选出的8位同学中,数学和物理分数均为优秀的人数是3人,其概率是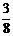 . ………………………………………………………………………………………………………3分
. ………………………………………………………………………………………………………3分
(2) 变量y与x、z与x的相关系数分别是
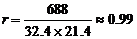 、
、 . ……………………………………………5分
. ……………………………………………5分
可以看出,物理与数学、化学与数学的成绩都是高度正相关. …………………………6分
(3) 设y与x、z与x的线性回归方程分别是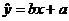 、
、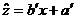 .
.
根据所给的数据,可以计算出 ,
,
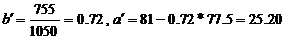 . ……………………………………………………10分
. ……………………………………………………10分
所以y与x和z与x的回归方程分别是
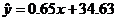 、
、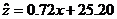 . …………………………………………………………11分
. …………………………………………………………11分
又y与x、z与x的相关指数是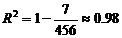 、
、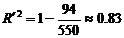 . ……13分
. ……13分
故回归模型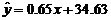 比回归模型
比回归模型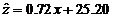 的拟合的效果好. …14分
的拟合的效果好. …14分
20.解:(1)
易知,函数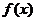 的定义域为
的定义域为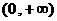 . ……………………………………………1分
. ……………………………………………1分
当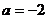 时,
时,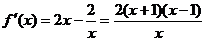 . ……………………………………………2分
. ……………………………………………2分
当x变化时, 和
和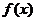 的值的变化情况如下表: ……………………………………4分
的值的变化情况如下表: ……………………………………4分
|
x |
(0,1) |
1 |
(1,+∞) |
 |
- |
0 |
+ |
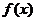 |
递减 |
极小值 |
递增 |
由上表可知,函数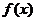 的单调递减区间是(0,1)、单调递增区间是(1,+∞)、极小值是
的单调递减区间是(0,1)、单调递增区间是(1,+∞)、极小值是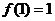 . ……………………………………………………………………………………………………………7分
. ……………………………………………………………………………………………………………7分
(2) 由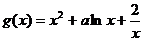 ,得
,得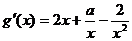 . ………………………………8分
. ………………………………8分
又函数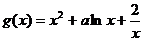 为
为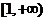 上单调函数,
上单调函数,
① 若函数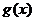 为
为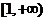 上的单调增函数,则
上的单调增函数,则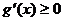 在
在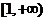 上恒成立,即不等式
上恒成立,即不等式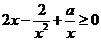 在
在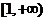 上恒成立.也即
上恒成立.也即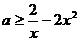 在
在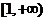 上恒成立. ………11分
上恒成立. ………11分
又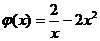 在
在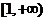 上为减函数,
上为减函数,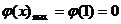 . ……………………12分
. ……………………12分
所以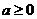 .
.
② 若函数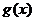 为
为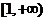 上的单调减函数,则
上的单调减函数,则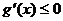 在
在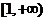 上恒成立,这是不可能的. ……………………………………………………………………………………………………………………13分
上恒成立,这是不可能的. ……………………………………………………………………………………………………………………13分
综上,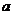 的取值范围为
的取值范围为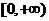 . ………………………………………………………………………14分
. ………………………………………………………………………14分