
网址:http://www.1010jiajiao.com/paper/timu/5156230.html[举报]
18.(本小题满分12分)
甲、乙两名跳高运动员一次试跳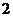 米高度成功的概率分别是
米高度成功的概率分别是 ,
, ,且每次试跳成功与否相互之间没有影响,求:
,且每次试跳成功与否相互之间没有影响,求:
(Ⅰ)甲试跳三次,第三次才成功的概率;
(Ⅱ)甲、乙两人在第一次试跳中至少有一人成功的概率;
(Ⅲ)甲、乙各试跳两次,甲比乙的成功次数恰好多一次的概率.
参考答案
一、选择题:本大题考查基本概念和基本运算,每小题5分,满分60分.
1.C 2.C 3.D 4.A 5.A 6.B
7.D 8.B 9.D 10.B 11.B 12.C
二、填空题:本大题考查基础知识和基本运算.每小题4分,满分16分.
13. 14.
14.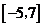 15.
15.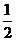
16.答案不唯一,如“图形的全等”、“图形的相似”、“非零向量的共线”、“命题的充要条件”等等.
三、解答题:本大题共6小题,共74分.解答应写出文字说明,证明过程或演算步骤.
17.本小题主要考查两角和差公式,用同角三角函数关系等解斜三角形的基本知识以及推理和运算能力.满分12分.
解:(Ⅰ) ,
,
 .
.
又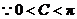 ,
, .
.
(Ⅱ)由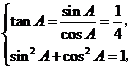 且
且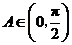 ,
,
得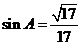 .
. ,
,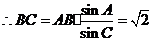 .
.
18.本小题主要考查概率的基础知识,运用数学知识解决问题的能力,以及推理与运算能力.满分12分.
解:记“甲第 次试跳成功”为事件
次试跳成功”为事件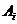 ,“乙第
,“乙第 次试跳成功”为事件
次试跳成功”为事件 ,依题意得
,依题意得 ,
, ,且
,且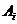 ,
, (
(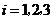 )相互独立.
)相互独立.
(Ⅰ)“甲第三次试跳才成功”为事件 ,且三次试跳相互独立,
,且三次试跳相互独立,
 .
.
答:甲第三次试跳才成功的概率为 .
.
(Ⅱ)“甲、乙两人在第一次试跳中至少有一人成功”为事件 .
.
解法一: ,且
,且 ,
,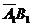 ,
, 彼此互斥,
彼此互斥,



 .
.
解法二: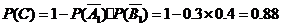 .
.
答:甲、乙两人在第一次试跳中至少有一人成功的概率为 .
.
(Ⅲ)设“甲在两次试跳中成功 次”为事件
次”为事件 ,
,
“乙在两次试跳中成功 次”为事件
次”为事件 ,
,
 事件“甲、乙各试跳两次,甲比乙的成功次数恰好多一次”可表示为
事件“甲、乙各试跳两次,甲比乙的成功次数恰好多一次”可表示为 ,且
,且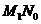 ,
,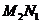 为互斥事件,
为互斥事件,
 所求的概率为
所求的概率为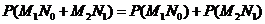

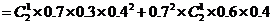
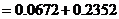

答:甲、乙每人试跳两次,甲比乙的成功次数恰好多一次的概率为 .
.
19.本小题主要考查直线与平面的位置关系,二面角的大小等知识,考查空间想象能力、逻辑思维能力和运算能力.满分12分.
解法一:(Ⅰ)取 中点
中点 ,连结
,连结 .
.
 为正三角形,
为正三角形,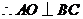 .
.
 正三棱柱
正三棱柱 中,平面
中,平面 平面
平面 ,
, 平面
平面 .
.
 连结
连结 ,在正方形
,在正方形 中,
中, 分别为
分别为
 的中点,
的中点,
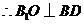 ,
,
 .
.
在正方形 中,
中,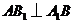 ,
,
 平面
平面 .
.
(Ⅱ)设 与
与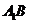 交于点
交于点 ,在平面
,在平面 中,
中,
作 于
于 ,连结
,连结 ,由(Ⅰ)得
,由(Ⅰ)得 平面
平面 .
.
 ,
,
 为二面角
为二面角 的平面角.
的平面角.
在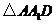 中,由等面积法可求得
中,由等面积法可求得 ,
,
又 ,
,

 .
.
所以二面角 的大小为
的大小为 .
.
解法二:(Ⅰ)取 中点
中点 ,连结
,连结 .
.
 为正三角形,
为正三角形,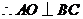 .
.
 在正三棱柱
在正三棱柱 中,
中,
平面 平面
平面 ,
,
 平面
平面 .
.
取 中点
中点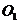 ,以
,以 为原点,
为原点, ,
, ,
, 的方向为
的方向为 轴的正方向建立空间直角坐标系,则
轴的正方向建立空间直角坐标系,则 ,
, ,
, ,
, ,
, ,
,
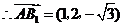 ,
, ,
, .
.
 ,
,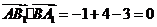 ,
,
 ,
, .
.
 平面
平面 .
.
(Ⅱ)设平面 的法向量为
的法向量为 .
.
 ,
, .
.
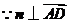 ,
, ,
,



令 得
得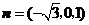 为平面
为平面 的一个法向量.
的一个法向量.
由(Ⅰ)知 平面
平面 ,
,
 为平面
为平面 的法向量.
的法向量.
 ,
, .
.
 二面角
二面角 的大小为
的大小为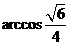 .
.
20.本题主要考查函数的单调性、极值以及函数导数的应用,考查运用数学知识分析问题解决问题的能力.满分12分.
解:(Ⅰ)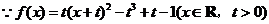 ,
,
 当
当 时,
时, 取最小值
取最小值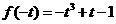 ,
,
即 .
.
(Ⅱ)令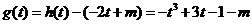 ,
,
由 得
得 ,
, (不合题意,舍去).
(不合题意,舍去).
当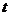 变化时
变化时 ,
, 的变化情况如下表:
的变化情况如下表:
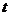 |
 |
 |
 |
 |
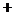 |
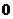 |
 |
 |
递增 |
极大值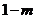 |
递减 |
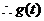 在
在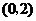 内有最大值
内有最大值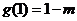 .
.
 在
在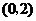 内恒成立等价于
内恒成立等价于 在
在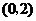 内恒成立,
内恒成立,
即等价于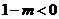 ,
,
所以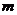 的取值范围为
的取值范围为 .
.
21.本小题考查数列的基本知识,考查等比数列的概念、通项公式及数列的求和,考查分类讨论及化归的数学思想方法,以及推理和运算能力.满分12分.
解:(Ⅰ) ,
,
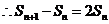 ,
,
 .
.
又 ,
,
 数列
数列 是首项为
是首项为 ,公比为
,公比为 的等比数列,
的等比数列,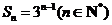 .
.
当 时,
时, ,
,
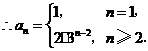
(Ⅱ) ,
,
当 时,
时, ;
;
当 时,
时,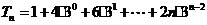 ,…………①
,…………①
 ,………………………②
,………………………②
 得:
得:
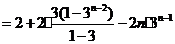
 .
.
 .
.
又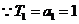 也满足上式,
也满足上式,
 .
.
22.本小题主要考查直线、抛物线、向量等基础知识,考查轨迹方程的求法以及研究曲线几何特征的基本方法,考查运算能力和综合解题能力.满分14分.
解法一:(Ⅰ)设点 ,则
,则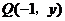 ,由
,由 得:
得:
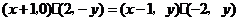 ,化简得
,化简得 .
.
(Ⅱ)(1)设直线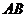 的方程为:
的方程为:
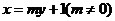 .
.
设 ,
,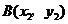 ,又
,又 ,
,
 联立方程组
联立方程组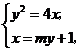 ,消去
,消去 得:
得: ,
,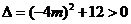 ,
,

由 ,
, 得:
得:
 ,
, ,整理得:
,整理得:
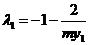 ,
, ,
,
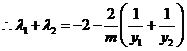
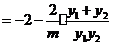

 .
.
解法二:(Ⅰ)由 得:
得: ,
,
 ,
,
 ,
,
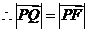 .
.
所以点 的轨迹
的轨迹 是抛物线,由题意,轨迹
是抛物线,由题意,轨迹 的方程为:
的方程为: .
.
(Ⅱ)(1)由已知 ,
, ,得
,得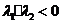 .
.
则: .…………①
.…………①
过点 分别作准线
分别作准线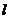 的垂线,垂足分别为
的垂线,垂足分别为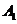 ,
,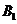 ,
,
则有: .…………②
.…………②
由①②得: ,即
,即 .
.
(Ⅱ)(2)解:由解法一,



 .
.
当且仅当 ,即
,即 时等号成立,所以
时等号成立,所以 最小值为
最小值为 .
.