网址：http://www.1010jiajiao.com/paper/timu/5156466.html[举报]

11、为研究“原函数图象与其反函数图象的交点是否在直线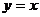上”这个课题，我们可以分三步进行研究：

　　 (I)首先选取如下函数：

　　 ，，

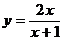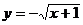
　　 求出以上函数图象与其反函数图象的交点坐标：

　　 与其反函数的交点坐标为(－1，－1)

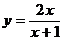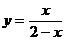　　 与其反函数的交点坐标为(0，0)，(1，1)

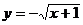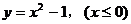　　 与其反函数的交点坐标为()，(－1，0)，(0，－1)

　　 (II)观察分析上述结果得到研究结论；

　　 (III)对得到的结论进行证明。

　　 现在，请你完成(II)和(III)。

解：(II)原函数图象与其反函数图象的交点不一定在直线y＝x上　　　　　 2分

　　 (III)证明：设点(a，b)是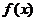的图象与其反函数图象的任一交点，由于原函数与反函数图象关于直线y＝x对称，则点(b，a)也是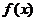的图象与其反函数图象的交点，且有

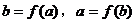
　　 若a＝b时，交点显然在直线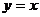上

　　 若a<b且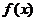是增函数时，有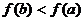，从而有b<a，矛盾；若b<a且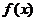是增函数时，有，从而有a<b，矛盾

　　 若a<b且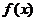是减函数，有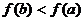，从而a<b成立，此时交点不在直线y＝x上；同理，b<a且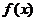是减函数时，交点也不在直线y＝x上。

　　 综上所述，如果函数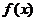是增函数，并且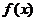的图象与其反函数的图象有交点，则交点一定在直线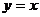上；

　　 如果函数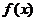是减函数，并且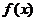的图象与其反函数的图象有交点，则交点不一定在直线y＝x上。　　　　　　　　　 　　　　　　　　　　　　　　　　　　　　　 14分