
网址:http://www.1010jiajiao.com/paper/timu/5156555.html[举报]
13)与椭圆 具有相同的离心率且过点(2,-
具有相同的离心率且过点(2,-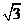 )的椭圆的标准方程是_____
)的椭圆的标准方程是_____
14)离心率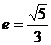 ,一条准线为
,一条准线为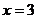 的椭圆的标准方程是_______。
的椭圆的标准方程是_______。
15)过抛物线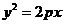 (p>0)的焦点F作一直线l与抛物线交于P、Q两点,作PP1、QQ1垂直于抛物线的准线,垂足分别是P1、Q1,已知线段PF、QF的长度分别是a、b,那么|P1Q1|= 。
(p>0)的焦点F作一直线l与抛物线交于P、Q两点,作PP1、QQ1垂直于抛物线的准线,垂足分别是P1、Q1,已知线段PF、QF的长度分别是a、b,那么|P1Q1|= 。
16)若直线l过抛物线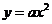 (a>0)的焦点,并且与y轴垂直,若l被抛物线截得的线段长为4,则a=_______。
(a>0)的焦点,并且与y轴垂直,若l被抛物线截得的线段长为4,则a=_______。
答案
13、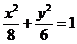 或
或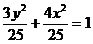 。14、
。14、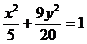
15、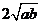
16、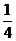
17、解:由已知条件得椭圆的焦点在x轴上,其中c=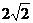 ,a=3,从而b=1,所以其标准方程是:
,a=3,从而b=1,所以其标准方程是:
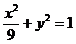 .联立方程组
.联立方程组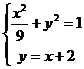 ,消去y得,
,消去y得,  .
.
设A(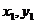 ),B(
),B(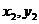 ),AB线段的中点为M(
),AB线段的中点为M(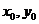 )那么:
)那么: 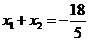 ,
,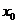 =
=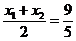
所以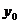 =
=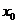 +2=
+2=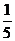 .
.
也就是说线段AB中点坐标为(-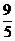 ,
,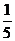 ).
).
18、解:由于椭圆焦点为F(0,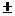 4),离心率为e=
4),离心率为e=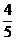 ,所以双曲线的焦点为F(0,
,所以双曲线的焦点为F(0,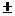 4),离心率为2,
4),离心率为2,
从而c=4,a=2,b=2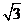 .
.
所以求双曲线方程为: 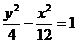
19、解:由于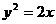 ,
,
而|PA|=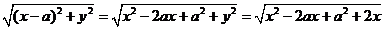
=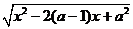 =
=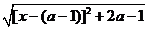 ,其中x
,其中x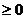
(1)a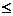 1时,当且仅当x=0时,
1时,当且仅当x=0时, 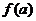 =|PA|min=|a|.
=|PA|min=|a|.
(2)a>时, 当且仅当x=a-1时, 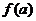 =|PA|min=
=|PA|min=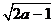 .
.
所以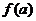 =
=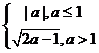
20、解:设双曲线方程为x2-4y2=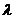 .
.
联立方程组得:
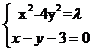 ,消去y得,3x2-24x+(36+
,消去y得,3x2-24x+(36+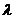 )=0
)=0
设直线被双曲线截得的弦为AB,且A(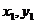 ),B(
),B(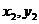 ),那么:
),那么:
那么:|AB|=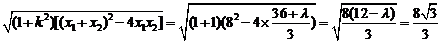
解得: 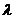 =4,所以,所求双曲线方程是:
=4,所以,所求双曲线方程是: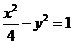
21、解:(1)联立方程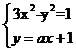 ,消去y得:(3-a2)x2-2ax-2=0.
,消去y得:(3-a2)x2-2ax-2=0.
设A(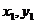 ),B(
),B(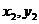 ),那么:
),那么: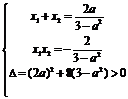 。
。
由于以AB线段为直径的圆经过原点,那么: ,即
,即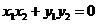 。
。
所以: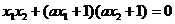 ,得到:
,得到: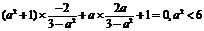 ,解得a=
,解得a=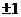
(2)假定存在这样的a,使A(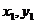 ),B(
),B(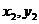 )关于直线
)关于直线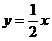 对称。
对称。
那么: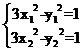 ,两式相减得:
,两式相减得: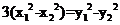 ,从而
,从而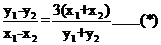
因为A(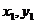 ),B(
),B(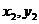 )关于直线
)关于直线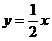 对称,所以
对称,所以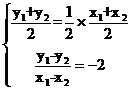
代入(*)式得到:-2=6,矛盾。
也就是说:不存在这样的a,使A(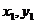 ),B(
),B(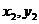 )关于直线
)关于直线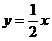 对称。
对称。