
网址:http://www.1010jiajiao.com/paper/timu/5156743.html[举报]
7.(人教A版选修2-1第67页例5)
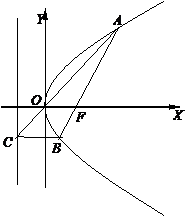
过抛物线焦点F的直线交抛物线于A,B两点,通过点A和抛物线顶点的直线交抛物线的准线于点D,求证:直线DB平行于抛物线的对称轴.
 变式(2001年全国卷):设抛物线
变式(2001年全国卷):设抛物线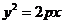 (
(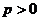 )的焦点为 F,经过点 F的直线交抛物线于A、B两点.点 C在抛物线的准线上,且BC∥X轴.证明直线AC经过原点O.
)的焦点为 F,经过点 F的直线交抛物线于A、B两点.点 C在抛物线的准线上,且BC∥X轴.证明直线AC经过原点O.
证明1:因为抛物线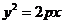 (
(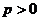 )的焦点为
)的焦点为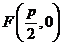 ,所以经过点F的直线AB的方程可设为
,所以经过点F的直线AB的方程可设为
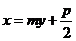 ,代人抛物线方程得
,代人抛物线方程得
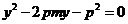 .
.
若记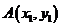 ,
,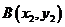 ,则
,则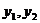 是该方程的两个根,所以
是该方程的两个根,所以
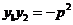 .
.
因为BC∥X轴,且点C在准线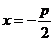 上,所以点C的坐标为
上,所以点C的坐标为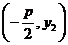 ,
,
 故直线CO的斜率为
故直线CO的斜率为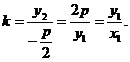
即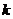 也是直线OA的斜率,所以直线AC经过原点O.
也是直线OA的斜率,所以直线AC经过原点O.
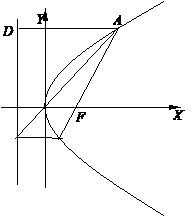
证明2:如图,记X轴与抛物线准线L的交点为E,
过A作AD⊥L,D是垂足.则
AD∥FE∥BC.
连结AC,与EF相交于点N,则
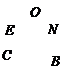
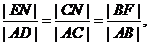
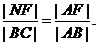
根据抛物线的几何性质,|AF|=|AD|,|BF|=|BC| ,
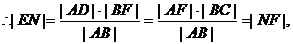
即点N是EF的中点,与抛物线的顶点O重合,所以直线AC经过原点O.