
网址:http://www.1010jiajiao.com/paper/timu/5156755.html[举报]
22.(本小题满分14分)
解:(Ⅰ)设椭圆的半焦距为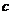 ,依题意
,依题意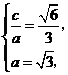
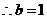 ,
,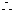 所求椭圆方程为
所求椭圆方程为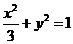 .
.
(Ⅱ)设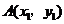 ,
,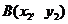 .
.
(1)当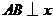 轴时,
轴时,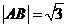 .
.
(2)当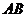 与
与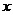 轴不垂直时,
轴不垂直时,
设直线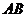 的方程为
的方程为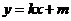 .
.
由已知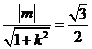 ,得
,得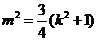 .
.
把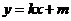 代入椭圆方程,整理得
代入椭圆方程,整理得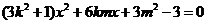 ,
,
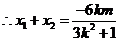 ,
,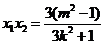 .
.
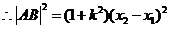

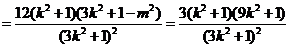
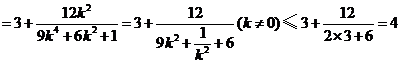 .
.
当且仅当 ,即
,即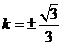 时等号成立.当
时等号成立.当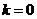 时,
时,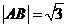 ,
,
综上所述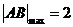 .
.
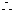 当
当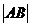 最大时,
最大时,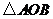 面积取最大值
面积取最大值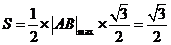 .
.
山东理
(13)设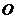 是坐标原点,
是坐标原点,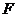 是抛物线
是抛物线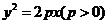 的焦点,
的焦点,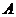 是抛物线上的一点,
是抛物线上的一点, 与
与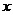 轴正向的夹角为
轴正向的夹角为 ,则
,则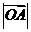 为
.
为
.
(21)(本小题满分12分)
已知椭圆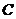 的中心在坐标原点,焦点在
的中心在坐标原点,焦点在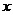 轴上,椭圆
轴上,椭圆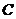 上的点到焦点距离的最大值为
上的点到焦点距离的最大值为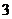 ,最小值为
,最小值为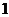 .
.
(Ⅰ)求椭圆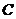 的标准方程;
的标准方程;
(Ⅱ)若直线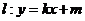 与椭圆
与椭圆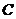 相交于
相交于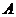 ,
,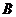 两点(
两点(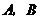 不是左右顶点),且以
不是左右顶点),且以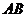 为直径的圆过椭圆
为直径的圆过椭圆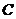 的右顶点,求证:直线
的右顶点,求证:直线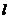 过定点,并求出该定点的坐标.
过定点,并求出该定点的坐标.
[标准答案](I)由题意设椭圆的标准方程为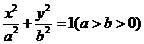
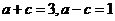 ,
,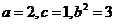
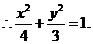
(II)设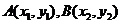 ,由
,由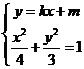 得
得
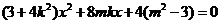 ,
,
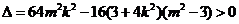 ,
,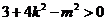 .
.


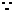 以AB为直径的圆过椭圆的右顶点
以AB为直径的圆过椭圆的右顶点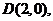
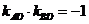 ,
,
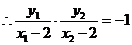 ,
,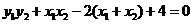 ,
,
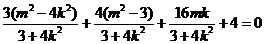 ,
,
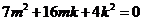 ,解得
,解得
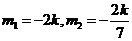 ,且满足
,且满足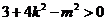 .
.
当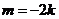 时,
时,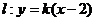 ,直线过定点
,直线过定点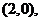 与已知矛盾;
与已知矛盾;
当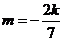 时,
时,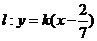 ,直线过定点
,直线过定点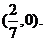
综上可知,直线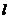 过定点,定点坐标为
过定点,定点坐标为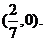
全国2理