20．(本小题满分14分)
已知正三角形的三个顶点都在抛物线上，其中为坐标原点，设圆是的内接圆(点为圆心)
(I)求圆的方程；
(II)设圆的方程为，过圆上任意一点分别作圆的两条切线，切点为，求的最大值和最小值．
本小题主要考查平面向量，圆与抛物线的方程及几何性质等基本知识，考查综合运用解析几何知识解决问题的能力．满分14分．
(I)解法一：设两点坐标分别为，，由题设知
．
解得，
所以，或，．
设圆心的坐标为，则，所以圆的方程为
．................................................................................. 4分
解法二：设两点坐标分别为，，由题设知
．
又因为，，可得．即
．
由，，可知，故两点关于轴对称，所以圆心在轴上．
设点的坐标为，则点坐标为，于是有，解得，所以圆的方程为．................................................................................. 4分
(II)解：设，则
．................................ 8分
在中，，由圆的几何性质得
，，
所以，由此可得
．
则的最大值为，最小值为．
江西理
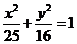上一点
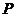到左准线的距离为10，
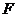是该椭圆的左焦点，若点
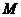满足
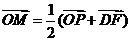，则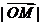
=
．