14．(湖北理科21)(本小题满分14分)
已知m，n为正整数.
(Ⅰ)用数学归纳法证明：当x>-1时，(1+x)m≥1+mx；
(Ⅱ)对于n≥6，已知，求证，m=1,1,2…，n；
(Ⅲ)求出满足等式3n+4m+…+(n+2)m=(n+3)n的所有正整数n.
解：(Ⅰ)证：当x=0或m=1时，原不等式中等号显然成立，下用数学归纳法证明：
当x>-1，且x≠0时，m≥2,(1+x)m>1+mx.
1
(i)当m=2时，左边＝1+2x+x2,右边＝1+2x，因为x≠0,所以x2>0，即左边>右边，不等式①成立；
(ii)假设当m=k(k≥2)时，不等式①成立，即(1+x)k>1+kx,则当m=k+1时，因为x>-1,所以1+x>0.又因为x≠0,k≥2,所以kx2>0.
于是在不等式(1+x)k>1+kx两边同乘以1+x得
(1+x)k.(1+x)>(1+kx)(1+x)=1+(k+1)x+kx2>1+(k+1)x,
所以(1+x)k+1>1+(k+1)x,即当m＝k+1时，不等式①也成立.
综上所述，所证不等式成立.
(Ⅱ)证：当
而由(Ⅰ)，
(Ⅲ)解：假设存在正整数成立，
即有()+＝1. ②
又由(Ⅱ)可得
()+
+与②式矛盾，
故当n≥6时，不存在满足该等式的正整数n.
故只需要讨论n=1,2,3,4,5的情形；
当n=1时，3≠4，等式不成立；
当n=2时，32+42＝52，等式成立；
当n=3时，33+43+53＝63，等式成立；
当n=4时，34+44+54+64为偶数，而74为奇数，故34+44+54+64≠74,等式不成立；
当n=5时，同n=4的情形可分析出，等式不成立.
综上，所求的n只有n=2,3.
15(湖南理科2)．不等式的解集是( D )
A． B． C． D．
16(湖南理科14)．设集合，，，
(1)的取值范围是
；
(2)若，且的最大值为9，则的值是
．
(1)(2)
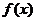为R上的减函数，则满足
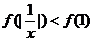的实数
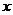的取值范围是(C)
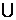(0，1)
D．(－
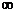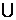，－1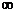)