
网址:http://www.1010jiajiao.com/paper/timu/5157193.html[举报]
20.(本小题满分12分)
已知函数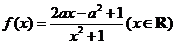 ,其中
,其中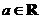 .
.
(Ⅰ)当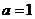 时,求曲线
时,求曲线 在点
在点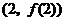 处的切线方程;
处的切线方程;
(Ⅱ)当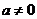 时,求函数
时,求函数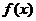 的单调区间与极值.
的单调区间与极值.
数学(理工类)参考解答
一、选择题:本题考查基本知识和基本运算.每小题5分,满分50分.
1.C 2.B 3.A 4.D 5.C
6.D 7.B 8.B 9.A 10.A
二、填空题:本题考查基本知识和基本运算.每小题4分,满分24分.
11.2 12.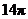 13.3
13.3
14.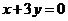 15.
15.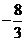 16.390
16.390
三、解答题
17.本小题考查三角函数中的诱导公式、特殊角三角函数值、两角差公式、倍角公式、函数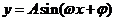 的性质等基础知识,考查基本运算能力.满分12分.
的性质等基础知识,考查基本运算能力.满分12分.
(Ⅰ)解: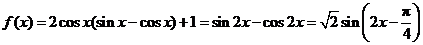 .
.
因此,函数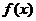 的最小正周期为
的最小正周期为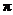 .
.
(Ⅱ)解法一:因为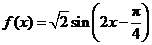 在区间
在区间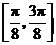 上为增函数,在区间
上为增函数,在区间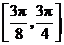 上为减函数,又
上为减函数,又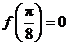 ,
,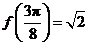 ,
,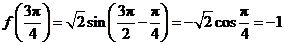 ,
,
故函数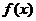 在区间
在区间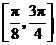 上的最大值为
上的最大值为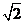 ,最小值为
,最小值为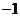 .
.
解法二:作函数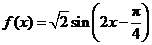 在长度为一个周期的区间
在长度为一个周期的区间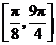 上的图象如下:
上的图象如下:
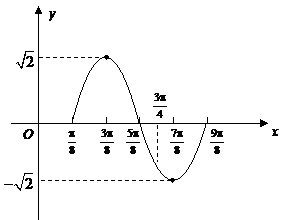
由图象得函数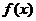 在区间
在区间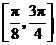 上的最大值为
上的最大值为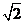 ,最小值为
,最小值为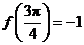 .
.
18.本小题主要考查互斥事件、相互独立事件、离散型随机变量的分布列和数学期望等基础知识,考查运用概率知识解决实际问题的能力.满分12分.
(Ⅰ)解:设“从甲盒内取出的2个球均为黑球”为事件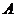 ,“从乙盒内取出的2个球均为黑球”为事件
,“从乙盒内取出的2个球均为黑球”为事件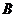 .由于事件
.由于事件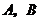 相互独立,且
相互独立,且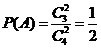 ,
,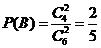 .
.
故取出的4个球均为黑球的概率为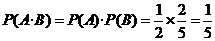 .
.
(Ⅱ)解:设“从甲盒内取出的2个球均为黑球;从乙盒内取出的2个球中,1个是红球,1个是黑球”为事件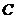 ,“从甲盒内取出的2个球中,1个是红球,1个是黑球;从乙盒内取出的2个球均为黑球”为事件
,“从甲盒内取出的2个球中,1个是红球,1个是黑球;从乙盒内取出的2个球均为黑球”为事件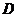 .由于事件
.由于事件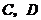 互斥,
互斥,
且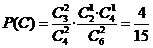 ,
,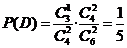 .
.
故取出的4个球中恰有1个红球的概率为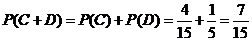 .
.
(Ⅲ)解: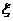 可能的取值为
可能的取值为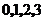 .由(Ⅰ),(Ⅱ)得
.由(Ⅰ),(Ⅱ)得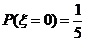 ,
,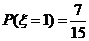 ,
,
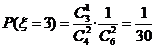 .从而
.从而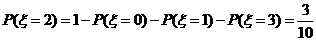 .
.
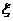 的分布列为
的分布列为
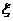 |
0 |
1 |
2 |
3 |
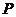 |
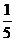 |
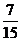 |
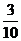 |
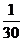 |
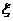 的数学期望
的数学期望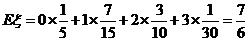 .
.
19.本小题考查直线与直线垂直、直线与平面垂直、二面角等基础知识,考查空间想象能力、运算能力和推理论证能力.满分12分.
(Ⅰ)证明:在四棱锥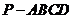 中,因
中,因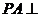 底面
底面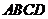 ,
,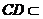 平面
平面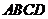 ,故
,故 .
.
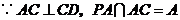 ,
,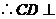 平面
平面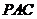 .
.
而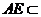 平面
平面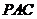 ,
,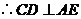 .
.
(Ⅱ)证明:由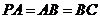 ,
,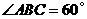 ,可得
,可得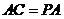 .
.
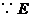 是
是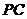 的中点,
的中点,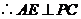 .
.
由(Ⅰ)知,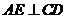 ,且
,且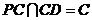 ,所以
,所以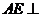 平面
平面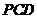 .
.
而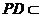 平面
平面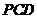 ,
,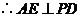 .
.
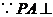 底面
底面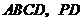 在底面
在底面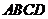 内的射影是
内的射影是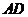 ,
,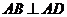 ,
,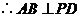 .
.
又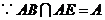 ,综上得
,综上得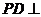 平面
平面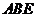 .
.
(Ⅲ)解法一:过点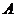 作
作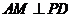 ,垂足为
,垂足为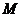 ,连结
,连结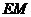 .则(Ⅱ)知,
.则(Ⅱ)知,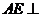 平面
平面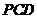 ,
,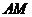 在平面
在平面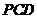 内的射影是
内的射影是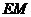 ,则
,则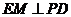 .
.
因此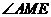 是二面角
是二面角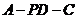 的平面角.
的平面角.
由已知,得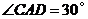 .设
.设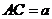 ,
,
可得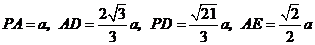 .
.
在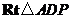 中,
中,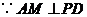 ,
,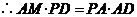 ,
,
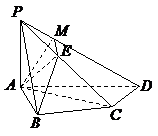 则
则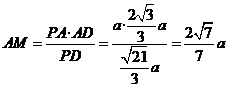 .
.
在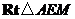 中,
中,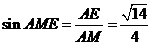 .
.
所以二面角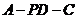 的大小是
的大小是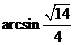 .
.
解法二:由题设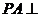 底面
底面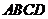 ,
,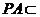 平面
平面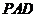 ,则平面
,则平面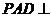 平面
平面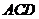 ,交线为
,交线为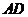 .
.
过点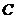 作
作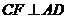 ,垂足为
,垂足为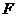 ,故
,故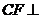 平面
平面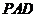 .过点
.过点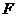 作
作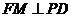 ,垂足为
,垂足为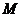 ,连结
,连结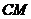 ,故
,故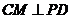 .因此
.因此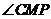 是二面角
是二面角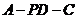 的平面角.
的平面角.
由已知,可得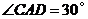 ,设
,设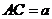 ,
,
可得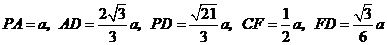 .
.
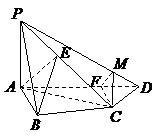
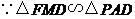 ,
,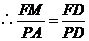 .
.
于是,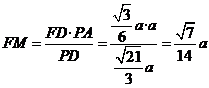 .
.
在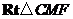 中,
中,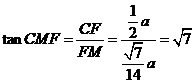 .
.
所以二面角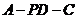 的大小是
的大小是 .
.
20.本小题考查导数的几何意义,两个函数的和、差、积、商的导数,利用导数研究函数的单调性和极值等基础知识,考查运算能力及分类讨论的思想方法.满分12分.
(Ⅰ)解:当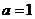 时,
时,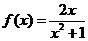 ,
,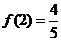 ,
,
又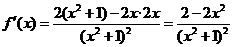 ,
,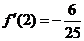 .
.
所以,曲线 在点
在点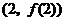 处的切线方程为
处的切线方程为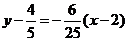 ,
,
即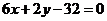 .
.
(Ⅱ)解: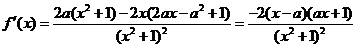 .
.
由于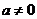 ,以下分两种情况讨论.
,以下分两种情况讨论.
(1)当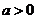 时,令
时,令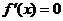 ,得到
,得到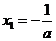 ,
,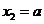 .当
.当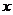 变化时,
变化时,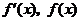 的变化情况如下表:
的变化情况如下表:
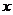 |
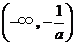 |
 |
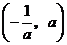 |
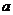 |
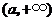 |
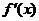 |
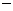 |
0 |
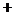 |
0 |
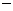 |
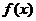 |
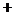 |
极小值 |
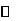 |
极大值 |
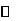 |
所以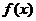 在区间
在区间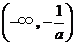 ,
,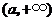 内为减函数,在区间
内为减函数,在区间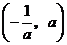 内为增函数.
内为增函数.
函数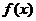 在
在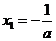 处取得极小值
处取得极小值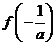 ,且
,且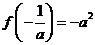 ,
,
函数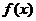 在
在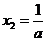 处取得极大值
处取得极大值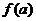 ,且
,且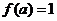 .
.
(2)当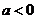 时,令
时,令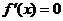 ,得到
,得到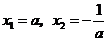 ,当
,当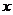 变化时,
变化时,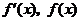 的变化情况如下表:
的变化情况如下表:
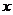 |
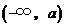 |
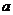 |
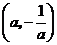 |
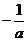 |
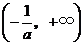 |
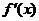 |
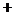 |
0 |
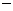 |
0 |
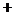 |
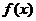 |
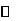 |
极大值 |
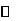 |
极小值 |
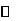 |
所以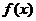 在区间
在区间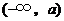 ,
,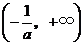 内为增函数,在区间
内为增函数,在区间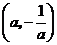 内为减函数.
内为减函数.
函数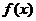 在
在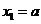 处取得极大值
处取得极大值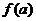 ,且
,且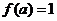 .
.
函数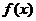 在
在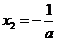 处取得极小值
处取得极小值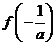 ,且
,且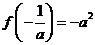 .
.
21.本小题以数列的递推关系式为载体,主要考查等比数列的前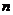 项和公式、数列求和、不等式的证明等基础知识与基本方法,考查归纳、推理、运算及灵活运用数学知识分析问题和解决问题的能力.满分14分.
项和公式、数列求和、不等式的证明等基础知识与基本方法,考查归纳、推理、运算及灵活运用数学知识分析问题和解决问题的能力.满分14分.
(Ⅰ)解法一: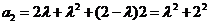 ,
,
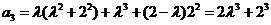 ,
,
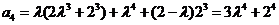 .
.
由此可猜想出数列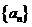 的通项公式为
的通项公式为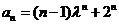 .
.
以下用数学归纳法证明.
(1)当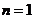 时,
时,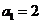 ,等式成立.
,等式成立.
(2)假设当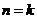 时等式成立,即
时等式成立,即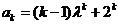 ,
,
那么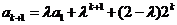
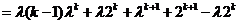
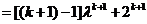 .
.
这就是说,当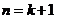 时等式也成立.根据(1)和(2)可知,等式
时等式也成立.根据(1)和(2)可知,等式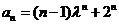 对任何
对任何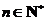 都成立.
都成立.
解法二:由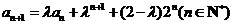 ,
,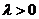 ,
,
可得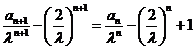 ,
,
所以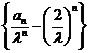 为等差数列,其公差为1,首项为0,故
为等差数列,其公差为1,首项为0,故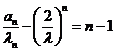 ,所以数列
,所以数列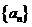 的通项公式为
的通项公式为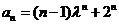 .
.
(Ⅱ)解:设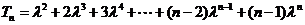 , ①
, ①
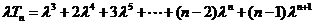 ②
②
当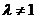 时,①式减去②式,
时,①式减去②式,
得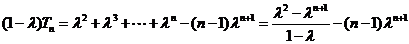 ,
,
 .
.
这时数列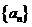 的前
的前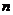 项和
项和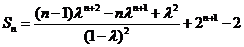 .
.
当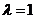 时,
时,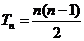 .这时数列
.这时数列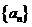 的前
的前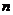 项和
项和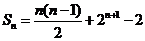 .
.
(Ⅲ)证明:通过分析,推测数列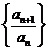 的第一项
的第一项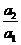 最大,下面证明:
最大,下面证明:
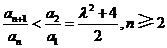 . ③
. ③
由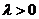 知
知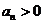 ,要使③式成立,只要
,要使③式成立,只要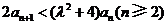 ,
,
因为
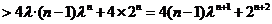
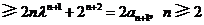 .
.
所以③式成立.
因此,存在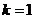 ,使得
,使得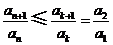 对任意
对任意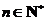 均成立.
均成立.
22.本小题主要考查椭圆的标准方程和几何性质、直线方程、求曲线的方程等基础知识,考查曲线和方程的关系等解析几何的基本思想方法及推理、运算能力.满分14分.
(Ⅰ)证法一:由题设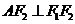 及
及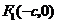 ,
,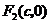 ,不妨设点
,不妨设点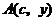 ,其中
,其中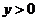 .由于点
.由于点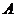 在椭圆上,有
在椭圆上,有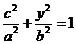 ,即
,即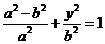 .
.
解得 ,从而得到
,从而得到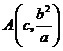 .
.
直线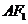 的方程为
的方程为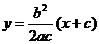 ,整理得
,整理得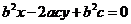 .
.
由题设,原点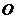 到直线
到直线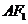 的距离为
的距离为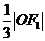 ,即
,即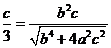 ,
,
将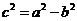 代入上式并化简得
代入上式并化简得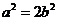 ,即
,即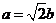 .
.
证法二:同证法一,得到点 的坐标为
的坐标为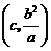 .
.
过点 作
作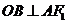 ,垂足为
,垂足为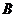 ,易知
,易知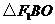
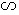
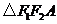 ,故
,故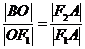 .
.
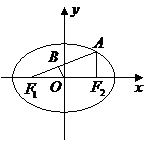 由椭圆定义得
由椭圆定义得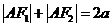 ,又
,又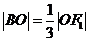 ,
,
所以 ,
,
解得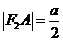 ,而
,而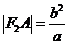 ,得
,得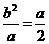 ,即
,即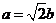 .
.
(Ⅱ)解法一:设点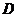 的坐标为
的坐标为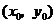 .
.
当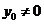 时,由
时,由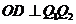 知,直线
知,直线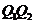 的斜率为
的斜率为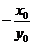 ,所以直线
,所以直线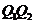 的方程为
的方程为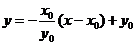 ,或
,或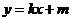 ,其中
,其中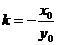 ,
,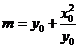 .
.
点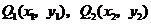 的坐标满足方程组
的坐标满足方程组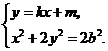
将①式代入②式,得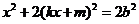 ,
,
整理得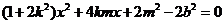 ,
,
于是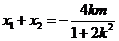 ,
,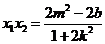 .
.
由①式得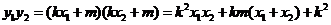
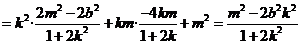 .
.
由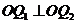 知
知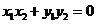 .将③式和④式代入得
.将③式和④式代入得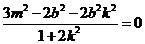 ,
,
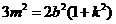 .
.
将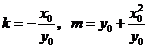 代入上式,整理得
代入上式,整理得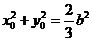 .
.
当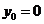 时,直线
时,直线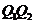 的方程为
的方程为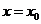 ,
,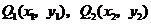 的坐标满足方程组
的坐标满足方程组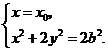
所以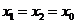 ,
, .
.
由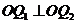 知
知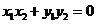 ,即
,即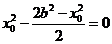 ,
,
解得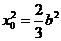 .
.
这时,点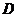 的坐标仍满足
的坐标仍满足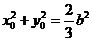 .
.
综上,点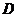 的轨迹方程为
的轨迹方程为 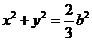 .
.
解法二:设点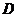 的坐标为
的坐标为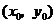 ,直线
,直线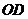 的方程为
的方程为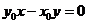 ,由
,由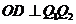 ,垂足为
,垂足为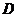 ,可知直线
,可知直线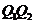 的方程为
的方程为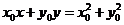 .
.
记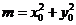 (显然
(显然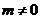 ),点
),点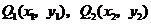 的坐标满足方程组
的坐标满足方程组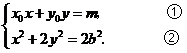
由①式得 . ③
. ③
由②式得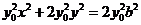 . ④
. ④
将③式代入④式得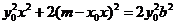 .
.
整理得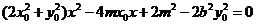 ,
,
于是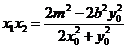 . ⑤
. ⑤
由①式得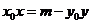 . ⑥
. ⑥
由②式得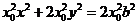 . ⑦
. ⑦
将⑥式代入⑦式得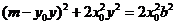 ,
,
整理得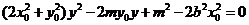 ,
,
于是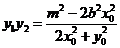 . ⑧
. ⑧
由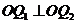 知
知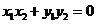 .将⑤式和⑧式代入得
.将⑤式和⑧式代入得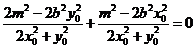 ,
,
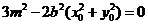 .
.
将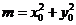 代入上式,得
代入上式,得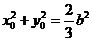 .
.
所以,点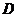 的轨迹方程为
的轨迹方程为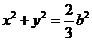 .
.