
网址:http://www.1010jiajiao.com/paper/timu/5157207.html[举报]
12. 同学们都知道,在一次考试后,如果按顺序去掉一些高分,那么班级的平均分将降低;
反之,如果按顺序去掉一些低分,那么班级的平均分将提高. 这两个事实可以用数学语
言描述为:若有限数列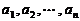 满足
满足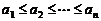 ,则
,则
(结论用数学式子表示).
数 学 试 卷
参考答案及评分标准
一.(第1至12题)每一题正确的给4分,否则一律得零分.
1. 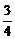 .
2. 2. 3.
.
2. 2. 3. 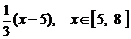 . 4.
. 4. 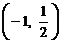 .
.
5. 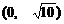 . 6.
. 6.
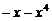 . 7. 48. 8.
. 7. 48. 8. 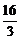 .
.
9. 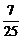 . 10.
2. 11. 4.
. 10.
2. 11. 4.
12. 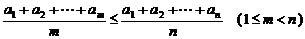 和
和
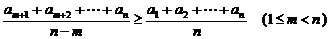
二.(第13至16题)每一题正确的给4分,否则一律得零分.
|
题 号 |
13 |
14 |
15 |
16 |
|
代 号 |
B |
C |
A |
B |
三.(第17至22题)
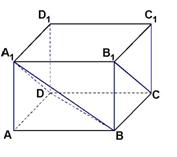
17. [解法一] 连接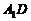 ,
,
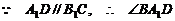 为异面直线
为异面直线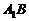 与
与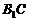 所成的角. ……4分
所成的角. ……4分
连接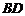 ,在△
,在△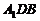 中,
中,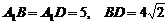 ,
……6分
,
……6分
 则
则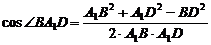
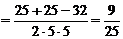 . ……10分
. ……10分
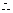 异面直线
异面直线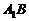 与
与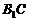 所成角的大小为
所成角的大小为 .
……12分
.
……12分
[解法二] 以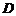 为坐标原点,分别以
为坐标原点,分别以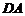 、
、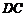 、
、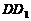 所在直线为
所在直线为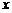 轴、
轴、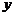 轴、
轴、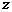 轴,建立空间直角坐标系.
……2分
轴,建立空间直角坐标系.
……2分
则 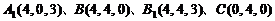 ,
,
 得
得 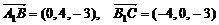 .
……6分
.
……6分
设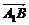 与
与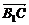 的夹角为
的夹角为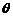 ,
,
则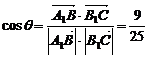 , ……10分
, ……10分
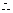
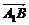 与
与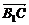 的夹角大小为
的夹角大小为 ,
,
即异面直线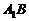 与
与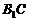 所成角的大小为
所成角的大小为 .
……12分
.
……12分
18. [解法一] 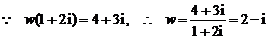 ,
……4分
,
……4分
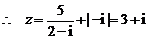 .
……8分
.
……8分
若实系数一元二次方程有虚根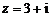 ,则必有共轭虚根
,则必有共轭虚根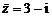 .
.
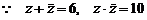 ,
,
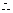 所求的一个一元二次方程可以是
所求的一个一元二次方程可以是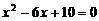 .
……12分
.
……12分
[解法二] 设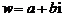
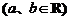
 ,
,
得 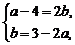
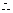
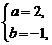
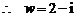 ,
……4分
,
……4分
以下解法同[解法一].
19. [解](1)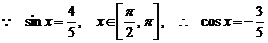 ,
……2分
,
……2分
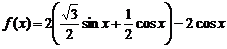 ……4分
……4分
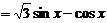
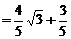 .
……8分
.
……8分
(2)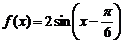 ,
……10分
,
……10分
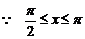 ,
, 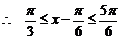 ,
,  ,
,
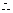 函数
函数 的值域为
的值域为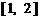 .
……14分
.
……14分
20. [解](1)设曲线方程为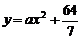 , 由题意可知,
, 由题意可知,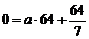 .
.
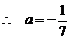 . ……4分
. ……4分
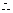 曲线方程为
曲线方程为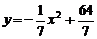 .
……6分
.
……6分
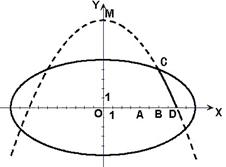 (2)设变轨点为
(2)设变轨点为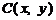 ,根据题意可知
,根据题意可知
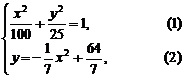 得
得 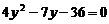 ,
,
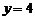 或
或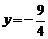 (不合题意,舍去).
(不合题意,舍去).
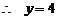 .
……9分
.
……9分
得 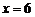 或
或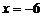 (不合题意,舍去).
(不合题意,舍去). 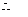
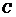 点的坐标为
点的坐标为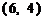 ,
……11分
,
……11分
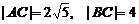 .
.
答:当观测点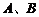 测得
测得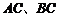 距离分别为
距离分别为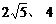 时,应向航天器发出变轨指令.
……14分
时,应向航天器发出变轨指令.
……14分
 21. [解](1)
21. [解](1)
……4分
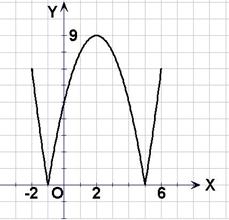
(2)方程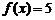 的解分别是
的解分别是 和
和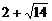 ,由于
,由于 在
在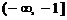 和
和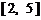 上单调递减,在
上单调递减,在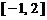 和
和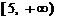 上单调递增,因此
上单调递增,因此
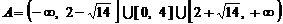 .
……8分
.
……8分
由于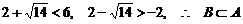 .
……10分
.
……10分
(3)[解法一] 当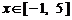 时,
时,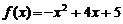 .
.
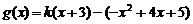
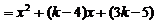
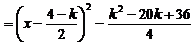 ,
……12分
,
……12分
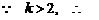
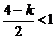 . 又
. 又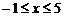 ,
,
① 当 ,即
,即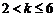 时,取
时,取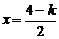 ,
,
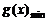
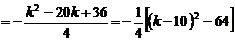 .
.
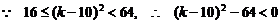 ,
,
则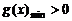 .
……14分
.
……14分
② 当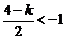 ,即
,即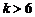 时,取
时,取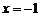 ,
, 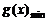 =
=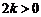 .
.
由 ①、②可知,当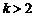 时,
时,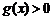 ,
,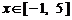 .
.
因此,在区间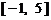 上,
上,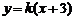 的图像位于函数
的图像位于函数 图像的上方. ……16分
图像的上方. ……16分
[解法二] 当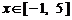 时,
时,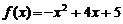 .
.
由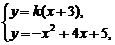 得
得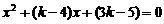 ,
,
令 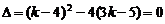 ,解得
,解得
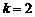 或
或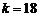 ,
……12分
,
……12分
在区间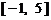 上,当
上,当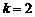 时,
时,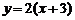 的图像与函数
的图像与函数 的图像只交于一点
的图像只交于一点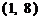 ; 当
; 当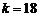 时,
时,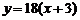 的图像与函数
的图像与函数 的图像没有交点. ……14分
的图像没有交点. ……14分
如图可知,由于直线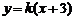 过点
过点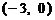 ,当
,当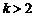 时,直线
时,直线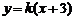 是由直线
是由直线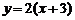 绕点
绕点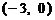 逆时针方向旋转得到. 因此,在区间
逆时针方向旋转得到. 因此,在区间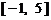 上,
上,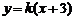 的图像位于函数
的图像位于函数 图像的上方.
……16分
图像的上方.
……16分
22. [解](1)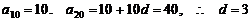 .
…… 4分
.
…… 4分
(2)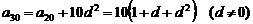 ,
…… 8分
,
…… 8分
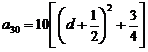 ,
,
当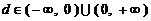 时,
时,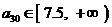 .
…… 12分
.
…… 12分
(3)所给数列可推广为无穷数列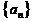 ,其中
,其中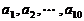 是首项为1,公差为1的等差数列,当
是首项为1,公差为1的等差数列,当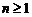 时,数列
时,数列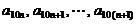 是公差为
是公差为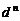 的等差数列.
…… 14分
的等差数列.
…… 14分
研究的问题可以是:试写出 关于
关于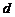 的关系式,并求
的关系式,并求 的取值范围.…… 16分
的取值范围.…… 16分
研究的结论可以是:由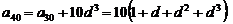 ,
,
依次类推可得 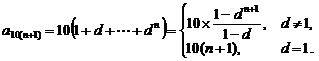
当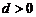 时,
时,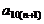 的取值范围为
的取值范围为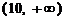 等.
…… 18分
等.
…… 18分