
网址:http://www.1010jiajiao.com/paper/timu/5157219.html[举报]
2.如图,三棱锥P-ABC的高PO = 8,AC = BC = 3,∠ACB = 30°,M、N分别在BC和PO上,且CM = x,PN = 2 cm,则下面四个图象中大致描绘了三棱锥N -AMC的体积V与x ( x∈ )的变化关系的是( )
)的变化关系的是( )


参考答案
1.D 2.A 3.C 4.D 5.(理)C (文)B 6.B 7.(理)C
(文)B 8.D 9.C 10.D 11.C 12.A
13.
14.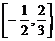
15.(理)10 (文)85
16.8
17.解:把原不等式变为 >0 ,(3分)
>0 ,(3分)
∴当a = 0 ,原不等式的解集为(-∞,0) (6分)
a>0时,原不等式的解集为(-∞,0)∪ (9分)
(9分)
当a<0时,原不等式的解集为( ,0)(12分)
,0)(12分)
18.解:(1)易选择y = A cos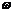 t + B的解析式(2分)
t + B的解析式(2分)
进而求A = 1.5 , 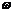 =
=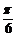 , B
= 1.51。所以函数解析式为:
, B
= 1.51。所以函数解析式为:
y
= 1.5 cos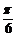 t +1.51 。(8分)
t +1.51 。(8分)
(2)由(1)可知当t = 14时,
y = 1.5 cos (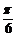 ×14 ) + 1.51 = 1.5×
×14 ) + 1.51 = 1.5× +
1.51 = 2.26 (m)
+
1.51 = 2.26 (m)
所以,午后两点水位高出海平面2.26 m (12分)
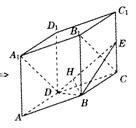 19.(1)
19.(1)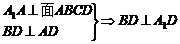 ,
,
又A1D⊥BE,所以A1D⊥面BDE 。(4分)
(2)连接如图所示B1C ,
|
|

EC⊥面ABCD EC⊥BD
EC⊥BD
为二面角E-BD-C的平面角。由△BB1C∽△CBE
可得EC = ,
,
所以tan∠EBC = ,∠EBC = arctan
,∠EBC = arctan (8分)
(8分)
(3)连接DE,作HB垂直DF于H,则易证BH⊥面DA1E,BH的长即为所求。在直角三角形BDE中,易求得BH = 。也可用VB–A1DE = VE
–A1DB 求解。(12分)
。也可用VB–A1DE = VE
–A1DB 求解。(12分)
20.解:(1) = Sn ,( n≥1)
= Sn ,( n≥1)  = Sn–1 (
n≥1 )
= Sn–1 (
n≥1 )
∴ –
– = an , ( n≥2 ) 。(4分)
= an , ( n≥2 ) 。(4分)
整理得:an+1 = ,(n≥2) ,
,(n≥2) ,
an
=  , (3分)
, (3分)
an–1
=
…
a3
=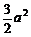
各式相乘得:an =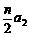 (n≥3)
(n≥3)
由已知可得a2 = 2 , a1 = 1 , 所以an = n , ( n ≥1) (6分)
(2)bn = 2n .n,由错位相减法可得Tn = ( n – 1 ).2n+1 + 2 (12分)
21.解:(理)f′( x
) = 2x +  ,
,
(1)由题意有f′( x )≤0在x∈(0,2)上恒成立。
所以当x∈(0,2)时,2x + ≤0恒成立。
≤0恒成立。
即:x∈(0,2)时,a≤– 2x2∈(-∞,0)
所以a≤– 8(6分)
(2)假设存在与y = 2x平行或重合的切线,则2x + = 2有正根。
= 2有正根。
即:方程a = – 2x2 + 2x = –2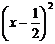 +
+ 有正数解。(8分)
有正数解。(8分)
当a> 时,不存在满足条件的切线;
时,不存在满足条件的切线;
当a = 时,存在一条满足条件的切线;
时,存在一条满足条件的切线;
当0<a< 时,存在两条满足条件的切线;
时,存在两条满足条件的切线;
当a<0时,存在一条满足条件的切线。(12分)
(文)f′( x ) = 3x2 – 2ax – 4 ,
(1)由题意:f′( x )≤0在x∈(0,2)上恒成立。
|
|
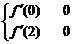 解之得a≥2 (6分)
解之得a≥2 (6分)
(2)假设存在满足条件的a的值,则关于x的一元二次方程
3x2 – 2ax – 4 = –5 有解,即△= 4a2 –12≥0成立,
所以a≥ 或a≤
或a≤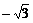 。(12分)
。(12分)
22.解:(1)依题意,可设直线AB的方程为y = kx + m ,代入抛物线方程x2 = 4y得
x2 – 4kx – 4m – 0 ① (2分)
设A,B两点的坐标分别是( x1,y1 ) , ( x2,y2 ),则x1, x2是方程①的两根,所以x1x2 = – 4 m,由点P ( 0 , m ) 分有向线段 所成的比为
所成的比为 ,得
,得 = 0,即
= 0,即 = –
= – ,又点Q是点P关于原点的对称点,故点Q的坐标是 ( 0 , m ) ,从而
,又点Q是点P关于原点的对称点,故点Q的坐标是 ( 0 , m ) ,从而 = ( 0, 2m )。
= ( 0, 2m )。 = (
x1 , y1 + m ) –
= (
x1 , y1 + m ) – ( x2 , y2
+ m ) = ( x1 –
( x2 , y2
+ m ) = ( x1 – x2
, y1 + ( 1 –
x2
, y1 + ( 1 – ) m ) 。
) m ) 。
 = 2m [y1
–
= 2m [y1
– y2 + ( 1 –
y2 + ( 1 – ) m ]
) m ]
= 2m

=2m
( x1 + x2 ). = 0
= 0
所以 。(7分)
。(7分)
(2)由 得点A、B的坐标分别是(–4 ,4)和(6,9)
得点A、B的坐标分别是(–4 ,4)和(6,9)
由x2 = 4y得y =  ,
, 所以折射线x2 = 4y在点A处切线的斜率为y′| x = –
4 = –2 (9分)
所以折射线x2 = 4y在点A处切线的斜率为y′| x = –
4 = –2 (9分)
设圆C的方程是(x – a )2 + ( y – b )2 = r2
则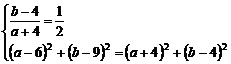
解之得
r2
= ( a + 4 )2 + ( b – 4 )2 =
所以圆C的方程是( x –1 )2
+ 
即x2 + y2 –2x –13y + 12 = 0 (14分)