
网址:http://www.1010jiajiao.com/paper/timu/5157703.html[举报]
27.(全国Ⅰ•理•19题)四棱锥S-ABCD中,底面ABCD为平行四边形,侧面SBC⊥底面ABCD。已知∠ABC=45°,AB=2,BC=2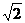 ,SA=SB=
,SA=SB=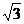 。
。
(Ⅰ)证明:SA⊥BC;
(Ⅱ)求直线SD与平面SAB所成角的大小;
解答:解法一:
(Ⅰ)作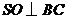 ,垂足为
,垂足为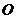 ,连结
,连结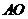 ,由侧面
,由侧面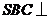 底面
底面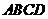 ,得
,得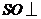 底面
底面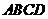 .
.
因为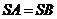 ,所以
,所以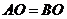 ,
,
又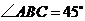 ,故
,故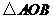 为等腰直角三角形,
为等腰直角三角形, ,
,
由三垂线定理,得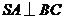 .
.
 (Ⅱ)由(Ⅰ)知
(Ⅱ)由(Ⅰ)知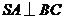 ,依题设
,依题设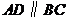 ,
,
故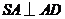 ,由
,由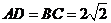 ,
,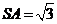 ,
,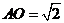 ,得
,得
 ,
,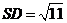 .
.
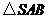 的面积
的面积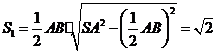 .
.
连结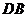 ,得
,得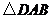 的面积
的面积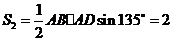
设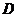 到平面
到平面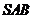 的距离为
的距离为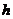 ,由于
,由于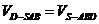 ,得
,得
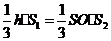 ,
,
解得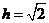 .
.
设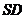 与平面
与平面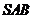 所成角为
所成角为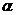 ,则
,则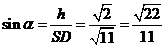 .
.
所以,直线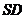 与平面
与平面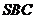 所成的我为
所成的我为 .
.
解法二:
(Ⅰ)作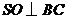 ,垂足为
,垂足为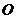 ,连结
,连结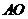 ,由侧面
,由侧面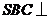 底面
底面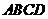 ,得
,得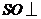 平面
平面 .
.
因为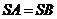 ,所以
,所以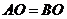 .
.
又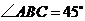 ,
,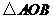 为等腰直角三角形,
为等腰直角三角形, .
.
 如图,以
如图,以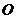 为坐标原点,
为坐标原点,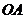 为
为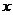 轴正向,建立直角坐标系
轴正向,建立直角坐标系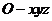 ,
,
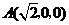 ,
,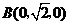 ,
,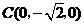 ,
,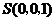 ,
, ,
,
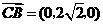 ,
,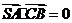 ,所以
,所以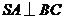 .
.
(Ⅱ)取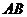 中点
中点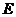 ,
,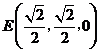 ,
,
连结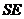 ,取
,取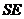 中点
中点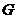 ,连结
,连结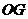 ,
, .
.
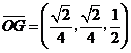 ,
,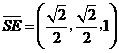 ,
,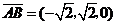 .
.
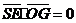 ,
,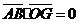 ,
,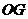 与平面
与平面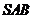 内两条相交直线
内两条相交直线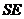 ,
,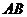 垂直.
垂直.
所以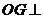 平面
平面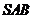 ,
,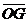 与
与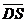 的夹角记为
的夹角记为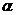 ,
,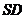 与平面
与平面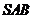 所成的角记为
所成的角记为 ,则
,则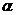 与
与 互余.
互余.
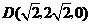 ,
,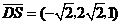 .
.
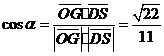 ,
,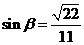 ,
,
所以,直线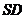 与平面
与平面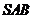 所成的角为
所成的角为 .
.