
网址:http://www.1010jiajiao.com/paper/timu/5157845.html[举报]
5.若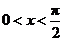 ,则下列命题中正确的是( D )
,则下列命题中正确的是( D )
A.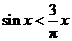 B.
B.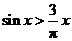
C.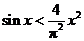 D.
D.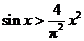
(江西文8)
若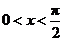 ,则下列命题正确的是( B )
,则下列命题正确的是( B )
A. B.
B.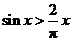 C.
C.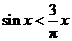 D.
D.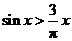
(辽宁理12)
已知 与
与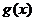 是定义在
是定义在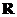 上的连续函数,如果
上的连续函数,如果 与
与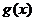 仅当
仅当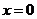 时的函数值为0,且
时的函数值为0,且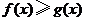 ,那么下列情形不可能出现的是(
)
,那么下列情形不可能出现的是(
)
A.0是 的极大值,也是
的极大值,也是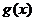 的极大值
的极大值
B.0是 的极小值,也是
的极小值,也是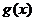 的极小值
的极小值
C.0是 的极大值,但不是
的极大值,但不是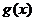 的极值
的极值
D.0是 的极小值,但不是
的极小值,但不是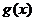 的极值
的极值
(全国一文11)
曲线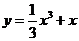 在点
在点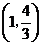 处的切线与坐标轴围成的三角形面积为( A )
处的切线与坐标轴围成的三角形面积为( A )
A.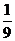 B.
B.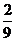 C.
C.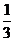 D.
D.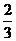
(全国二文8)
已知曲线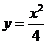 的一条切线的斜率为
的一条切线的斜率为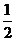 ,则切点的横坐标为( A )
,则切点的横坐标为( A )
A.1 B.2 C.3 D.4
(浙江理8)
设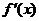 是函数
是函数 的导函数,将
的导函数,将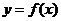 和
和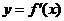 的图象画在同一个直角坐标系中,不可能正确的是( D )
的图象画在同一个直角坐标系中,不可能正确的是( D )
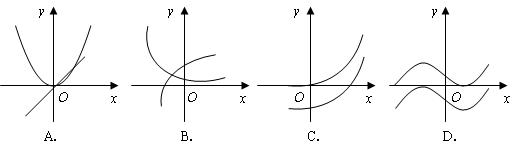
(北京文9)
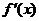 是
是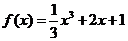 的导函数,则
的导函数,则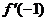 的值是____.3
的值是____.3
(广东文12)
函数 的单调递增区间是____.
的单调递增区间是____.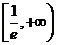
(江苏13)
已知函数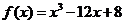 在区间
在区间 上的最大值与最小值分别为
上的最大值与最小值分别为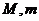 ,则
,则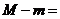 __.32
__.32
(湖北文13)
已知函数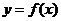 的图象在点
的图象在点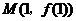 处的切线方程是
处的切线方程是 ,则
,则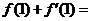 ____.3
____.3
(湖南理13)
函数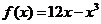 在区间
在区间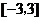 上的最小值是____.
上的最小值是____.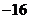
(浙江文15)
曲线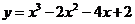 在点
在点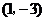 处的切线方程是____.
处的切线方程是____.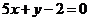
(安徽理 18)
设a≥0,f (x)=x-1-ln2 x+2a ln x(x>0).
(Ⅰ)令F(x)=xf'(x),讨论F(x)在(0.+∞)内的单调性并求极值;
(Ⅱ)求证:当x>1时,恒有x>ln2x-2a ln x+1.
本小题主要考查函数导数的概念与计算,利用导数研究函数的单调性、极值和证明不等式的方法,考查综合运用有关知识解决问题的能力.本小题满分14分.
(Ⅰ)解:根据求导法则有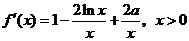 ,
,
故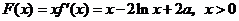 ,
,
于是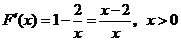 ,
,
列表如下:
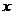 |
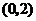 |
2 |
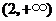 |
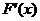 |
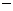 |
0 |
 |
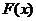 |
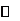 |
极小值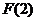 |
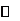 |
故知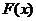 在
在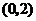 内是减函数,在
内是减函数,在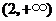 内是增函数,所以,在
内是增函数,所以,在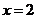 处取得极小值
处取得极小值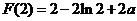 .
.
(Ⅱ)证明:由 知,
知,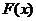 的极小值
的极小值 .
.
于是由上表知,对一切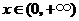 ,恒有
,恒有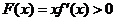 .
.
从而当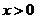 时,恒有
时,恒有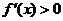 ,故
,故 在
在 内单调增加.
内单调增加.
所以当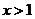 时,
时,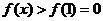 ,即
,即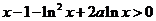 .
.
故当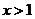 时,恒有
时,恒有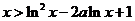 .
.
(安徽文 20)
设函数f(x)=-cos2x-4tsin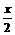 cos
cos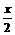 +4t2+t2-3t+4,x∈R,其中
+4t2+t2-3t+4,x∈R,其中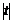 ≤1,将f(x)的最小值记为g(t).
≤1,将f(x)的最小值记为g(t).
(Ⅰ)求g(t)的表达式;
(Ⅱ)诗论g(t)在区间(-1,1)内的单调性并求极值.
本小题主要考查同角三角函数的基本关系,倍角的正弦公式,正弦函数的值域,多项式函数的导数,函数的单调性,考查应用导数分析解决多项式函数的单调区间,极值与最值等问题的综合能力.
解:(I)我们有
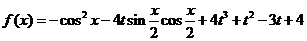
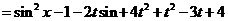
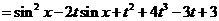
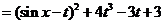 .
.
由于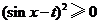 ,
,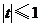 ,故当
,故当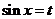 时,
时, 达到其最小值
达到其最小值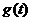 ,即
,即
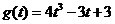 .
.
(II)我们有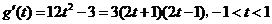 .
.
列表如下:
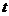 |
 |
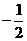 |
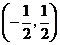 |
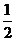 |
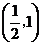 |
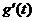 |
 |
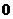 |
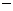 |
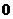 |
 |
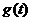 |
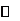 |
极大值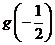 |
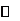 |
极小值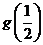 |
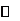 |
由此可见,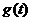 在区间
在区间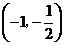 和
和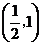 单调增加,在区间
单调增加,在区间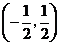 单调减小,极小值为
单调减小,极小值为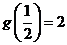 ,极大值为
,极大值为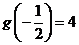 .
.
(北京理 19)
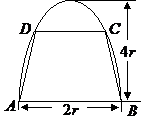 如图,有一块半椭圆形钢板,其半轴长为
如图,有一块半椭圆形钢板,其半轴长为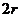 ,短半轴长为
,短半轴长为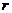 ,计划将此钢板切割成等腰梯形的形状,下底
,计划将此钢板切割成等腰梯形的形状,下底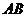 是半椭圆的短轴,上底
是半椭圆的短轴,上底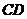 的端点在椭圆上,记
的端点在椭圆上,记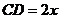 ,梯形面积为
,梯形面积为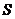 .
.
(I)求面积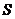 以
以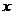 为自变量的函数式,并写出其定义域;
为自变量的函数式,并写出其定义域;
(II)求面积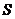 的最大值.
的最大值.
解:(I)依题意,以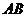 的中点
的中点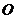 为原点建立直角坐标系
为原点建立直角坐标系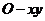 (如图),则点
(如图),则点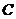 的横坐标为
的横坐标为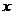 .
.
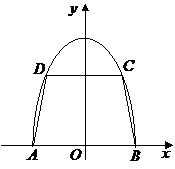 点
点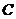 的纵坐标
的纵坐标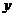 满足方程
满足方程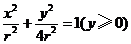 ,
,
解得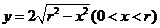
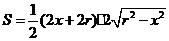
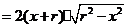 ,
,
其定义域为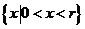 .
.
(II)记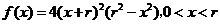 ,
,
则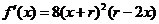 .
.
令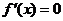 ,得
,得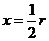 .
.
因为当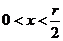 时,
时,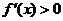 ;当
;当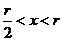 时,
时,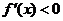 ,所以
,所以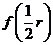 是
是 的最大值.
的最大值.
因此,当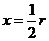 时,
时,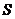 也取得最大值,最大值为
也取得最大值,最大值为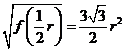 .
.
即梯形面积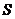 的最大值为
的最大值为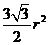 .
.
(福建理 22)
已知函数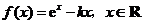
(Ⅰ)若 ,试确定函数
,试确定函数 的单调区间;
的单调区间;
(Ⅱ)若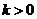 ,且对于任意
,且对于任意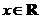 ,
,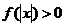 恒成立,试确定实数
恒成立,试确定实数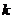 的取值范围;
的取值范围;
(Ⅲ)设函数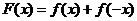 ,求证:
,求证: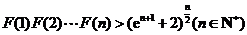 .
.
本小题主要考查函数的单调性、极值、导数、不等式等基本知识,考查运用导数研究函数性质的方法,考查分类讨论、化归以及数形结合等数学思想方法,考查分析问题、解决问题的能力.满分14分.
解:(Ⅰ)由 得
得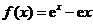 ,所以
,所以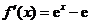 .
.
由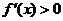 得
得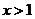 ,故
,故 的单调递增区间是
的单调递增区间是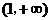 ,
,
由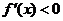 得
得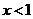 ,故
,故 的单调递减区间是
的单调递减区间是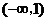 .
.
(Ⅱ)由 可知
可知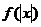 是偶函数.
是偶函数.
于是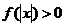 对任意
对任意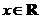 成立等价于
成立等价于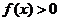 对任意
对任意 成立.
成立.
由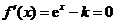 得
得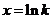 .
.
①当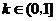 时,
时,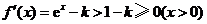 .
.
此时 在
在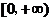 上单调递增.
上单调递增.
故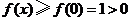 ,符合题意.
,符合题意.
②当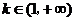 时,
时,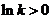 .
.
当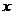 变化时
变化时 的变化情况如下表:
的变化情况如下表:
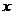 |
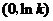 |
 |
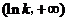 |
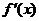 |
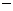 |
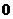 |
 |
 |
单调递减 |
极小值 |
单调递增 |
由此可得,在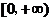 上,
上,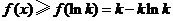 .
.
依题意, ,又
,又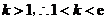 .
.
综合①,②得,实数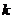 的取值范围是
的取值范围是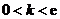 .
.
(Ⅲ)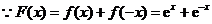 ,
,
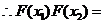
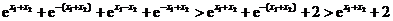 ,
,
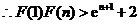 ,
,
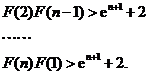
由此得,
故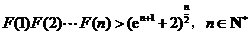 .
.
(福建文 20)
设函数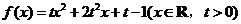 .
.
(Ⅰ)求 的最小值
的最小值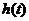 ;
;
(Ⅱ)若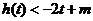 对
对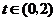 恒成立,求实数
恒成立,求实数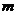 的取值范围.
的取值范围.
本题主要考查函数的单调性、极值以及函数导数的应用,考查运用数学知识分析问题解决问题的能力.满分12分.
解:(Ⅰ)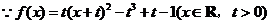 ,
,
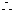 当
当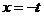 时,
时, 取最小值
取最小值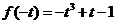 ,
,
即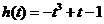 .
.
(Ⅱ)令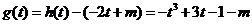 ,
,
由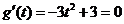 得
得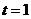 ,
,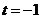 (不合题意,舍去).
(不合题意,舍去).
当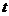 变化时
变化时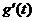 ,
,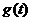 的变化情况如下表:
的变化情况如下表:
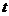 |
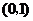 |
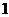 |
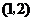 |
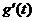 |
 |
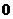 |
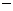 |
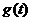 |
递增 |
极大值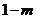 |
递减 |
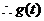 在
在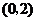 内有最大值
内有最大值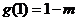 .
.
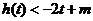 在
在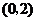 内恒成立等价于
内恒成立等价于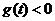 在
在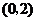 内恒成立,
内恒成立,
即等价于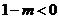 ,
,
所以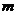 的取值范围为
的取值范围为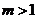 .
.
(广东理、文 20)
已知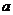 是实数,函数
是实数,函数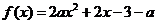 .如果函数
.如果函数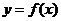 在区间
在区间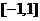 上有
上有
零点,求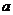 的取值范围.
的取值范围.
解: 若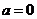 ,
,
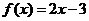 ,显然在上没有零点, 所以
,显然在上没有零点, 所以 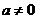
令 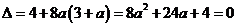 得
得 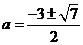
当 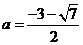 时,
时, 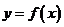 恰有一个零点在
恰有一个零点在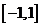 上;
上;
当  即
即 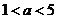 时,
时, 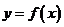 也恰有一个零点在
也恰有一个零点在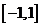 上;
上;
当 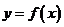 在
在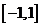 上有两个零点时, 则
上有两个零点时, 则
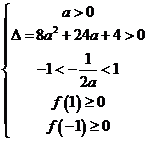 或
或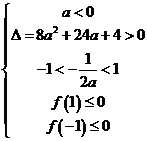
解得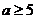 或
或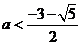
因此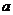 的取值范围是
的取值范围是 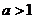 或
或 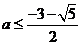 ;
;
(海南理 21)
设函数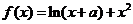
(I)若当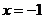 时,
时, 取得极值,求
取得极值,求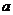 的值,并讨论
的值,并讨论 的单调性;
的单调性;
(II)若 存在极值,求
存在极值,求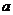 的取值范围,并证明所有极值之和大于
的取值范围,并证明所有极值之和大于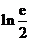 .
.
解:(Ⅰ)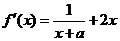 ,
,
依题意有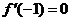 ,故
,故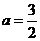 .
.
从而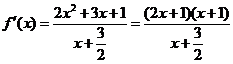 .
.
 的定义域为
的定义域为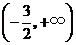 ,当
,当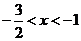 时,
时,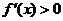 ;
;
当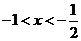 时,
时,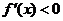 ;
;
当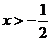 时,
时,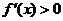 .
.
从而, 分别在区间
分别在区间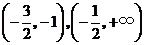 单调增加,在区间
单调增加,在区间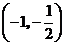 单调减少.
单调减少.
(Ⅱ) 的定义域为
的定义域为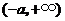 ,
,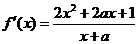 .
.
方程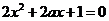 的判别式
的判别式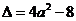 .
.
(ⅰ)若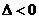 ,即
,即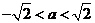 ,在
,在 的定义域内
的定义域内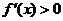 ,故
,故 的极值.
的极值.
(ⅱ)若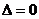 ,则
,则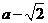 或
或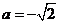 .
.
若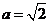 ,
,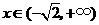 ,
, .
.
当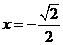 时,
时,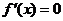 ,当
,当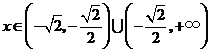 时,
时,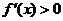 ,所以
,所以 无极值.
无极值.
若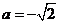 ,
,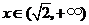 ,
,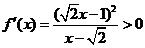 ,
, 也无极值.
也无极值.
(ⅲ)若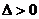 ,即
,即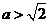 或
或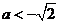 ,则
,则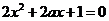 有两个不同的实根
有两个不同的实根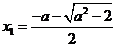 ,
,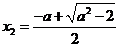 .
.
当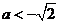 时,
时,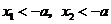 ,从而
,从而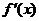 有
有 的定义域内没有零点,故
的定义域内没有零点,故 无极值.
无极值.
当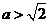 时,
时,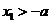 ,
,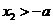 ,
,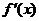 在
在 的定义域内有两个不同的零点,由根值判别方法知
的定义域内有两个不同的零点,由根值判别方法知 在
在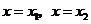 取得极值.
取得极值.
综上, 存在极值时,
存在极值时,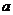 的取值范围为
的取值范围为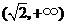 .
.
 的极值之和为
的极值之和为
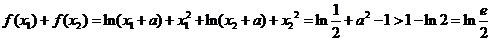 .
.
(海南文 19)
设函数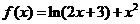
(Ⅰ)讨论 的单调性;
的单调性;
(Ⅱ)求 在区间
在区间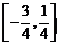 的最大值和最小值.
的最大值和最小值.
解: 的定义域为
的定义域为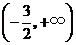 .
.
(Ⅰ)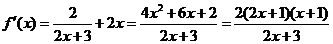 .
.
当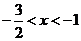 时,
时,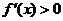 ;当
;当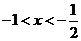 时,
时,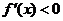 ;当
;当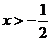 时,
时,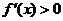 .
.
从而, 分别在区间
分别在区间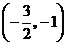 ,
,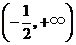 单调增加,在区间
单调增加,在区间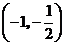 单调减少.
单调减少.
(Ⅱ)由(Ⅰ)知 在区间
在区间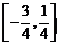 的最小值为
的最小值为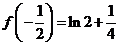 .
.
又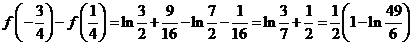
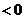 .
.
所以 在区间
在区间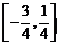 的最大值为
的最大值为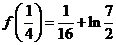 .
.
(湖北理 20)
已知定义在正实数集上的函数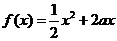 ,
,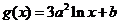 ,其中
,其中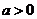 .设两曲线
.设两曲线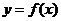 ,
,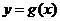 有公共点,且在该点处的切线相同.
有公共点,且在该点处的切线相同.
(I)用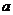 表示
表示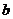 ,并求
,并求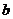 的最大值;
的最大值;
(II)求证: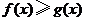 (
(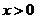 ).
).
本小题主要考查函数、不等式和导数的应用等知识,考查综合运用数学知识解决问题的能力.
解:(Ⅰ)设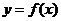 与
与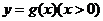 在公共点
在公共点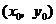 处的切线相同.
处的切线相同.
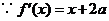 ,
,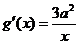 ,由题意
,由题意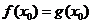 ,
,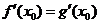 .
.
即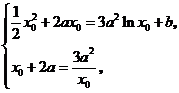 由
由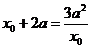 得:
得: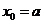 ,或
,或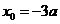 (舍去).
(舍去).
即有 .
.
令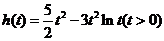 ,则
,则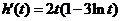 .于是
.于是
当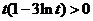 ,即
,即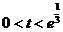 时,
时,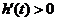 ;
;
当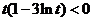 ,即
,即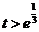 时,
时,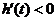 .
.
故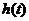 在
在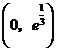 为增函数,在
为增函数,在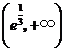 为减函数,
为减函数,
于是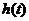 在
在 的最大值为
的最大值为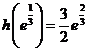 .
.
(Ⅱ)设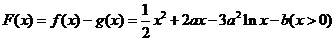 ,
,
则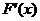
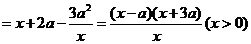 .
.
故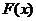 在
在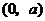 为减函数,在
为减函数,在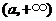 为增函数,
为增函数,
于是函数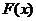 在
在 上的最小值是
上的最小值是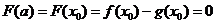 .
.
故当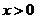 时,有
时,有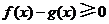 ,即当
,即当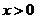 时,
时,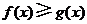 .
.
(湖北文 19)
设二次函数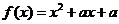 ,方程
,方程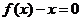 的两根
的两根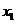 和
和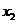 满足
满足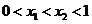 .
.
(I)求实数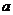 的取值范围;
的取值范围;
(II)试比较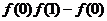 与
与 的大小.并说明理由.
的大小.并说明理由.
本小题主要考查二次函数、二次方程的基本性质及二次不等式的解法,考查推理和运算能力.
解法1:(Ⅰ)令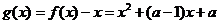 ,
,
则由题意可得
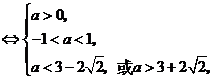
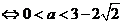 .
.
故所求实数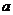 的取值范围是
的取值范围是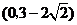 .
.
(II)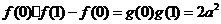 ,令
,令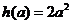 .
.
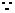 当
当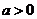 时,
时,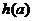 单调增加,
单调增加,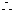 当
当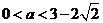 时,
时,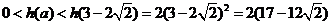
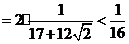 ,即
,即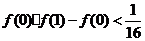 .
.
解法2:(I)同解法1.
(II)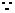
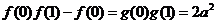 ,由(I)知
,由(I)知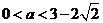 ,
,
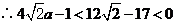 .又
.又 于是
于是
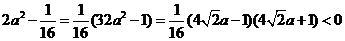 ,
,
即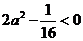 ,故
,故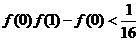 .
.
解法3:(I)方程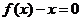
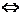
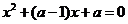 ,由韦达定理得
,由韦达定理得
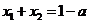 ,
,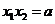 ,于是
,于是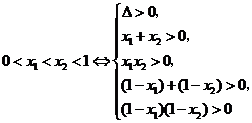
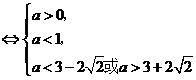
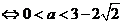 .
.
故所求实数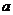 的取值范围是
的取值范围是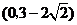 .
.
(II)依题意可设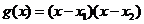 ,则由
,则由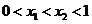 ,得
,得
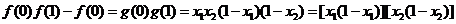
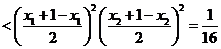 ,故
,故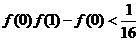 .
.
(湖南理 19)
如图4,某地为了开发旅游资源,欲修建一条连接风景点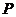 和居民区
和居民区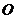 的公路,点
的公路,点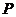 所在的山坡面与山脚所在水平面
所在的山坡面与山脚所在水平面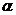 所成的二面角为
所成的二面角为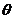 (
(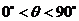 ),且
),且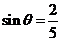 ,点
,点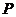 到平面
到平面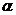 的距离
的距离 (km).沿山脚原有一段笔直的公路
(km).沿山脚原有一段笔直的公路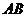 可供利用.从点
可供利用.从点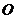 到山脚修路的造价为
到山脚修路的造价为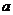 万元/km,原有公路改建费用为
万元/km,原有公路改建费用为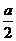 万元/km.当山坡上公路长度为
万元/km.当山坡上公路长度为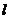 km(
km(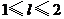 )时,其造价为
)时,其造价为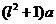 万元.已知
万元.已知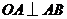 ,
,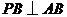 ,
,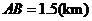 ,
,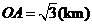 .
.
(I)在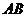 上求一点
上求一点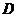 ,使沿折线
,使沿折线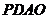 修建公路的总造价最小;
修建公路的总造价最小;
(II) 对于(I)中得到的点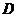 ,在
,在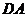 上求一点
上求一点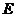 ,使沿折线
,使沿折线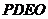 修建公路的总造价最小.
修建公路的总造价最小.
(III)在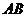 上是否存在两个不同的点
上是否存在两个不同的点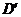 ,
,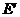 ,使沿折线
,使沿折线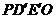 修建公路的总造价小于(II)中得到的最小总造价,证明你的结论.
修建公路的总造价小于(II)中得到的最小总造价,证明你的结论.
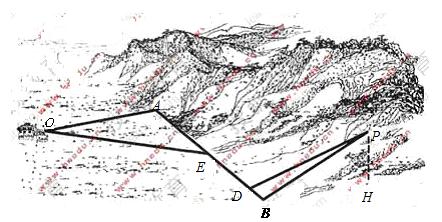
解:(I)如图,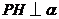 ,
,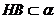 ,
,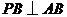 ,
,
由三垂线定理逆定理知,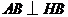 ,所以
,所以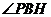 是
是
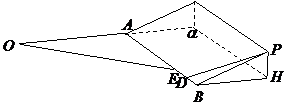 山坡与
山坡与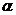 所成二面角的平面角,则
所成二面角的平面角,则 ,
,
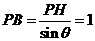 .
.
设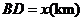 ,
,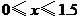 .则
.则
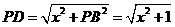
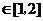 .
.
记总造价为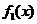 万元,
万元,
据题设有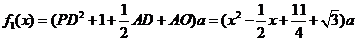
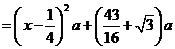
当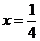 ,即
,即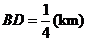 时,总造价
时,总造价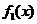 最小.
最小.
(II)设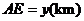 ,
,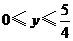 ,总造价为
,总造价为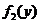 万元,根据题设有
万元,根据题设有
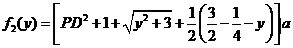
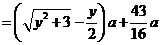 .
.
则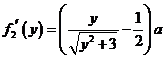 ,由
,由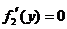 ,得
,得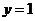 .
.
当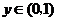 时,
时,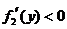 ,
,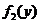 在
在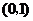 内是减函数;
内是减函数;
当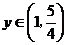 时,
时,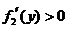 ,
,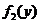 在
在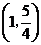 内是增函数.
内是增函数.
故当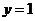 ,即
,即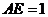 (km)时总造价
(km)时总造价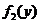 最小,且最小总造价为
最小,且最小总造价为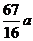 万元.
万元.
(III)解法一:不存在这样的点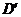 ,
,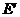 .
.
事实上,在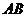 上任取不同的两点
上任取不同的两点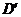 ,
,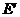 .为使总造价最小,
.为使总造价最小,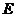 显然不能位于
显然不能位于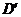 与
与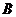 之间.故可设
之间.故可设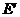 位于
位于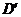 与
与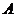 之间,且
之间,且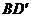 =
= ,
,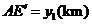 ,
,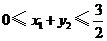 ,总造价为
,总造价为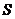 万元,则
万元,则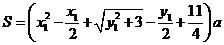 .类似于(I)、(II)讨论知,
.类似于(I)、(II)讨论知,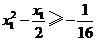 ,
,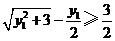 ,当且仅当
,当且仅当 ,
,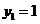 同时成立时,上述两个不等式等号同时成立,此时
同时成立时,上述两个不等式等号同时成立,此时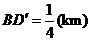 ,
,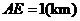 ,
,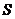 取得最小值
取得最小值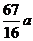 ,点
,点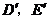 分别与点
分别与点 重合,所以不存在这样的点
重合,所以不存在这样的点 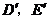 ,使沿折线
,使沿折线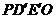 修建公路的总造价小于(II)中得到的最小总造价.
修建公路的总造价小于(II)中得到的最小总造价.
解法二:同解法一得
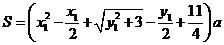
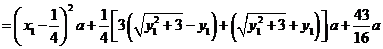
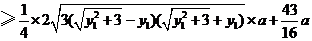
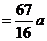 .
.
当且仅当 且
且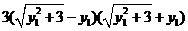 ,即
,即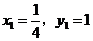 同时成立时,
同时成立时,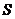 取得最小值
取得最小值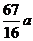 ,以上同解法一.
,以上同解法一.
(湖南文 21)
已知函数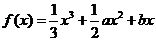 在区间
在区间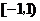 ,
,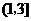 内各有一个极值点.
内各有一个极值点.
(I)求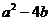 的最大值;
的最大值;
(II)当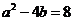 时,设函数
时,设函数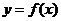 在点
在点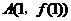 处的切线为
处的切线为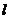 ,若
,若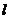 在点
在点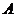 处穿过函数
处穿过函数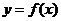 的图象(即动点在点
的图象(即动点在点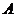 附近沿曲线
附近沿曲线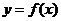 运动,经过点
运动,经过点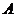 时,从
时,从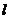 的一侧进入另一侧),求函数
的一侧进入另一侧),求函数 的表达式.
的表达式.
解:(I)因为函数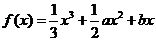 在区间
在区间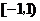 ,
,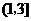 内分别有一个极值点,所以
内分别有一个极值点,所以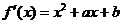
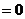 在
在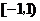 ,
,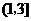 内分别有一个实根,
内分别有一个实根,
设两实根为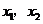 (
( ),则
),则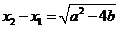 ,且
,且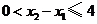 .于是
.于是
 ,
,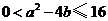 ,且当
,且当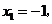
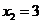 ,即
,即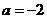 ,
,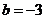 时等号成立.故
时等号成立.故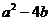 的最大值是16.
的最大值是16.
(II)解法一:由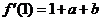 知
知 在点
在点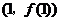 处的切线
处的切线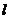 的方程是
的方程是
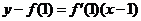 ,即
,即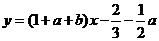 ,
,
因为切线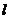 在点
在点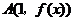 处空过
处空过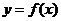 的图象,
的图象,
所以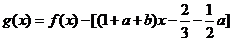 在
在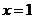 两边附近的函数值异号,则
两边附近的函数值异号,则
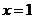 不是
不是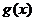 的极值点.
的极值点.
而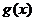
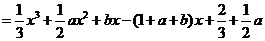 ,且
,且
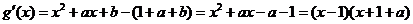 .
.
若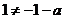 ,则
,则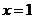 和
和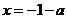 都是
都是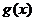 的极值点.
的极值点.
所以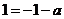 ,即
,即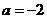 ,又由
,又由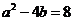 ,得
,得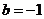 ,故
,故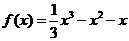 .
.
解法二:同解法一得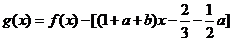
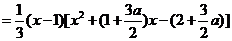 .
.
因为切线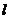 在点
在点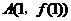 处穿过
处穿过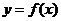 的图象,所以
的图象,所以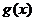 在
在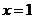 两边附近的函数值异号,于是存在
两边附近的函数值异号,于是存在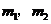 (
(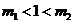 ).
).
当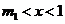 时,
时, ,当
,当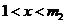 时,
时,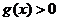 ;
;
或当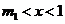 时,
时,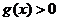 ,当
,当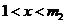 时,
时, .
.
设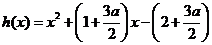 ,则
,则
当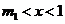 时,
时,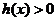 ,当
,当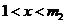 时,
时,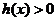 ;
;
或当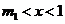 时,
时,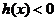 ,当
,当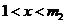 时,
时,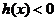 .
.
由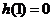 知
知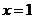 是
是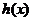 的一个极值点,则
的一个极值点,则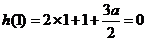 ,
,
所以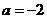 ,又由
,又由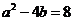 ,得
,得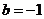 ,故
,故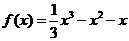 .
.
(辽宁理 22)
已知函数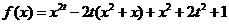 ,
,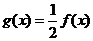 .
.
(I)证明:当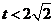 时,
时,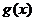 在
在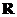 上是增函数;
上是增函数;
(II)对于给定的闭区间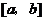 ,试说明存在实数
,试说明存在实数 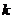 ,当
,当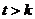 时,
时,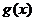 在闭区间
在闭区间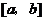 上是减函数;
上是减函数;
(III)证明: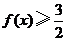 .
.
(辽宁文 22)
已知函数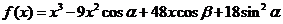 ,
,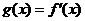 ,且对任意的实数
,且对任意的实数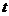 均有
均有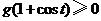 ,
,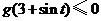 .
.
(I)求函数 的解析式;
的解析式;
(II)若对任意的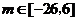 ,恒有
,恒有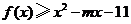 ,求
,求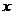 的取值范围.
的取值范围.
(全国一 理20)
设函数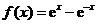 .
.
(Ⅰ)证明: 的导数
的导数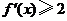 ;
;
(Ⅱ)若对所有 都有
都有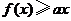 ,求
,求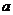 的取值范围.
的取值范围.
解:(Ⅰ) 的导数
的导数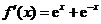 .
.
由于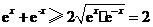 ,故
,故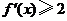 .
.
(当且仅当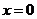 时,等号成立).
时,等号成立).
(Ⅱ)令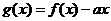 ,则
,则
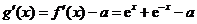 ,
,
(ⅰ)若 ,当
,当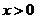 时,
时,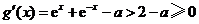 ,
,
故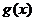 在
在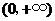 上为增函数,
上为增函数,
所以, 时,
时, ,即
,即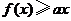 .
.
(ⅱ)若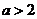 ,方程
,方程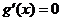 的正根为
的正根为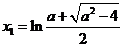 ,
,
此时,若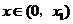 ,则
,则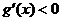 ,故
,故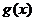 在该区间为减函数.
在该区间为减函数.
所以,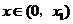 时,
时,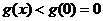 ,即
,即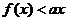 ,与题设
,与题设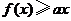 相矛盾.
相矛盾.
综上,满足条件的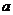 的取值范围是
的取值范围是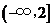 .
.
(全国一文 20)
设函数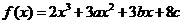 在
在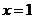 及
及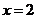 时取得极值
时取得极值