
网址:http://www.1010jiajiao.com/paper/timu/5157863.html[举报]
1.人教A版选修2-2第96页例1 在ΔABC中,三个内角A,B,C对应的边分别为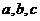 ,且A,B,C成等差数列,
,且A,B,C成等差数列,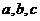 成等比数列,求证ΔABC为等边三角形.
成等比数列,求证ΔABC为等边三角形.
变式1:在ΔABC中,三个内角A,B,C对应的边分别为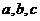 ,且A,B,C成等差数列,
,且A,B,C成等差数列,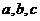 也成等差数列,求证ΔABC为等边三角形.
也成等差数列,求证ΔABC为等边三角形.
证明:由A,B,C成等差数列知,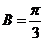 ,由余弦定理知
,由余弦定理知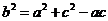 ,
,
又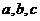 也成等差数列,∴
也成等差数列,∴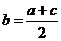 ,代入上式得
,代入上式得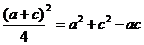 ,
,
整理得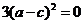 ,∴
,∴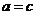 ,从而
,从而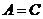 ,而
,而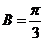 ,则
,则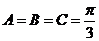 ,
,
从而ΔABC为等边三角形.
变式2:在ΔABC中,三个内角A,B,C对应的边分别为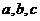 ,且
,且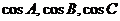 成等比数列,
成等比数列,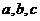 成等差数列,求证ΔABC为等边三角形.
成等差数列,求证ΔABC为等边三角形.
证明:由于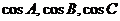 成等比数列,则
成等比数列,则 ,即
,即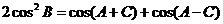 ∴
∴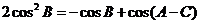 (1)
(1)
又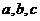 成等差数列,则
成等差数列,则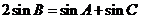
则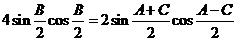 ,
,
由于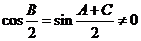 ,∴
,∴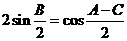 ,即
,即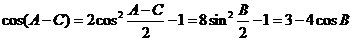 (2)
(2)
将(2)式代入(1)式得: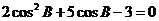 ,
,
∴ 或
或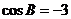 (舍去),而
(舍去),而 ,∴
,∴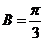 (3)
(3)
将(3)代入(1)得: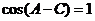 ,由于
,由于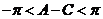 ,∴
,∴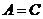 ,
,
因此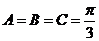 ,从而ΔABC为等边三角形.
,从而ΔABC为等边三角形.
变式3:在ΔABC中,三个内角A,B,C对应的边分别为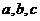 ,且
,且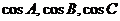 成等比数列,
成等比数列,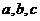 成等比数列,求证ΔABC为等边三角形.
成等比数列,求证ΔABC为等边三角形.
证明:由于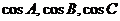 成等比数列,则
成等比数列,则 ,即
,即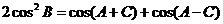 ∴
∴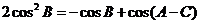 (1)
(1)
又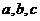 成等比数列,则
成等比数列,则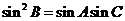 ,∴
,∴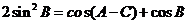 ,
,
即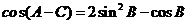 (2)
(2)
将(2)代入(1)得: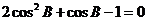 ,∴
,∴ 或
或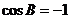 (舍去)
(舍去)
而 ,∴
,∴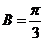 (3)将(3)代入(1)得:
(3)将(3)代入(1)得: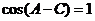 ,
,
由于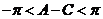 ,∴
,∴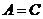 ,因此
,因此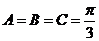 ,从而ΔABC为等边三角形.
,从而ΔABC为等边三角形.
变式4:在ΔABC中,三个内角A,B,C对应的边分别为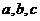 ,且
,且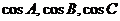 成等差数列,
成等差数列,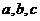 成等差数列,求证ΔABC为等边三角形.
成等差数列,求证ΔABC为等边三角形.
证明:由于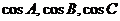 成等差数列,则
成等差数列,则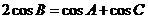 =
=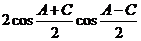
∴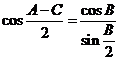 (1)
(1)
又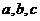 成等差数列,则
成等差数列,则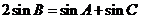 ,∴
,∴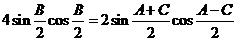 ,
,
由于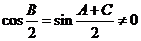 ,∴
,∴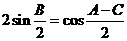 (2)
(2)
将(1)代入(2)得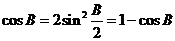 ,∴
,∴ ,而
,而 ,∴
,∴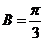 (3)将(3)代入(2)得:
(3)将(3)代入(2)得: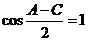 ,由于
,由于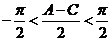 ,∴
,∴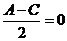 ,
,
因此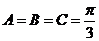 ,从而ΔABC为等边三角形.
,从而ΔABC为等边三角形.
变式5: 在ΔABC中,三个内角A,B,C对应的边分别为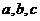 ,且
,且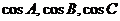 成等差数列,
成等差数列,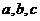 成等比数列,求证ΔABC为等边三角形.
成等比数列,求证ΔABC为等边三角形.
证明:由于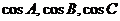 成等差数列,则
成等差数列,则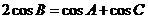 =
=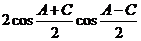
∴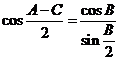 ,则
,则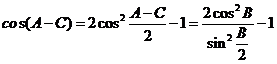 (1)
(1)
又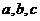 成等比数列,则
成等比数列,则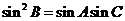 ,∴
,∴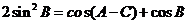 ,
,
即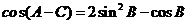 (2)
(2)
将(1)代入(2)整理得: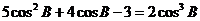
即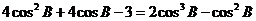 ,分解因式得
,分解因式得
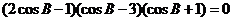 ,∴
,∴ 或
或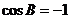 (舍去)或
(舍去)或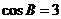 (舍去)
(舍去)
而 ,∴
,∴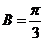 (3)将(3)代入(2)得:
(3)将(3)代入(2)得: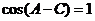 ,
,
由于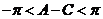 ,∴
,∴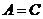 ,因此
,因此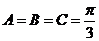 ,从而ΔABC为等边三角形.
,从而ΔABC为等边三角形.