
网址:http://www.1010jiajiao.com/paper/timu/5157884.html[举报]
20.(本小题满分12分)
已知圆C圆心在x轴,且过两点A(-1,1),B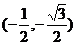
(1)求圆C的方程
(2)设有点列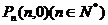 ,过点Pn(n=1,2……)引圆C的切线,若切线的斜率为kn,求和
,过点Pn(n=1,2……)引圆C的切线,若切线的斜率为kn,求和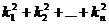
参考答案
一、选择题(每小题5分,共60分):
|
二、填空题(每小题4分,共16分):
13.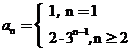 ; 14.
; 14.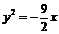 或
或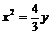 ; 15.
; 15. 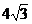 ; 16.①⑤.
; 16.①⑤.
三、解答题:
17.(12分) 解(1):设直线 的方程为:
的方程为: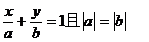 ……2分,
……2分,
又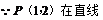
 上,
上,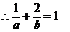 ……3分
……3分
由①②解得a=3,b=3或a=-1,b=1 ……5分
∴直线 的方程为:x+y-3=0或x-y+1=0
……6分
的方程为:x+y-3=0或x-y+1=0
……6分
(2)因为(1)中所求得的两条直线互相垂直,所以y轴被两直线截得的线段即是所求圆的直径且经过P点.令圆心为(0,b),
又x+y-3=0和x-y+1=0在y轴截距分别为3和1, ……9分
则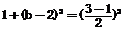 =r2
, 得到b=2.
……11分
=r2
, 得到b=2.
……11分
所求圆的标准方程为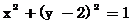 .
……12分
.
……12分
18.(12分)(1)解: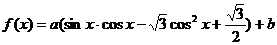
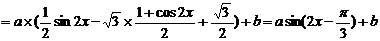 .……4分
∵a>0,x∈R,∴f
(x)的递减区间是
.……4分
∵a>0,x∈R,∴f
(x)的递减区间是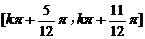 (k∈Z)……6分
(k∈Z)……6分
(2)解:∵x∈[0, ],∴2x∈[0,
],∴2x∈[0,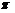 ],2x-
],2x-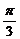 ∈[
∈[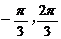 ] …….8分
∴
] …….8分
∴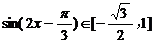 ……9分 ∴函数f (x)的
……9分 ∴函数f (x)的
最小值是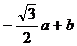 ,最大值是
,最大值是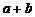
由已知得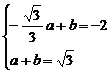 ,……11分. 解得a=2,b=
,……11分. 解得a=2,b=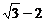 ……12分
……12分
19. (12分)解法一:(Ⅰ)取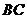 中点
中点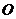 ,连结
,连结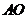 .
.
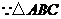 为正三角形,
为正三角形,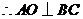 .
.
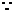 正三棱柱
正三棱柱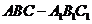 中,平面
中,平面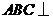 平面
平面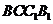 ,
,
 平面
平面 .
.
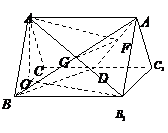 连结
连结 ,在正方形
,在正方形 中,
中,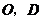 分别为
分别为 的中点,
的中点,
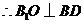 ,
,
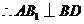 .在正方形
.在正方形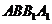 中,
中,
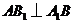 ,
,
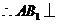 平面
平面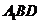 .
.
(Ⅱ)设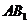 与
与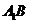 交于点
交于点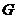 ,在平面
,在平面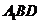 中,
中,
作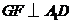 于
于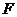 ,连结
,连结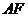 ,
,
由(Ⅰ)得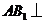 平面
平面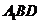 .
.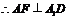 ,
,
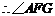 为二面角
为二面角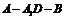 的平面角.
的平面角.
在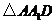 中,由等面积法可求得
中,由等面积法可求得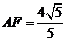 ,
,
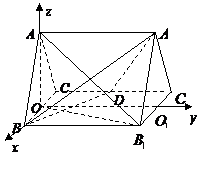 又
又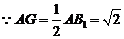 ,
,
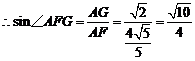 .
.
所以二面角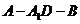 的大小为
的大小为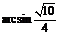 .
.
解法二:(Ⅰ)取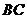 中点
中点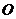 ,连结
,连结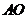 .
.
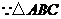 为正三角形,
为正三角形,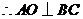 .
.
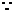 在正三棱柱
在正三棱柱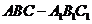 中,
中,
平面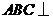 平面
平面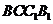 ,
,
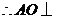 平面
平面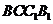 .
.
取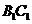 中点
中点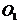 ,以
,以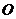 为原点,
为原点,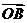 ,
,
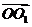 ,
,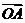 的方向为
的方向为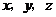 轴的正方向建立空间直角坐标系, ……2分
轴的正方向建立空间直角坐标系, ……2分
则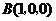 ,
,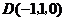 ,
,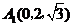 ,
,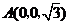 ,
,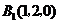 ,
,
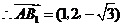 ,
,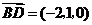 ,
,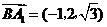 .
.
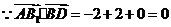 ,
,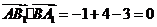 ,
……4分
,
……4分
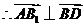 ,
,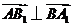 .
.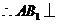 平面
平面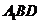 . ……5分
. ……5分
(Ⅱ)设平面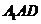 的法向量为
的法向量为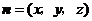 . ……6分
. ……6分
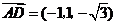 ,
,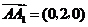 .
.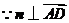 ,
,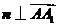 ,
,
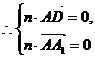
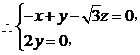
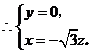 ……8分
……8分
令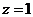 得
得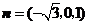 为平面
为平面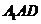 的一个法向量. …….9分
的一个法向量. …….9分
由(Ⅰ)知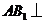 平面
平面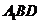 ,
,
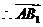 为平面
为平面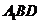 的法向量.……10分
的法向量.……10分
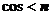 ,
, ……11分
……11分
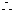 二面角
二面角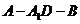 的大小为
的大小为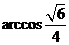 . ……12分
. ……12分
20.(12分)(1)设圆C方程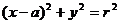 代入A、B两点坐标,得
代入A、B两点坐标,得
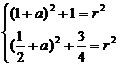 解得
解得 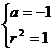
∴圆C: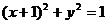 ……5分
……5分
(2)设过点Pn(n,0)的圆C的切线方程为
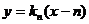 ……6分
……6分
即 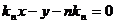 又圆心C(-1,0)到切线距离等于圆的半径
又圆心C(-1,0)到切线距离等于圆的半径
∴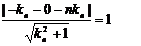 ……8分 即
……8分 即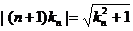
解得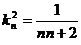 ……9分; 又可变形为:
……9分; 又可变形为: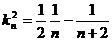 ……
10分
……
10分
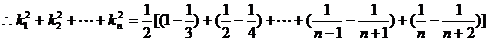
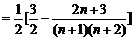 12分
12分
21 (14分)(1)设函数
(14分)(1)设函数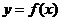 的图象上任一点
的图象上任一点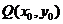 关于原点的对称点为
关于原点的对称点为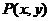 ,
,
则 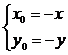 .
.
∵点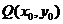 在函数
在函数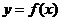 的图象上.
的图象上.
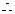
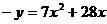 即
即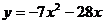 故
故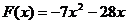
由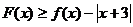 可得:
可得: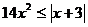
当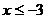 时,
时,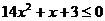 ,此时不等式无解
,此时不等式无解 
当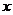
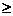
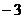 时,
时,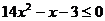 ,
,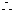
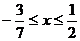
因此,原不等式的解集为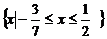 .
.
(另解: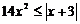 得
得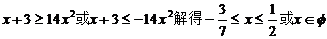
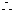
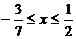 ,因此,原不等式的解集为
,因此,原不等式的解集为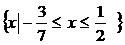 )
)
(2)依题意: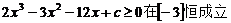
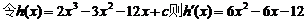

列表(略)
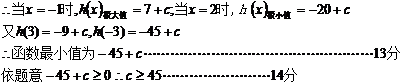
22.(12分)解:(1)已知|PF1|+|PF2|=10>|F1F2|=8,所以P点的轨迹是以2a=10为长轴,以F1、F2为焦点,而且焦点在y轴上的椭圆…..2分
即:a=5,c=4, 则b=3. 所以P点的轨迹方程为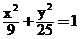 ……4分
……4分
(2)令M(x,y),Q(x1,y1),P(xo,yo),由已知M也为F2Q中点……5分
则有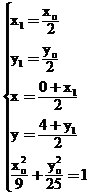 ……9分;
……9分;
得方程为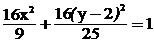 ……11分
……11分
故点M轨迹方程为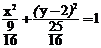 …….12分
…….12分