网址:http://www.1010jiajiao.com/paper/timu/5157903.html[举报]
17、(本小题满分12分)已知函数f(x)=(sinx-cosx)sinx+(3cosx-sinx)cosx,x∈R
(1)求f(x)的最小正周期;(2)当x∈[0,]时,求f(x)的最大值和最小值。
数学试题(理科)参考答案
一、CDACB DBDDB AC
二、13.3 14。-4
15。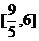 16。①②④
16。①②④
三、17.解:(1)
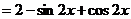
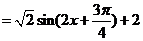 。
。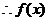 的最小正周期
的最小正周期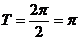 。
。
(2)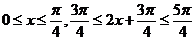

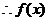 最大值是3,最小值是1。
最大值是3,最小值是1。
18. 解:(Ⅰ)记“厂家任取4件产品检验,其中至少有1件是合格品”为事件A
用对立事件A来算,有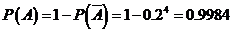
(Ⅱ)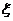 可能的取值为
可能的取值为
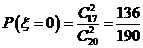 ,
,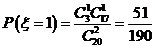 ,
,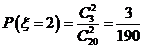
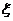 |
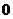 |
 |
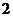 |
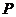 |
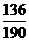 |
 |
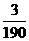 |
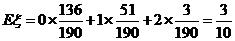
记“商家任取2件产品检验,都合格”为事件B,则商家拒收这批产品的概率
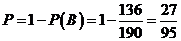 。所以商家拒收这批产品的概率为
。所以商家拒收这批产品的概率为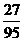
19.(解法一)(1)连结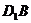 、
、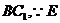 、
、 是
是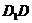 、
、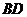 的中点,
的中点,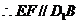 。
。
又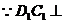 平面
平面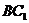 ,
,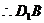 在平面
在平面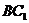 上的射影为
上的射影为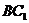 。
。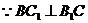 ,由三垂线定理知
,由三垂线定理知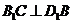 ,
,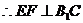 ,
,
(2)取DC的中点M,连结FM,则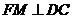 ,过M作
,过M作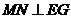 于N,连结FN,由三垂线定理可证得
于N,连结FN,由三垂线定理可证得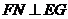 。
。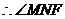 的邻补角为二面角
的邻补角为二面角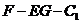 的平面角。
的平面角。
设正方体的棱长为4,则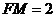 ,在
,在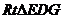 中,
中,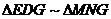 。
。
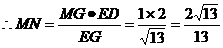 。在
。在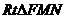 中,
中,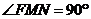
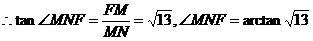
∴二面角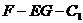 的大小为
的大小为 。
。
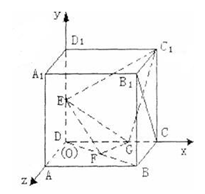 (解法二)如图建立空间直角坐标系
(解法二)如图建立空间直角坐标系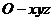 设正方体棱长为4,则
设正方体棱长为4,则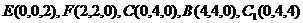 ,
,
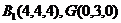
(1)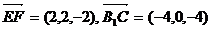
 ,
,
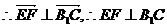 。
。
(2)平面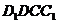 的一个法向量为
的一个法向量为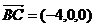 ,设平面
,设平面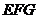 的一个法向量为
的一个法向量为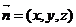 。
。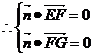 即
即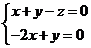 令
令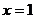 ,则
,则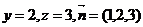
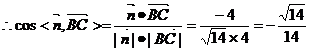
∴二面角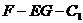 的大小为
的大小为 。
。
20.解:(1)当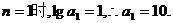 同样得
同样得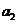 =100,
=100,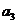 =1000
=1000
由已知 ①
①
当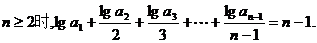 ②
②
①-②得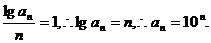 又
又
(2)设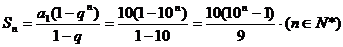
由
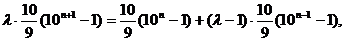
整理得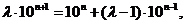
两边同除以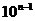 ,得
,得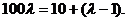 解得
解得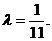
21.解:(1)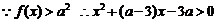
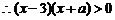 对
对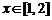 恒成立,
恒成立,
又 恒成立,
恒成立,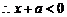 对
对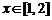 恒成立,
恒成立,
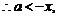 又
又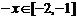 ,
,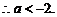
(2)由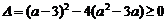 得:
得: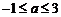 ,
,
不妨设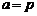 ,则q,r恰为方程两根,由韦达定理得:
,则q,r恰为方程两根,由韦达定理得:
①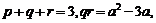
②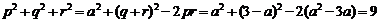
③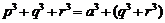
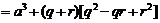
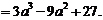
设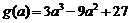 ,求导得:
,求导得: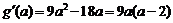
当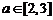 时,
时,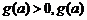 递增;当
递增;当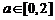 时,
时,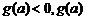 递减;
递减;
当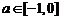 时,
时,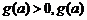 递增,
递增,
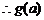 在
在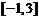 上的最小值为
上的最小值为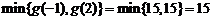
22.解:(1)设A、B两点的坐标分别为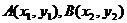
则由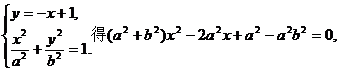
由韦达定理:得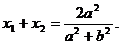
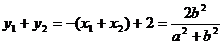
∴线段AB的中点坐标为
代入直线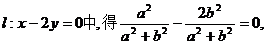
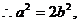
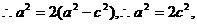
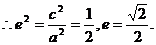
(2)由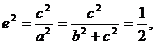
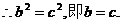
∴椭圆右焦点坐标为F(b,0),又设F(b,0)关于直线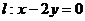 的对称点为
的对称点为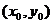 ,则有
,则有

点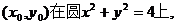
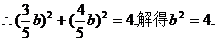
又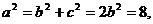 ∴所求椭圆方程为
∴所求椭圆方程为