
网址:http://www.1010jiajiao.com/paper/timu/5157965.html[举报]
20.(本小题满分12分)
设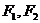 分别是椭圆的
分别是椭圆的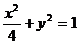 左,右焦点。
左,右焦点。
(Ⅰ)若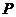 是第一象限内该椭圆上的一点,且
是第一象限内该椭圆上的一点,且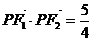
 ,
,
求点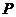 的坐标。
的坐标。
(Ⅱ)设过定点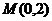 的直线与椭圆交于不同的两点
的直线与椭圆交于不同的两点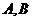 ,且
,且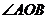 为锐角(其中O为坐标原点),求直线
为锐角(其中O为坐标原点),求直线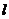 的斜率
的斜率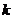 的取值范围。
的取值范围。
参考答案
一、选择题(本大题共4小题,每小题5分,共计20分
1.C 2.D 3.C 4.A 5.D 6.A 7.C 8.B 9.D 10.D 11.B 12.A
|
13.840 14.-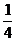 15.2或
15.2或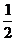 16.1234
16.1234
三、解答题 (本大题共6小题,共计70分)
17.(本小题满分10分)
解:(Ⅰ)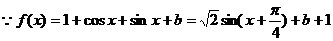 ,
,
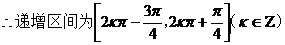 ……………………4分
……………………4分
(Ⅱ)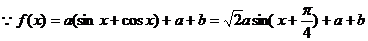
 …………6分
…………6分
而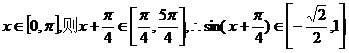 …………8分
…………8分
故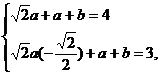
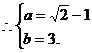 ………………………………10分
………………………………10分
18.(本小题满分12分)
解:(Ⅰ)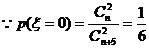 , …………………………………………3分
, …………………………………………3分
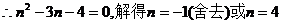 即袋中有4个黑球。
…………5分
即袋中有4个黑球。
…………5分
(Ⅱ)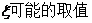 0, 1, 2, 3, 4。
0, 1, 2, 3, 4。
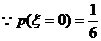 ,
,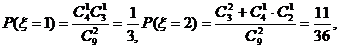
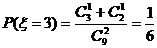 ,
,
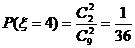 ……………………8分
……………………8分
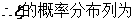
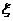 |
0 |
1 |
2 |
3 |
4 |
|
P |
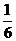 |
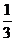 |
 |
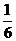 |
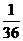 |
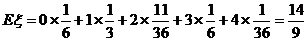 …………………………12分
…………………………12分
19.(本小题满分12分)
解法一:(Ⅰ)证明:连接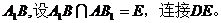
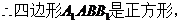
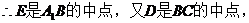
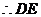 ∥
∥ 。 ……………………3分
。 ……………………3分
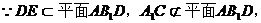
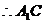 ∥平面
∥平面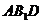 …………………………5分
…………………………5分
(Ⅱ)解:在平面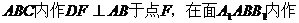
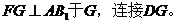
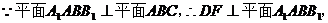
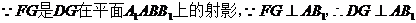
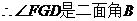 -
-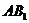 -
-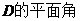 ……………………8分
……………………8分
设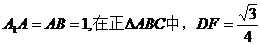 。
。
在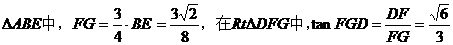
所以,二面角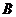 -
-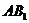 -
-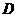 的大小为
的大小为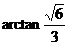 。 ………………12分
。 ………………12分
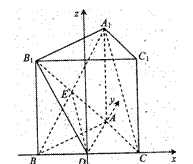
解法二:建立空间直角坐标系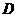 -
-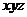 ,如图,
,如图,
(Ⅰ)证明:连接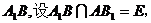 连接
连接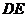 。设
。设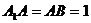
 则
则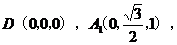
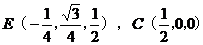
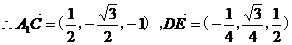
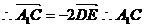 ∥
∥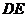 。
…………………………3分
。
…………………………3分
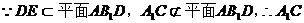 ∥平面
∥平面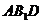 …………5分
…………5分
(Ⅱ)解:
设
故 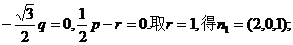
同理,可求得平面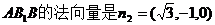 。………………9分
。………………9分
设二面角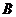 -
-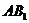 -
-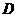 的大小为
的大小为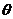
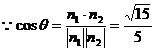
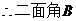
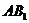
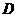 的大小为
的大小为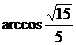 。……………………12分
。……………………12分
20.(本小题满分12分)
解:(Ⅰ)易知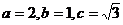 。
。
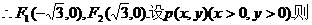
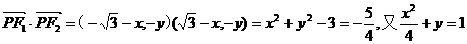 ,
,
………………………………3分
联立
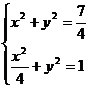 ,解得
,解得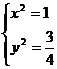
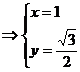 ,
,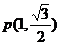 ………………5分
………………5分
(Ⅱ)显然 …………………………………………6分
…………………………………………6分
可设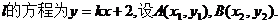
联立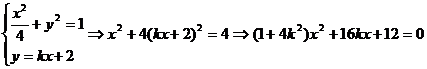
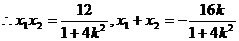 ……………………………………7分
……………………………………7分
由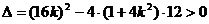
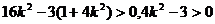
得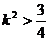 1 …………………………………………8分
1 …………………………………………8分
又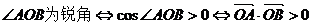 ,
,
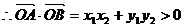 ………………………………………………9分
………………………………………………9分
又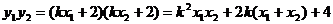
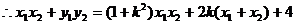
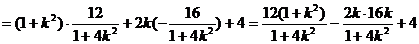
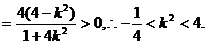 2 ……………………………………11分
2 ……………………………………11分
综12可知 …………12分
…………12分
21.(本小题满分12分)
解:(Ⅰ)由已知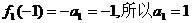 ……………………………………1分
……………………………………1分
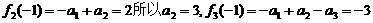 ,所以,
,所以,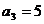 ……3分
……3分
(Ⅱ)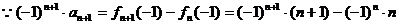
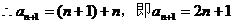
所以对于任意的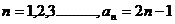 …………………………7分
…………………………7分
(Ⅲ)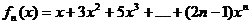
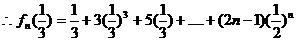 1
1
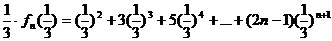 2
2
1-2,得
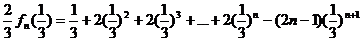 …………9分
…………9分
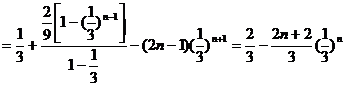
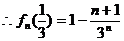 …………11分
又
…………11分
又 …………12分
…………12分
22.(本小题满分12分)
解.(Ⅰ) 
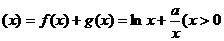
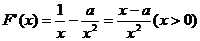
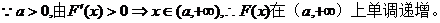
由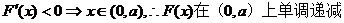 。
。
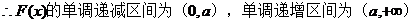
(Ⅱ)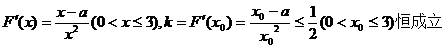
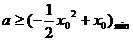 当
当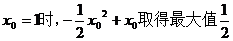
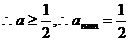 …………………………………………4分
…………………………………………4分
(Ⅲ)若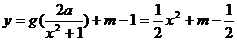 的图象与
的图象与
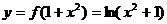 的图象恰有四个不同交点,
的图象恰有四个不同交点,
即 有四个不同的根,亦即
有四个不同的根,亦即
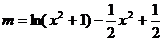 有四个不同的根。
有四个不同的根。
令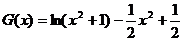 ,
,
则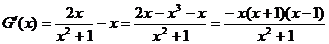 。
。
当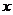 变化时
变化时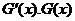 的变化情况如下表:
的变化情况如下表:
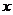 |
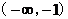 |
(-1,0) |
(0,1) |
(1,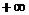 ) ) |
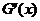 的符号 的符号 |
+ |
- |
+ |
- |
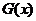 的单调性 的单调性 |
↗ |
↘ |
↗ |
↘ |
由表格知: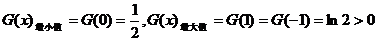 。
。
画出草图和验证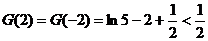 可知,当
可知,当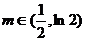 时,
时,
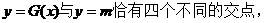

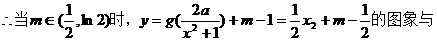
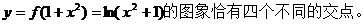 ………………4分
………………4分