
网址:http://www.1010jiajiao.com/paper/timu/5158288.html[举报]
22.(本小题满分14分)数列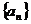 的各项均为正数,
的各项均为正数,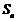 为其前
为其前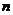 项和,对于任意
项和,对于任意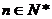 ,总有
,总有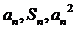 成等差数列.
成等差数列.
(1)求数列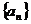 的通项公式;
的通项公式;
(2)若b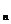 =a
=a 4
4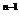 (
(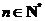 ), B
), B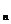 是数列{b
是数列{b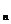 }的前
}的前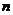 项和,
项和,
求证:不等式 B ≤4B
≤4B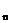 ,对任意
,对任意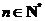 皆成立.
皆成立.
(3)令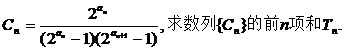
参考答案
一、选择题(1)A (2) C (3) B (4) B (5) C(6)C (7)D (8)C(9) D(10) C(11)D(12) D
二、填空题(13)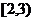 (14) 15 (15)
48 (16)
(14) 15 (15)
48 (16) 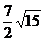
三、解答题
17. 解:(1)
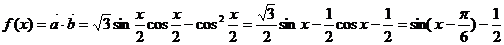 ……4分
……4分
由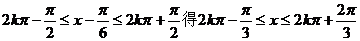
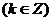
所以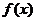 的单调递增区间为
的单调递增区间为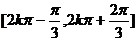
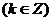 ………6分
………6分
(2)由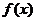 =
=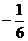 得:
得: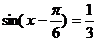
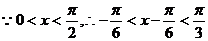
∴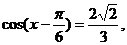 ………8分
………8分
∴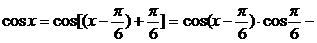
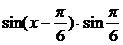
=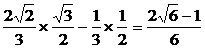 …………12分
…………12分
18. 解:1) 每位工人通过测试的概率为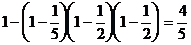 …………2分
…………2分
每位工人不能通过测试的概率为 .…………4分
.…………4分
3人中至少有一人不能通过测试的概率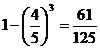 .…………6分
.…………6分
(2)
4位工人中恰有2人通过测试的概率为P=C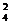 (
(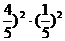 =
=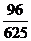 …………12分
。
…………12分
。
19. 解:(1)∵A1B1C1-ABC为直三棱柱 ∴CC1⊥底面ABC ∴CC1⊥BC
∵AC⊥CB ∴BC⊥平面A1C1CA ………………2分
∴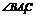 为
为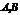 与平面A1C1CA所成角
与平面A1C1CA所成角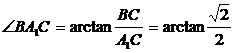
∴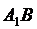 与平面A1C1CA所成角为
与平面A1C1CA所成角为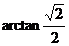 ……………4分
……………4分
(2)分别延长AC,A1D交于G. 过C作CM⊥A1G 于M,连结BM
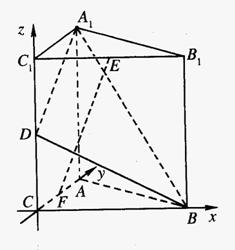 ∵BC⊥平面ACC1A1
∴CM为BM在平面A1C1CA的内射影
∵BC⊥平面ACC1A1
∴CM为BM在平面A1C1CA的内射影
∴BM⊥A1G ∴∠CMB为二面角B-A1D-A的平面角……6分
平面A1C1CA中,C1C=CA=2,D为C1C的中点
∴CG=2,DC=1 在直角三角形CDG中,
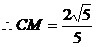
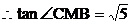 ,
,
即二面角B-A1D-A的大小为 …………………8分
…………………8分
(3)在线段AC上存在一点F,使得EF⊥平面A1BD………10分
其位置为AC中点,证明如下:
∵A1B1C1-ABC为直三棱柱 , ∴B1C1//BC
∵由(1)BC⊥平面A1C1CA,∴B1C1⊥平面A1C1CA
∵EF在平面A1C1CA内的射影为C1F ,F为AC中点 ∴C1F⊥A1D ∴EF⊥A1D ……11分
同理可证EF⊥BD, ∴EF⊥平面A1BD …………12分
∵E为定点,平面A1BD为定平面 ,点F唯一
解法二:(1)同解法一……………………4分
(2)∵A1B1C1-ABC为直三棱住 C1C=CB=CA=2 , AC⊥CB D、E分别为C1C、B1C1的中点, 建立如图所示的坐标系得
C(0,0,0) B(2,0,0) A(0,2,0)
C1(0,0,2) B1(2,0,2) A1(0,2,2)
D(0,0,1) E(1,0,2)………………6分
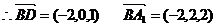 设平面A1BD的法向量为
设平面A1BD的法向量为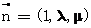
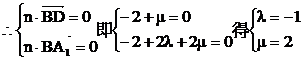
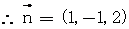 ……………8分
……………8分
平面ACC1A1的法向量为 =(1,0,0)
=(1,0,0) 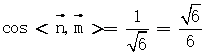 …9分
…9分
即二面角B-A1D-A的大小为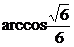 ……………10分
……………10分
(3)在线段AC上存在一点F,设F(0,y,0)使得EF⊥平面A1BD
欲使EF⊥平面A1BD 由(2)知,当且仅当 //
//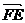 …………11分
…………11分
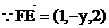
 … ……13分
… ……13分
∴存在唯一一点F(0,1,0)满足条件. 即点F为AC中点……12分
20.解:(1)设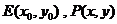 ,则
,则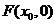 ,
,
∵点P分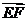 所成的比为
所成的比为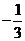 ∴
∴ 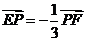
∴ 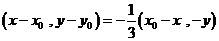
∴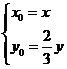
代入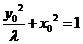 中,得
中,得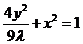 为P点的轨迹方程.
为P点的轨迹方程.
当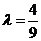 时,轨迹是圆。 ……6分
时,轨迹是圆。 ……6分
(2)由题设知直线l的方程为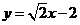 ,
设
,
设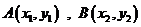
联立方程组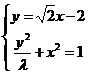 ,消去
,消去 得:
得: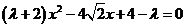 .
.
∵ 方程组有两解 ∴ 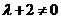 且
且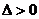 ∴
∴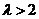 或
或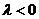 且
且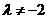 …………8分
…………8分
又已知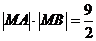 ,M、A、B三点共线,由向量知识得
,M、A、B三点共线,由向量知识得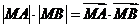 或
或
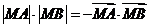 ,而
,而
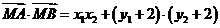
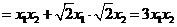 ∴
∴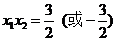
又 ∵ 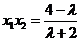 ∴
∴
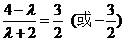 解得
解得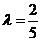 (舍去)或
(舍去)或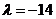
∴ 曲线C的方程是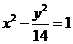 . ……………12分
. ……………12分
(21)解析:(1)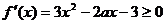 ………2分
………2分 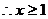
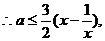
当x≥1时,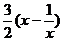 是增函数,其最小值为
是增函数,其最小值为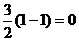
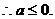 ………6分
………6分
(2)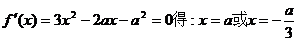
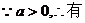
|
x |
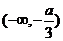 |
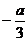 |
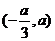 |
a |
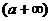 |
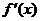 |
+ |
0 |
- |
0 |
+ |
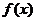 |
 |
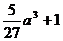 |
 |
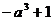 |
 |
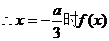 有极大值
有极大值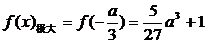
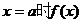 有极小值,
有极小值,
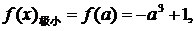 ………8分
………8分
∵若方程f(x)=(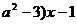 (a>0)至多有两个解,∴f(a)≥0或f(
(a>0)至多有两个解,∴f(a)≥0或f(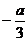 )≤0,
………10分
)≤0,
………10分
∴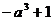 ≥0或
≥0或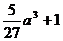 ≤0 (舍) 解得0<a≤1. ………12分
≤0 (舍) 解得0<a≤1. ………12分
(22)
(1)解:由已知:对于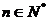 ,总有
,总有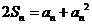 ①成立
①成立
∴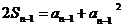 (n
≥ 2)② …………………2分
(n
≥ 2)② …………………2分
①--②得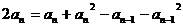 ,
∴
,
∴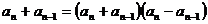
∵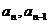 均为正数,∴
均为正数,∴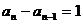 (n
≥ 2)
(n
≥ 2)
∴数列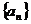 是公差为1的等差数列 ………3分, 又n=1时,
是公差为1的等差数列 ………3分, 又n=1时,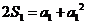 ,
,
解得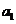 =1 ∴
=1 ∴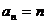 .(
.(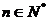 )
……4分
)
……4分
(2)b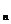 =
n+4
=
n+4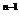 , 所以数列{b
, 所以数列{b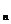 }的前
}的前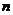 项和
项和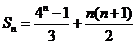 ……6分
……6分
∴对任意的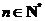 ,
,
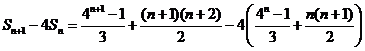
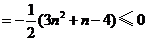 .……8分
.……8分
所以不等式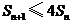 ,对任意
,对任意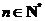 皆成立.(注:这里的S
皆成立.(注:这里的S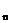 都换为B
都换为B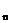 )
)
(3)由(1)知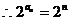
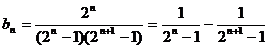 ………12分
………12分
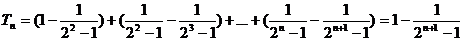 ………14分
………14分