
网址:http://www.1010jiajiao.com/paper/timu/5158362.html[举报]
22.(本小题满分14分)(文)椭圆 左、右焦点分别为
左、右焦点分别为 、
、 ,
, 是椭圆上一点,
是椭圆上一点,
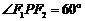 ,设
,设 .
.
(Ⅰ)求椭圆离心率 和
和 的关系式;
的关系式;
(Ⅱ)设 是离心率最小的椭圆上的动点,若
是离心率最小的椭圆上的动点,若 的最大值为
的最大值为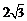 ,求椭圆的方程.
,求椭圆的方程.
(理)椭圆 左、右焦点分别为
左、右焦点分别为 、
、 ,
, 是椭圆上一点,
是椭圆上一点,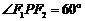 ,
,
设 .
.
(Ⅰ)求椭圆离心率 和
和 的关系式;
的关系式;
(Ⅱ)过 点离心率最小的椭圆的切线,交
点离心率最小的椭圆的切线,交 轴于
轴于 点,求证:
点,求证: .
.
参考答案
命题人:徐唐藩 校对:涂彩琴 方肇飞 编审:高三数学组
一.选择题(本大题12个小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项符合要求)
|
题号 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
|
答案 |
D |
文B 理B |
B |
A |
C |
文B 理D |
C |
B |
C |
文D 理A |
B |
文A 理B |
提示:(文)
12.(文)由二次函数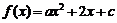 的值域是
的值域是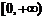 ,得
,得 且
且 ,∴
,∴ 且
且
 ,
, .∴
.∴ .当
.当 时取等号.
时取等号.
(理)提示:由二次函数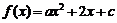 的值域是
的值域是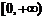 ,得
,得 且
且 ,∴
,∴ 且
且
 ,
, .∴
.∴ .
.
当 时取等号.
时取等号.
二.填空题(本大题4个小题,每小题4分,共16分,把答案填在题中横线上)
13.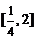 14.(文)
14.(文) (理)
(理) 15.
15. 16.
16.
三.解答题(本大题6个小题,共74分,解答题应写出文字说明、证明过程或演算步骤)
17.(本小题满分12分)解:(Ⅰ)由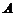 、
、 、
、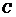 成等差数列及
成等差数列及 ,知
,知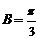 .
.
∵ ,∴
,∴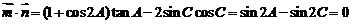 .由
.由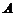 、
、 、
、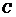 为三角形
为三角形
内角,且 ,∴
,∴ ,故
,故 为等边三角形.
为等边三角形.
(Ⅱ) ,
,
∴当 时,
时, 取得最大值
取得最大值 ,此时,
,此时,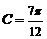 ,
,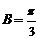 .
.
18.(本小题满分12分)(文) 解:(Ⅰ)由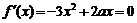 ,得
,得 或
或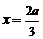 .
.
当 ,
, 变化时,
变化时, 、
、 的变化如下表:
的变化如下表:
 |
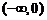 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
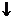 |
 |
 |
 |
 |
∴ ,
, ,解得
,解得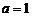 ,
,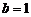 .∴
.∴ .
.
(Ⅱ)由题意,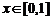 时,恒有
时,恒有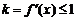 ,即
,即 恒成立.∵
恒成立.∵ ,当且仅当
,当且仅当
 时取等号,∴
时取等号,∴ ,故
,故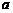 的取值范围为
的取值范围为 .
.
(理)解:(Ⅰ) ,令
,令 得
得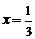 或
或 (舍去)
(舍去)
∴当 时,
时, 单调递增;当
单调递增;当 时,
时, 单调递减.
单调递减.
∴ 为函数
为函数 在
在 上的极大值.
上的极大值.
(Ⅱ)由 得,
得, 或
或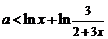 .
.
设 ,
, ,依题意知
,依题意知 或
或
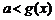 在
在 上恒成立, ∵
上恒成立, ∵ ,
,
 ,∴
,∴ 与
与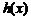 都在
都在 上单增,要使不等式①
上单增,要使不等式①
成立,当且仅当 或
或 ,即
,即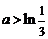 或
或 .
.
19.(本小题满分12分)(文)解:(Ⅰ) .
.
(Ⅱ) 或
或 .
.
(理)解:(Ⅰ)取卡片次数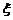 的可能值为
的可能值为 .∴
.∴ .
. 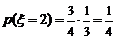 ,
,
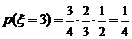 ,
, .故
.故 .
.
 .
.
(Ⅱ)设有放回抽取卡片时,取卡片次数为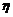 ,则
,则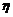 的可能值为
的可能值为 .
.
∵ ,
,
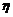 |
 |
 |
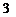 |
 |
 |
 |
 |
 |
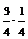 |
 |
 |
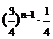 |
 |
∴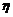 的分布列为:
的分布列为:
∴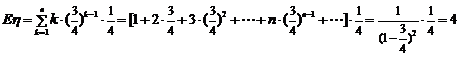 .
.
20.(本小题满分12分)解:(Ⅰ)延长 、
、 相交于点
相交于点 ,连结
,连结 ,则二面角
,则二面角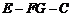
的大小为所求.作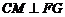 于点
于点 ,连结
,连结 ,由三垂线定理知
,由三垂线定理知
 .∴
.∴ 为所求二面角的大小.由已知
为所求二面角的大小.由已知 ,
, ,
,

 .由余弦定理得,
.由余弦定理得,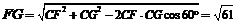 .
.
∴ ,可得
,可得 .
.
在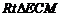 中,
中, ,则所求角为
,则所求角为 .
.
(Ⅱ)由已知矩形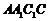 的面积为
的面积为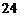 ,
, ,
, ,
, ,
,
∴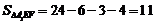 .取
.取 的中点
的中点 ,则
,则 .
.
作 交
交 于点
于点 ,可得
,可得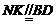 ,∴
,∴ 平面
平面 ,
, .由
.由 ,
,
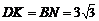 ,得
,得
 .设所求距离为
.设所求距离为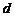 ,则由
,则由 得,
得,
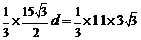 ,∴
,∴ 为所求.
为所求.
21.(本小题满分12分)
(文)解:(Ⅰ) .∵
.∵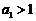 ,
,
∴ .又
.又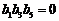 ,若
,若 ,则
,则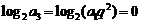 ,即
,即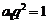 ,这与
,这与
矛盾,故 .∴
.∴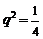 ,
, ,
,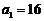 .∴
.∴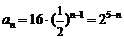 .
.
(Ⅱ)∵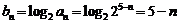 ,∴
,∴ 是首项为
是首项为 ,公差为
,公差为 的等差数列,∴
的等差数列,∴ ,
,
 .故
.故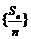 是首项为
是首项为 ,公差为
,公差为 的等差数列.∵
的等差数列.∵ 时,
时, ;
; 时,
时, ;
;
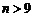 时,
时,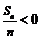 .故当
.故当 或
或 时,
时, 最大.
最大.
(理)解:(Ⅰ)∵ ,∴
,∴ .
.
∴ .
.
(Ⅱ)由(Ⅰ)知 ,∴
,∴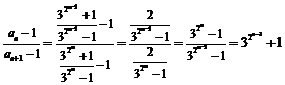 .
.
∴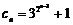 .
.
(Ⅲ)∵当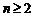 时,
时, ,当且仅当
,当且仅当 时取等号.且
时取等号.且 ,
,
故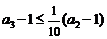 ,
,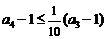 ,……,
,……,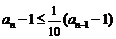 . 以上
. 以上 个式子相加,
个式子相加,
得 ,∴
,∴ ,
,
∴ ,∴
,∴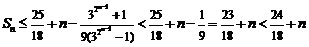 .
.
故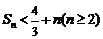 得证.
得证.
22.(本小题满分14分)(文)解:(Ⅰ) ,
, ,∴
,∴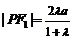 ,
,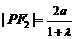 .
.
由余弦定理, ,得
,得 .
.
(Ⅱ)由(Ⅰ)知 ,
, ,
,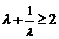 ,∴
,∴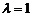 时,
时,
 的最小值为
的最小值为 .当
.当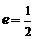 时,
时, .可设椭圆的方程
.可设椭圆的方程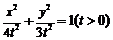 此时由
此时由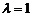 得,
得,
 ,∴
,∴ .设
.设 ,则
,则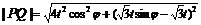
 .当
.当 时,
时, 的最大值为
的最大值为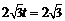 ,
,
∴ ,故椭圆的方程
,故椭圆的方程 .
.
(理)解:(Ⅰ) ,
, ,∴
,∴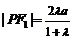 ,
,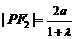 .由余弦定理,
.由余弦定理,
 ,得
,得 .
.
(Ⅱ)由(Ⅰ)知 .设
.设 ,知
,知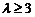 时,
时, 在
在
 上单调递增,∴
上单调递增,∴ 时,
时, ,得
,得 .设
.设 ,则
,则 ,
, .不妨设
.不妨设
点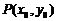 在第一象限.由
在第一象限.由 ,
,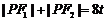 得,
得, ,∴
,∴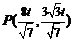 .
.
设 是椭圆上动点,则
是椭圆上动点,则 ,相减得
,相减得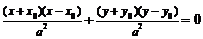 ,
,
即 .则
.则 时,
时,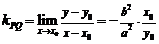 .设切线
.设切线 的方程为:
的方程为:
 ①, 又
①, 又 ②. 将②代入①整理得,
②. 将②代入①整理得,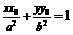 .
.
令 得,
得, ,∴
,∴ .又
.又 ,故
,故 .
.