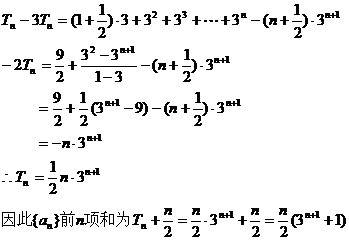网址:http://www.1010jiajiao.com/paper/timu/5158381.html[举报]
20.(理)已知函数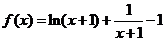 ,
,
(1)求函数 的单调递增区间;
的单调递增区间;
(2)若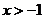 ,证明:
,证明: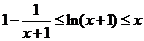 。
。
(文)已知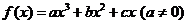 在
在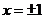 取得极值,且
取得极值,且 ,
,
(1)试求常数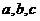 的值;
的值;
(2)试判断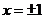 是函数的极大值还是极小值,并说明理由。
是函数的极大值还是极小值,并说明理由。
参考答案
第I卷(选择题,共60分)
|
1.D 2.B 3.C 4.C 5.D 6.A 7.B 8.A 9.B 10.(理)A 文(D)
11.D 12.C
第II卷(非选择题,共90分)
二、填空题(本大题共4小题,每小题4分,共16分)
13.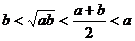 14.11
14.11
15.(理)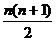 (文)[-1,1] 16.-
(文)[-1,1] 16.-
三、解答题(本大题共6小题,前五题每小题12分,22题14分,共74分)
17.解:(1)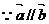
∴存在实数k,解得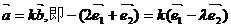
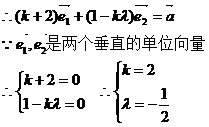
(2)由已知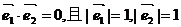
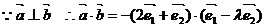
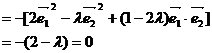
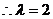
18.解:(1)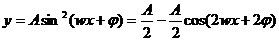
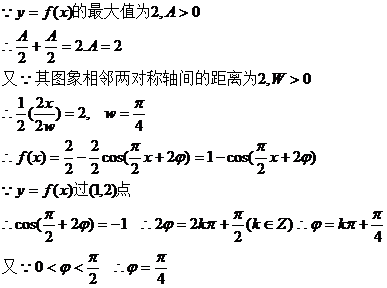
|
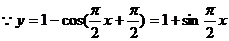

19.证明:(1)∵N是PB的中点
PA=PB ∴AN⊥PB
∵AD⊥平面PAB, ∴AD⊥PB
从而PB⊥平面ADMN
∵DM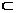 平面ADMN
平面ADMN
∴PB⊥DM
解:(2)取AD中点为G,连结BG,NG,则BG//CD
∴BG与平面ADMN所成的角和CD与平面ADMN所成的角相等
∵PB⊥平面ADMN
∴∠BGN是BG与平面ADMN所成的角
在Rt△BGN中,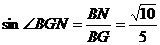
故CD与平面ADMN所成的角是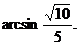
20.解:(理)(1)由题意,得x+1>0,x>-1
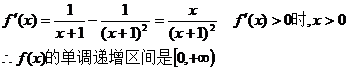
(2)由(1)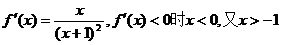
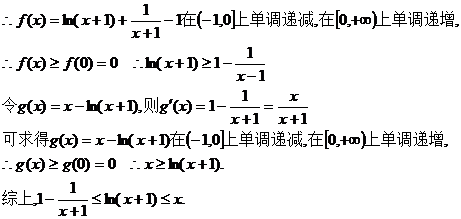
(文)(1)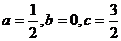
(2)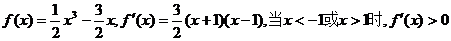 ,
,
当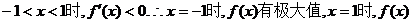 有极小值。
有极小值。
|
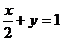 。
。
由题意得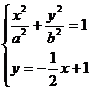 有唯一解
有唯一解
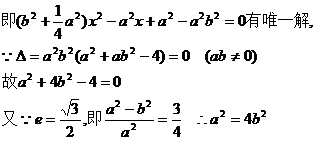
从而得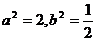 ,
,
故所求的椭圆方程为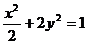
(2)由(1)得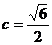
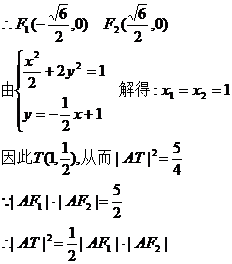
22.解:(1)由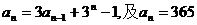 ,知
,知
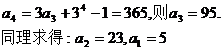
(2)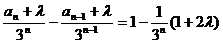
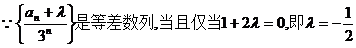
(3)由(2)得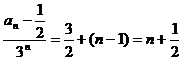
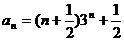
先求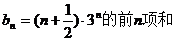
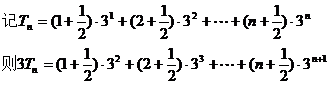
由上两式相减