
网址:http://www.1010jiajiao.com/paper/timu/5158476.html[举报]
22. (本小题满分14分)已知函数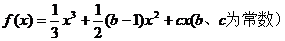 .
.
(1)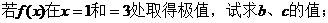
(2)若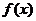 在
在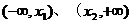 上单调递增,且在
上单调递增,且在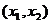 上单调递减,又满足
上单调递减,又满足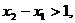 求证:
求证: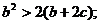
(3)在(2)的条件下,若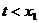 ,试比较
,试比较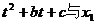 的大小,并加以证明。
的大小,并加以证明。
答 案
一、选择题(本大题共12小题,每题5分,满分60分)
1.B 2.D 3.D 4.B 5.A 6.A 7.B 8.D 9.C 10.C 11.D 12.C
二、填空题(本大题4共小题,每题4分,满分16分)
13.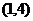 14.
14.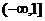 15.(理)[2,2
15.(理)[2,2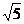 ] (文)[4,
] (文)[4,
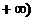 16.①②③④⑤
16.①②③④⑤
三、解答题:本大题共6小题,共74分。解答应写出文字说明,证明过程或演算步骤。
17.解:当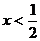 时,原不等式变形为
时,原不等式变形为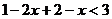 ,解得
,解得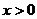

当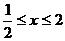 时,原不等式变形为
时,原不等式变形为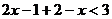 ,解得
,解得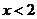
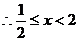
当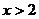 时,原不等式变形为
时,原不等式变形为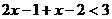 ,解得
,解得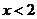
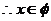
综上,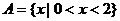 6分
6分
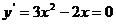 ,解得
,解得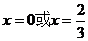
当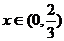 时,
时,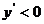 ;
;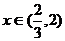 时,
时,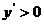
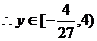 即
即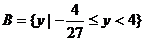
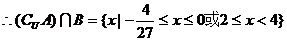 . 12分
. 12分
18.(1)证明:
 =log
=log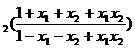
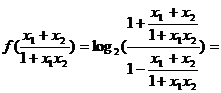 log
log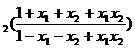

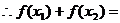
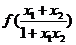 。 6分
。 6分
(2)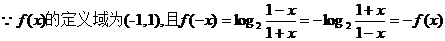
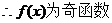 。
。
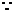
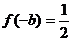 ,
,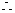
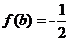 由(1)得
由(1)得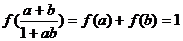
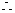
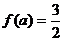 12分
12分
19.解:(I)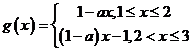
(1)当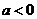 时,函数
时,函数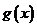 是
是 增函数,
增函数,
此时,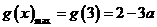 ,
,
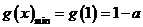 ,所以
,所以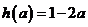 ;--2分
;--2分
(2)当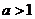 时,函数
时,函数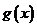 是
是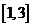 减函数,此时,
减函数,此时,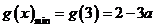 ,
,
 ,所以
,所以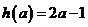 ;----4分
;----4分
(3)当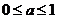 时,若
时,若 ,则
,则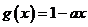 ,有
,有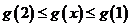 ;
;
若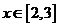 ,则
,则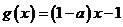 ,有
,有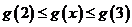 ;
;
因此,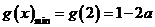 ,----6分
,----6分
而 ,
,
故当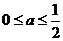 时,
时,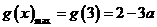 ,有
,有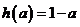 ;
;
 当
当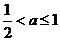 时,
时, ,有
,有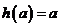 ;----8分
;----8分
综上所述: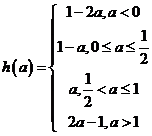 。----9分
。----9分
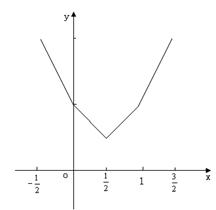
(II)画出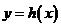 的图象,如右图。----11分
的图象,如右图。----11分
数形结合,可得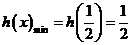 。----12分
。----12分
20.解:由题设知,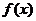 在
在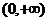 是增函数,且
是增函数,且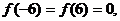 故在
故在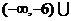
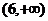 上
上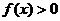 ,
,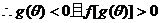 等价于
等价于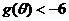 . 3分
. 3分
即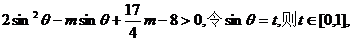
设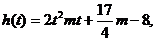 原问题等价于:函数
原问题等价于:函数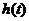 在区间
在区间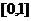 最小值大于0。 5分
最小值大于0。 5分
(i)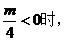 函数
函数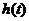 在区间
在区间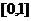 最小值为
最小值为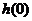
 矛盾 7分
矛盾 7分
(ii)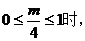 函数
函数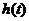 在区间
在区间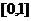 最小值为
最小值为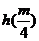 ,
,
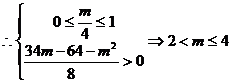 .
9分
.
9分
(iii)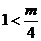 时,函数
时,函数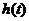 在区间
在区间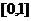 最小值为
最小值为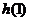 ,
,
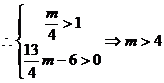 11分
11分
综上: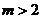 12分
12分
21.(理)解:(1)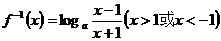 3分
3分
(2)设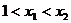 ,∵
,∵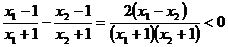
∴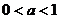 时,
时,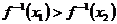 ,∴
,∴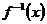 在
在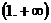 上是减函数:
上是减函数:
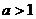 时,
时,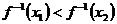 ,∴
,∴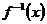 在
在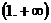 上是增函数。7分
上是增函数。7分
(3)当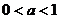 时,∵
时,∵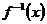 在
在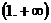 上是减函数
上是减函数
∴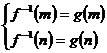 ,由
,由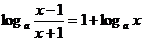 得
得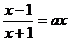 ,
,
即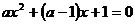 ,
,
可知方程的两个根均大于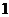 ,即
,即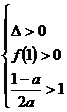
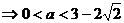 10分
10分
当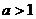 时,∵
时,∵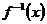 在
在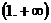 上是增函数
上是增函数
∴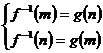
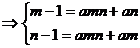
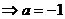 (舍去)。
(舍去)。
综上,得 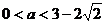 。
12分
。
12分
(文)解:(1)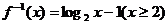 2分
2分
设 为函数
为函数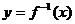 图象上任意一点,
图象上任意一点,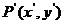 为平移后的对应点,则
为平移后的对应点,则
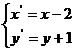 解得
解得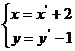 且
且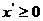 4分
4分
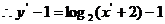
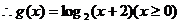 6分
6分
(2)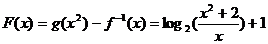
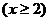 8分
8分
设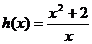 =
= ,令
,令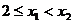 ,
,
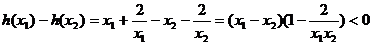
 10分
10分
当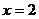 时,
时,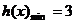 ,故当
,故当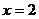 时,
时,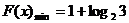 12分
12分
22.解:(1)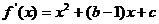
根据题意,1和3是方程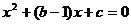 的两根,
的两根,
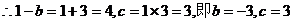 .
4分
.
4分
(2)由题意知,当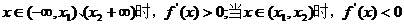 ,
,
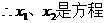
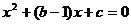 的两根,
的两根,
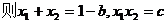
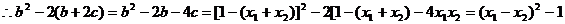
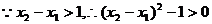 ,
, 即
即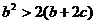 . 8分
. 8分
(3)在(2)的条件下,由上题知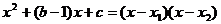
即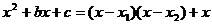
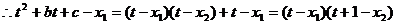
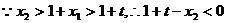 ,又
,又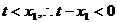
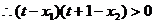 ,故
,故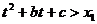 14分
14分