
网址:http://www.1010jiajiao.com/paper/timu/5158726.html[举报]
11.某学校开设10门选修课程,其中3门是技能类课程,2门是理论类课程.学校规定每位学生应选修4门,且技能类课程和理论类课程每类至多选修1门,则不同的选修方法种数是( )
A.50 B.100 C.11O D.115
数学(理科)试题参考答案及评分标准
说明:
一、本解答指出了每题要考查的主要知识和能力,并给出了一种或几种解法供参考,如果考生的解法与本解答不同,可根据试题的主要考查内容比照评分标准制定相应的评分细则.
二、对计算题,当考生的解答在某一步出现错误时,如果后继部分的解答未改变该题的内容和难度,可视影响的程度决定后继部分的给分,但不得超过该部分正确解答应给分数的一半;如果后继部分的解答有较严重的错误,就不再给分.
三、解答右端所注分数,表示考生正确做到这一步应得的累加分数.
四、只给整数分数.选择题和填空题不给中间分.
一、选择题:本题考查基础知识和基本运算,每小题5分,满分60分.
1.A 2.C 3.C 4.B 5.A 6.D 7.B 8.D 9.A 10.D 11.D 12.A
二、填空题:本题考查基础知识和基本运算。每小题4分。满分16分.
13.15;14.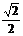 ;15.
;15.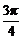 ;16.
;16.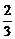
三、解答题:本大题共6小题,共74分。解答应写出文字说明,证明过程或演算步骤.
17.本小题主要考查三角函数的倍角公式、和角公式,三角函数的图象与性质等基础知识;考查理解能力和运算能力.满分12分.
解: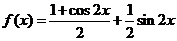 ……………………………………………………(4分)
……………………………………………………(4分)
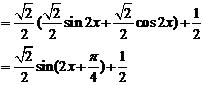 ………………………………………(6分)
………………………………………(6分)
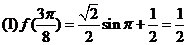 …………………………………………………(8分)
…………………………………………………(8分)
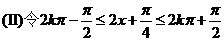 …………………………………………(10分)
…………………………………………(10分)
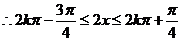
即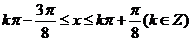 时,f(x)单调递增.
时,f(x)单调递增.
∴f(x)单调递增区间为[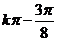 ,
,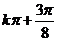 ]
]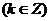 ……………………(12分)
……………………(12分)
18.本小题主要考查等差数列、等比数列、数列求和等基础知识考查化归与转化的思想方
法;考查推理与运算能力.满分12分.
解法一:(I)  ,且a1=1,显然an≠0
,且a1=1,显然an≠0
 ,又c为常数,
,又c为常数,
∴数列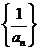 是等差数列. ………………………………………………(4分)
是等差数列. ………………………………………………(4分)
(Ⅱ)由(Ⅰ)知,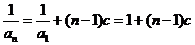 ……………………………(5分)
……………………………(5分)
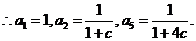
又∵a1,a2,a5成等比数列,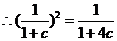 ,解得c=0或c=2. (7分)
,解得c=0或c=2. (7分)
当c=0时,an+1=an,不合题意,舍去.
∴c=2. ……………………………………………………………………(8分)
(Ⅲ)由(Ⅱ)知c=2,∴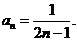 …………………………………………(9分)
…………………………………………(9分)

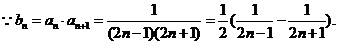 …………(10分)
…………(10分)
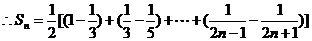
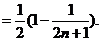 ……………………………………………………(11分)
……………………………………………………(11分)
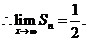 .…………………………………………………………(12分)
.…………………………………………………………(12分)
解法二:(Ⅰ)  ,且a1=1,显然an≠0
,且a1=1,显然an≠0
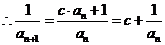 ,……………………………………………(2分)
,……………………………………………(2分)
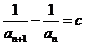 ,又c为常数,
,又c为常数,
∴数列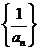 是等差数列……………………………………………(4分)
是等差数列……………………………………………(4分)
(Ⅱ)、(Ⅲ)解法同解法一.
19.本小题主要考查直线与直线、直线与平面的位置关系、二面角的概念等基础知识;考查空间想象能力。逻辑思维能力和探索问题、解决问题的能力.满分12分.
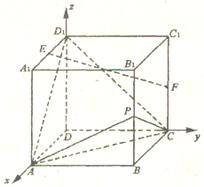 解法一:如图分别以DA、DC、DD1所在的直线为x 轴、
解法一:如图分别以DA、DC、DD1所在的直线为x 轴、
y轴、z轴建立空间直角坐标系D-xyz,由已知
得D(0,0,0)、A(2,0,0)、B(2,2,0)、
C(0,2,0)、B1(2,2,2)、D1(0,0,2)、
E(1,0,2 )、F(0,2,1).…………(2分)
(Ⅰ)易知平面ACD1的一个法向量是
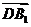 =(2,2,2). …………………(4分)
=(2,2,2). …………………(4分)
又∵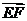 =(-1,2,-1),
=(-1,2,-1),
由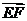 .
.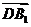 = -2+4-2=0,
= -2+4-2=0,
∴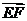 ⊥
⊥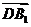 ,而EF
,而EF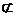 平面ACD1,
平面ACD1,
∴EF∥平面ACD1……………………………………………………(6分)
(Ⅱ) ∵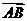 =(0,2,0),cos<
=(0,2,0),cos<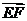 ,
,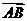 >=
>=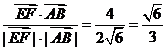
∴异面直线EF与AB所成的角为arccos ……………………(8分).
……………………(8分).
(Ⅲ)设点P(2,2,t)(0<t≤2),平面ACP的一个法向量为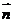 =(x,y,z),
=(x,y,z),
则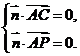
∵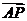 =(0,2,t),
=(0,2,t), 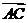 =(-2,2,0),
=(-2,2,0),
∴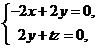 取
取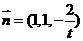 .
.
易知平面ABC的一个法向量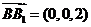 ,
,
依题意知,<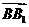 ,
,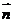 >=30°或<
>=30°或<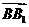 ,
,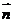 >=150°,
>=150°,
∴|cos<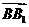 ,
,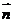 >|=
>|=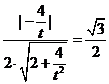 ………………………(10分)
………………………(10分)
即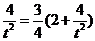 ,解得
,解得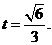
∵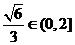 ,∴在棱BB1上存在一点P,当BP的长为
,∴在棱BB1上存在一点P,当BP的长为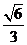 时,
时,
二面角P-AC-B的大小为30°. ……………………………(12分)
解法二:(Ⅰ)同解法一知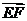 =(-1,2,-1) ,
=(-1,2,-1) ,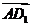 =(-2,0,2),
=(-2,0,2),
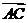 = (-2,2,0),∴
= (-2,2,0),∴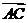 -
-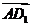 =
=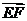 ,
,
∴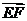 、
、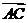 、
、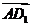 共面.
共面.
又∵EF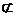 平面ACD1,∴EF∥平面ACD1. ……………………………(4分)
平面ACD1,∴EF∥平面ACD1. ……………………………(4分)
(Ⅱ)、(Ⅲ)同解法一.
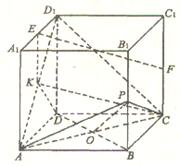 解法三:(Ⅰ)取AD1的中点K,连结EK、KC,在△AA1D1
解法三:(Ⅰ)取AD1的中点K,连结EK、KC,在△AA1D1
中,EK∥AA1,且EK=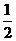 AA1,
AA1,
|
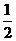 CC1,CC1∥AA1,∴FC EK,
CC1,CC1∥AA1,∴FC EK,
∴四边形EKCF为平行四边形,
∴EF∥CK.又∵CK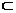 平面ACD1,
平面ACD1,
EF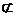 平面ACD1,∴EF∥平面ACD1. (4分)
平面ACD1,∴EF∥平面ACD1. (4分)
(Ⅱ)由(Ⅰ)知EF∥CK,又AB∥CD,
∴∠DCK就是异面直线AB和EF所成的角(或补角).
连DK,∵CD⊥平面AD1,DK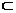 平面AD1,
平面AD1,
∴CD⊥DK,在Rt△CDK中,DC=2,DK=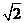 ,∴tan∠DCK=
,∴tan∠DCK=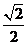 ,
,
∴异面直线AB和EF所成的角为arctan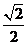 .…………………(8分)
.…………………(8分)
(Ⅲ)假设存在点P,使得二面角P-AC-B的大小为30°.连结BD交AC于O 点,连结OP,∵ABCD为正方形,∴BO⊥AC,而OB为OP在平面AC上的射影,由三垂线定理得OP⊥AC,
∴∠BOP为二面角P-AC-B的平面角,∴∠BOP=30°,
则tan30°=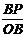 , ∴BP=
, ∴BP= 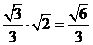
∵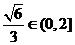 ∴在棱BB1上存在一点P,当BP的长为
∴在棱BB1上存在一点P,当BP的长为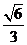 时,
时,
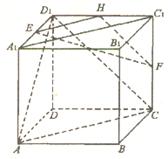 二面角P-AC-B的大小为30°. ……………………………………(12分)
二面角P-AC-B的大小为30°. ……………………………………(12分)
解法四:(Ⅰ)取D1C1的中点H,连结EH,FH,A1C1,
∵E为A1D1的中点,∴EH∥AlCl,
而A1C1∥AC,∴EH∥AC,
又∵F为CC1的中点,∴HF∥D1C.
∵EH与HF相交,D1C与AC相交,
∴平面EHF∥平面ACD1,EF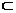 平面EHF,
平面EHF,
∴EF∥平面ACD1. ………………(4分)
(Ⅱ)、(Ⅲ)同解法三.
20.本小题主要考查函数与不等式等基础知识;考查运用数学知识分析问题和解决问题的能力.满分12分.
解法一:(Ⅰ)依题意设v=kω2,……………………………………………………(2分)
又当ω=3时,v=54000,∴k=6000,…………………………………(3分)
故vω2=6000ω2.………………………………………………………(4分)
(Ⅱ)设这颗钻石的重量为a克拉,
由(Ⅰ)可知,按重量比为l∶3切割后的价值为
6000(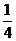 a)2+6000(
a)2+6000( a)2.…………………………………………… (6分)
a)2.…………………………………………… (6分)
价值损失为
6000a2一[6000(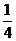 a)2+6000(
a)2+6000( a)2].…………………………………(7分)
a)2].…………………………………(7分)
价值损失的百分率为
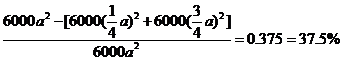
答:价值损失的百分率为37.5%.……………………………………(8分)
(Ⅲ)若把一颗钻石按重量比为m∶n切割成两颗,价值损失的百分率应为
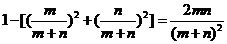 ,…………………………(10分)
,…………………………(10分)
又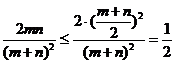 ,…………………………………(11分)
,…………………………………(11分)
等号当且仅当m=n时成立.
即重量比为1∶1时,价值损失的百分率达到最大………………(12分)
解法二:(Ⅰ)、(Ⅱ)同解法一.
(Ⅲ)设一颗钻石切割成两颗,其重量比为1∶x,
则价值损失的百分率为
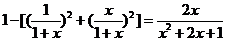 ,………………………………(10分)
,………………………………(10分)
又x>0,∴x2+1≥2x,
故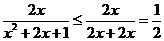
等号当且仅当x=1时成立.……………………………………………(11分)
故当重量比为1∶1时,价值损失的百分率达到最大………………(12分)
21.本小题主要考查抛物线的几何性质、直线与抛物线的位置关系等基础知识;考查解析几何的基本思想方法;考查分析问题、解决问题的能九满分12分.
解法一:(Ⅰ)设D(x,y),∵A(a,0),由ABCD为菱形
 且AC、BD的交点在y轴上,
且AC、BD的交点在y轴上,
∴B、C两点坐标为(-x,0)、(-a,y).
由AC⊥BD得
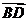 .
.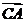 =(2x,y).(2a,-y)
=(2x,y).(2a,-y)
=4ax - y2=0,
即 y2 = 4ax. …………………………(4分)
注意到ABCD为菱形,∴x≠0
故轨迹E的方程为y2 = 4ax(x≠0).
……………………………………(5分)
(Ⅱ)∠PRQ不可能为钝角,即∠PRQ≤90°.
…………………………………(6分)
证明如下:
(1)当PQ⊥x轴时,P、Q点的坐标为(a,±2a),又R(一a,0),
此时∠PRQ=90°,结论成立;……………………………………(7分)
(2)当PQ与x轴不垂直时,设直线PQ的方程为y=k(x一a),
由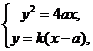 得 k2x2 - (2ak2+4a)x + k2a2 = 0
得 k2x2 - (2ak2+4a)x + k2a2 = 0
记P(x1,y1),Q(x2,y2),则x1+x2
=2a+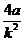 ,x1
x2=a2.
,x1
x2=a2.
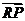 .
.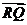 =(x1+a)(x2+a)+y1y2
=(x1+a)(x2+a)+y1y2
=(x1+a)(x2+a)+k2(x1- a)(x2- a)
=(1+k2) x1 x2+(a - ak2)( x1+x2)+a2+a2k2
=(1+k2) a2 +(a - ak2)( 2a+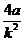 )+a2+a2k2=
)+a2+a2k2=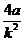 >0
>0
………………………………………………………(10分)
即<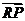 ,
,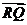 >为锐角,……………………………………………(11分)
>为锐角,……………………………………………(11分)
综上(1)、(2)知∠PRQ≤90°成立. …………………………(12分)
解法二:(Ⅰ)设D(x,y),由ABCD为菱形且AC、BD的交点在y轴上,
∴C点坐标为(-a,y),∵A(a,0),由|DA|=|DC|得
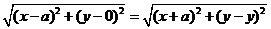 ,
,
化简得y2=4ax.………………………………………………………(4分)
注意到ABCD为菱形,∴x≠O,
故轨迹E的方程为y2=4ax(x≠O).……………………………………(5分)
(Ⅱ)∠PRQ不可能为钝角,即∠PRQ≤90°.……………………………(6分)
证明如下:
设P(x1,y1),Q(x2,y2),同证法一易知,则x1 x2=a2.又y12=4ax1,y22=4ax2,且|PR|2=x1+x2+2a ,因为
|PR|2+|QR|2-|PQ|2=(x1+a)2+y12+(x2+a)2+y22-( x1+x2+2a)2
=2ax1+2ax2-4a2≥2 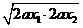 -4a2=4a
-4a2=4a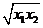 -4a2=0……………(9分)
-4a2=0……………(9分)
从而 cos∠PRQ=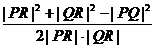 ≥0,……………………(11分)
≥0,……………………(11分)
即∠PRQ≤90°…………………………………………………………(12分)
解法三:(Ⅰ)因为ABCD为菱形,且AC与BD的交点在y轴上,
所以点C的横坐标为 -a,
即点C在直线x = -a上,从而D到C的距离等于D到直线x = -a的距 离.又ABCD为菱形,所以点D到点A的距离与点D到直线x = -a的距离 相等,即轨迹E为抛物线,方程为y2=4ax.…………………………(4分)
注意到ABCD为菱形,∴x≠O,
故轨迹E的方程为y2=4ax(x≠O).……………………………………(5分)
(Ⅱ) ∠PRQ不可能为钝角,即∠PRQ≤90°.……………………………(6分)
证明如下:
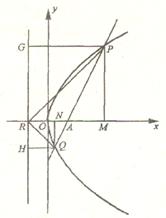
如图,过P、Q向x轴及准线x = -a引垂线,记垂足为M、N、C、H,
则|MR|=|PG|=|PA|≥|PM|,所以∠PRM≤45°,…………………(10分)
同理可证∠QRN≤45°,从而∠PRQ≤90°.…………………………(12分)
解法四:(Ⅰ)同解法一.
(Ⅱ) ∠PRQ不可能为钝角,即∠PRQ≤90°.………………………(6分)
证明如下:
设P(x1,y1),则y12=4ax1,tan∠PRM=|kPR|=|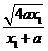 |=
|=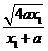 ,…(8分)
,…(8分)
∵x1+a≥2 ,∴tan∠PRA≤1,∠QRA≤45°,…………………(10分)
,∴tan∠PRA≤1,∠QRA≤45°,…………………(10分)
同理可证∠QRA≤45°,即∠PRQ≤90°.……………………………(12分)
22.本小题主要考查函数的导数、单调性、极值和不等式等基础知识;考查化归及数形结合的思想方法;考查分析问题、解决问题的能九满分14分.
解:(Ⅰ) 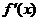 =
= 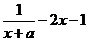 ………………………………………………………(2分)
………………………………………………………(2分)
∵x=0时,f(x)取得极值,∴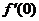 =0,……………………………………(3分)
=0,……………………………………(3分)
故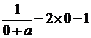 =0,解得a=1.经检验a=1符合题意. …………………(4分) (Ⅱ)由a=1知f(x)=ln(x+1)-x2 - x,由f(x)=
=0,解得a=1.经检验a=1符合题意. …………………(4分) (Ⅱ)由a=1知f(x)=ln(x+1)-x2 - x,由f(x)= 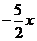 +b,
+b,
得ln(x+1)-x2+ 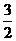 x-b=0,
x-b=0,
令φ(x)= ln(x+1)-x2+ 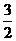 x-b,
x-b,
则f(x)= 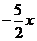 +b在[0,2]上恰有两个不同的实数根等价于φ(x)=0在[0,2]
+b在[0,2]上恰有两个不同的实数根等价于φ(x)=0在[0,2]
恰有两个不同实数根.………………………………………………………(5分)
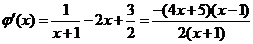 ,………………………………(8分)
,………………………………(8分)
当x∈(O,1)时,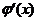 >O,于是φ(x)在(O,1)上单调递增;
>O,于是φ(x)在(O,1)上单调递增;
当x∈(1,2)时,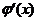 <0,于是φ(x)在(1,2)上单调递减.…………(8分)
<0,于是φ(x)在(1,2)上单调递减.…………(8分)
依题意有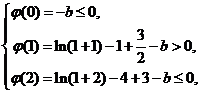
∴ln3 -1≤b<ln2 +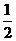 .…………………………………………………………(9分)
.…………………………………………………………(9分)
(Ⅲ) f(x)=ln(x+1)-x2 –x的定义域为{x|x> -1},………………………………(10分)
由(Ⅰ)知 ,……………………………………………(11分)
,……………………………………………(11分)
令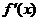 =0得,x=0或x= -
=0得,x=0或x= -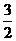 (舍去),
(舍去),
∴当-1<x<0时,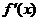 >0,f(x)单调递增;
>0,f(x)单调递增;
当x>0时,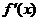 <0,f(x)单调递减.
<0,f(x)单调递减.
∴f(0)为f(x)在(-1,+∞)上的最大值. …………………………………(12分)
∴f(x)≤ f(0),故ln(x+1)-x2-x≤0(当且仅当x=0时,等号成立).…(13分)
对任意正整数n,取x= >0得,ln(
>0得,ln( +1)<
+1)<  +
+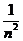 ,故ln(
,故ln(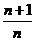 )<
)<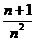 .
.
………………………………………………………………(14分)