
网址:http://www.1010jiajiao.com/paper/timu/5158755.html[举报]
21.(本小题满分12分)
设函数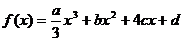 的图象关于原点对称,
的图象关于原点对称,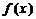 的图象在点
的图象在点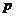 (1,
(1,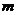 )处的切线的斜率为-6,且当
)处的切线的斜率为-6,且当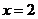 时
时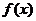 有极值.
有极值.
(1)求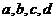 的值;
的值;
(2)若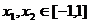 ,求证:
,求证: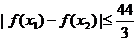 .
.
参考答案
一、选择题:
|
二、填空题:
13.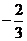 14.
14.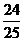 15.
15.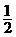 16.991
16.991
三、解答题:( 本大题共有6个小题,共74分。解答应写出文字说明、演算步骤或证明过程。)
17.解:
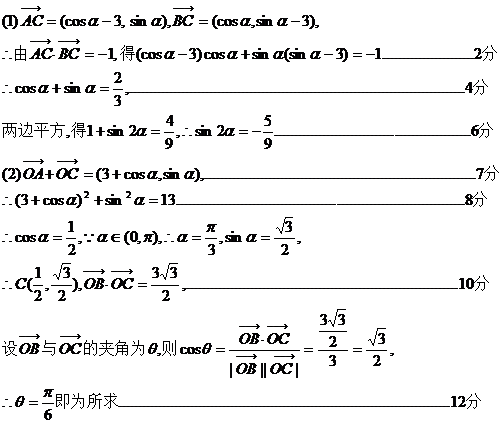
18.解:(1)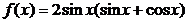 ………………………1分
………………………1分
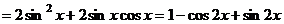
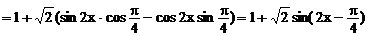 ………………2分
………………2分
所以函数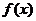 的最小正周期为π.………………………3分
的最小正周期为π.………………………3分

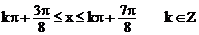
所以函数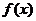 的单调递减区间为
的单调递减区间为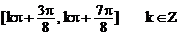 ……………5分
……………5分
(2)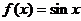
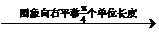
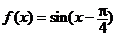
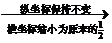

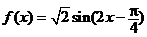
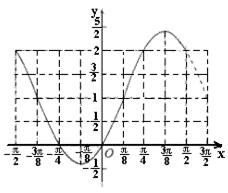
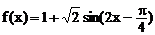 ………9分
………9分
(3)由(1)知
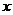 |
 |
 |
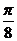 |
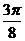 |
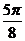 |
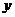 |
1 |
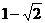 |
1 |
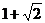 |
1 |
故函数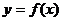 在区间
在区间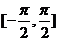 上
上
的图象是 ……………………12分
19.解:(1)当n = 1时,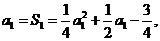 解得a1 =
3…………2分
解得a1 =
3…………2分
当n≥2时,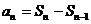 =
= 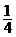 (an2
+ 2an-1-3)-
(an2
+ 2an-1-3)- 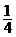 (
(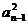 +
2an-3)………3分
+
2an-3)………3分
∴4an = an2-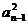 +
2an-2an-1
+
2an-2an-1
∴
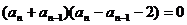
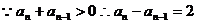 (
(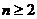 )…………5分
)…………5分
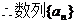 是以3为首项,2为公差的等差数列
是以3为首项,2为公差的等差数列
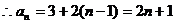 …………6分
…………6分
(2)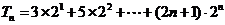 ①
①
又 ②
②
②-①
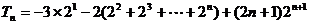
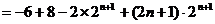
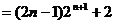
∴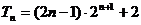 …………12分
…………12分
20.解:由题意知,每年的经费是以12为首项,4为公差的等差数列,设纯利润与年数的关系为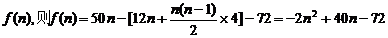 …2分
…2分
(1)纯利润就是要满足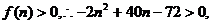 ………………4分
………………4分
解得 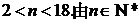 知从第三年开始获利 …………6分
知从第三年开始获利 …………6分
(2)①年平均利润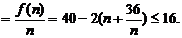 当且仅当n=6时等号成立.
当且仅当n=6时等号成立.
此方案共获利6×16+48=144(万美元),此时n=6,…………8分
②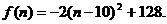 当n=10时,
当n=10时,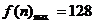 .
.
故第②种方案共获利128+16=144(万美元),……10分
故比较两种方案,获利都是144万美元。
但第①种方案只需6年,而第②种方案需10年,故选择第①方案更合算.……12分
21.解 (1)
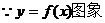 关于原点对称,
关于原点对称, 由
由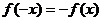 对
对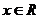 恒成立有
恒成立有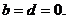 则
则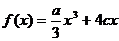 , 又
, 又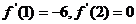 ,
,
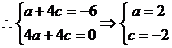 故
故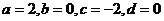
 ……6分
……6分
(2)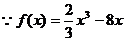 ,
,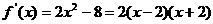
当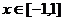 时,
时,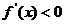 ,
,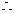
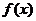 在[-1,1]上递减,而
在[-1,1]上递减,而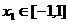
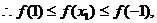 即
即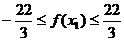
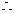
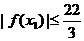 同理,
同理,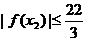
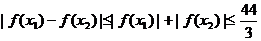 ,故
,故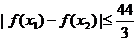 .…………12分
.…………12分
22.解:(1)∵f(x)=3x2+1,g(x)=2x,f(an+1)-f(an)=g(an+1+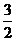 )
)
∴3(an+1)2+1-3a2n-1=2(an+1+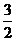 ),即6an=2an+1
),即6an=2an+1
∴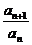 =3 ∴数列{an}是以3为公比的等比等列…………3分
=3 ∴数列{an}是以3为公比的等比等列…………3分
(2)∵bn=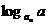 ∴
∴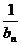 =
=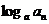 ,
,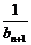 =
=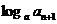
∴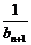 -
-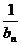 =
=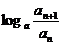 =
=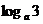
∴数列{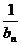 }是以
}是以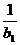 为首项,公差为
为首项,公差为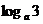 的等差数列…………6分
的等差数列…………6分
(3)为方便起见,记数列{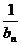 }的公差为
}的公差为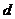 ,由于
,由于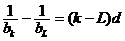 .
.
又∵bk= ,bL=
,bL=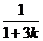
∴
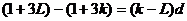 , ∴
, ∴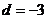
∴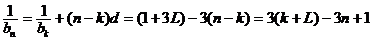
∵k+L=5 ∴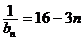
∴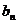 =
=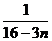 …………10分
…………10分
(4)若k +L =M0,由(3)可知
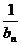 =
=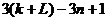 =3M0-3n+1
=3M0-3n+1
假设第M+1项开始满足an>1恒成立,
∵bn=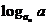 (
(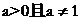 ,n∈N*)
∴
,n∈N*)
∴
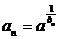
由(3)知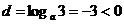 ,∴0<a<1,所以要an>1恒成立,只需
,∴0<a<1,所以要an>1恒成立,只需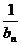 <0,即
<0,即
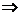

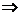
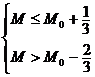
又M∈N*
∴M=M0,即数列{an}从第M0+1项开始以后的项满足a n>1…14分