
网址:http://www.1010jiajiao.com/paper/timu/5159437.html[举报]
12、已知AB是椭圆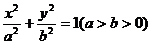 的长轴,若把该长轴
的长轴,若把该长轴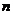 等分,过每个等分点作AB的垂线,依次交椭圆的上半部分于点
等分,过每个等分点作AB的垂线,依次交椭圆的上半部分于点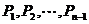 ,设左焦点为
,设左焦点为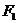 ,
,
则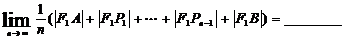
[解]
参考答案
一、填空题:
1、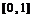 2、3 3、3 4、
2、3 3、3 4、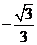 5、 3, -5 6、
5、 3, -5 6、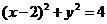
7、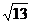 8、
8、 9、
9、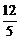 10、
10、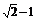 11、①③ 12、
11、①③ 12、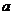
二、选择题(4×4’=16’)
13、C 14、D 15、A 16、 B
三、解答题:
17、[解] :(1)f(x)=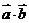 =−cos2x+
=−cos2x+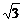 sinxcosx
…………………2分
sinxcosx
…………………2分
=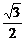 sin2x−
sin2x−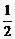 cos2x−
cos2x−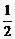 …………………………4分
…………………………4分
=sin(2x−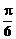 )−
)−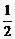 …………………………6分
…………………………6分
∵x∈[0,π],∴当x=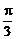 时,f(x)max=1−
时,f(x)max=1−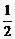 =
=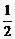 ………8分
………8分
(2)此时x=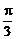 ,设向量
,设向量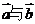 夹角为
夹角为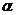 则cos
则cos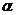 =
=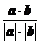 …………9分
…………9分
=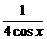 =
=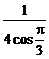 =
=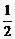 …………………………11分
…………………………11分
所以
向量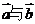 夹角为
夹角为 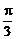 ………………12分
………………12分
18、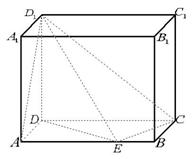 [解]:(1)
[解]:(1)
解法1:由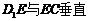
 DE与CE垂直-----1分
DE与CE垂直-----1分
设AE=x,在直角三角形DEC中求得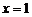 -----2分
-----2分
所以点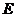 是AB的中点--------------3分
是AB的中点--------------3分
取CD的中点Q,则AQ平行与EC,所以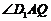 是所求的角------4分
是所求的角------4分
求解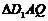 得
得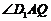 =
=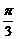 -------------5分
-------------5分
异面直线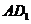 与EC所成的角为
与EC所成的角为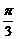 -------6分
-------6分
解法2:利用向量法
分别以DA,DC,D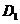 所在的直线为X轴建立坐标系---------------------------------1分
所在的直线为X轴建立坐标系---------------------------------1分
设AE=x,
根据直线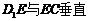

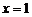 -----2分
-----2分
所以点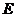 是AB的中点--------------3分
是AB的中点--------------3分
写出A(1,0,0) E(1,1,0 ) C (0,2,0)
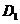 (0,0,1)---------4分
(0,0,1)---------4分
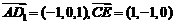
设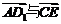 的夹角为
的夹角为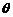 cos
cos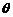 =
=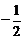 ----------------5分
----------------5分
异面直线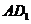 与
与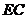 所成的角为
所成的角为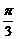 -----------6分
-----------6分
(2)解法1:由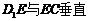
 DE与CE垂直,
DE与CE垂直,
所以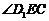 是所求
是所求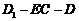 的平面角---8分
的平面角---8分
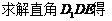
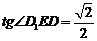 -------11分
-------11分
二面角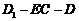 是
是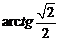 --------12分
--------12分
解法2:利用向量法求得二面角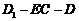 是
是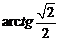
19、[解]:(1)当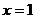 时,
时,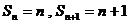 ,
,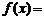
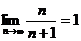 ;…………2分
;…………2分
当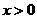 且
且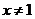 时,
时,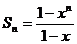 ,
, ,……………………4分
,……………………4分
若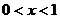 ,
,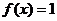 ;……………5分,若
;……………5分,若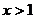 ,则
,则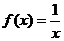 ,……………6分
,……………6分
综上,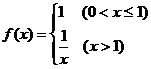 ……………………7分
……………………7分
(2)当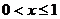 时,由
时,由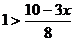 ,得
,得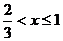 ;……………………10分
;……………………10分
当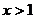 时,由
时,由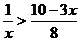 ,得
,得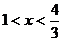 或
或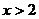 。………………13分
。………………13分
综上可得原不等式的解集为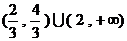 。…………………14分
。…………………14分
20、[解]:设通话x分钟时,方案A,B的通话费分别为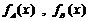 ---------1分
---------1分
(1)当x=120时  =116元
=116元
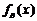 =168元-----------3分
=168元-----------3分
若通话时间为两小时,方案A付话费116元,方案B付话费168元------4分
(2)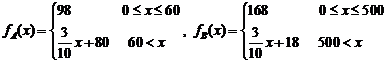 ----------7分
----------7分
当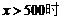
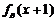 -
-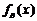 =0.3 --------------------------------9分
=0.3 --------------------------------9分
方案B从500分钟以后,每分钟收费0.3 元-------------------10分
(3) 当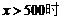
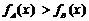 -------------------------------11分
-------------------------------11分
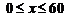
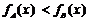 ----------------------12分
----------------------12分
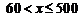 由
由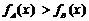 得
得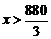 ----------13分
----------13分
综合:通话时间在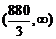 内方案B较优惠。----------14分
内方案B较优惠。----------14分
21、[解]:(1)由于点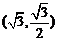 在椭圆上,
在椭圆上,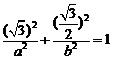 ------1分
------1分
2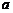 =4,
------2分
=4,
------2分
椭圆C的方程为 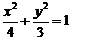 --------3分
--------3分
焦点坐标分别为(-1,0) ,(1,0)-----------4分
(2)设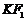 的中点为B(x, y)则点
的中点为B(x, y)则点 --------6分
--------6分
把K的坐标代入椭圆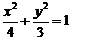 中得
中得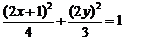 -----8分
-----8分
线段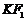 的中点B的轨迹方程为
的中点B的轨迹方程为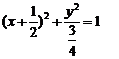 ----------10分
----------10分
(3)过原点的直线L与椭圆相交的两点M,N关于坐标原点对称
设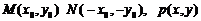 ----11分
----11分
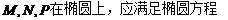 ,得
,得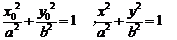 ------12分
------12分
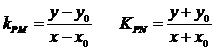 -------------------13分
-------------------13分
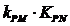 =
=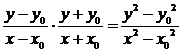 =
=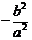 -----------15分
-----------15分
故: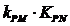 的值与点P的位置无关,同时与直线L无关,-----16分
的值与点P的位置无关,同时与直线L无关,-----16分
22、 [解]:(1)当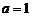 时,
时,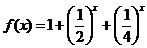
因为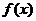 在
在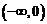 上递减,所以
上递减,所以 ,即
,即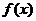 在
在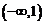 的值域为
的值域为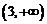
故不存在常数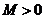 ,使
,使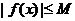 成立
成立
所以函数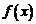 在
在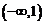 上不是有界函数。
……………4分(没有判断过程,扣2分)
上不是有界函数。
……………4分(没有判断过程,扣2分)
(2)由题意知,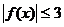 在
在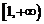 上恒成立。………5分
上恒成立。………5分
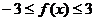 ,
, 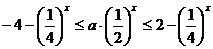
∴ 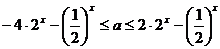 在
在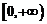 上恒成立………6分
上恒成立………6分
∴ 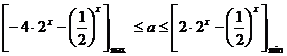 ………7分
………7分
设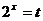 ,
,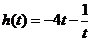 ,
,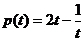 ,由
,由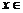
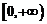 得 t≥1,
得 t≥1,
设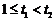 ,
,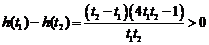
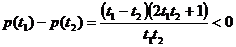
所以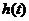 在
在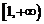 上递减,
上递减,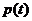 在
在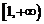 上递增,………9分(单调性不证,不扣分)
上递增,………9分(单调性不证,不扣分)
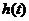 在
在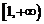 上的最大值为
上的最大值为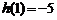 ,
, 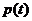 在
在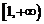 上的最小值为
上的最小值为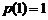
所以实数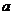 的取值范围为
的取值范围为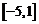 。…………………………………11分
。…………………………………11分
(3)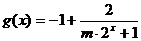 ,
,
∵
m>0 ,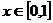 ∴
∴ 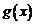 在
在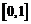 上递减,………12分
上递减,………12分
∴
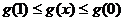 即
即 ………13分
………13分
①当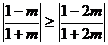 ,即
,即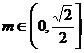 时,
时,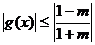 , ………14分
, ………14分
此时  ,………16分
,………16分
②当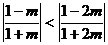 ,即
,即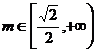 时,
时,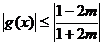 ,
,
此时 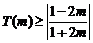 , ---------17分
, ---------17分
综上所述,当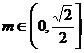 时,
时,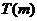 的取值范围是
的取值范围是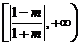 ;
;
当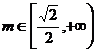 时,
时,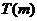 的取值范围是
的取值范围是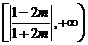 ………18
………18