
网址:http://www.1010jiajiao.com/paper/timu/5159569.html[举报]
5.()已知x,y,z∈R,且x+y+z=1,x2+y2+z2=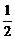 ,证明:x,y,z∈[0,
,证明:x,y,z∈[0,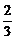 ]
]
参考答案
难点磁场
证法一:(分析综合法)
欲证原式,即证4(ab)2+4(a2+b2)-25ab+4≥0,即证4(ab)2-33(ab)+8≥0,即证ab≤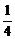 或ab≥8.
或ab≥8.
∵a>0,b>0,a+b=1,∴ab≥8不可能成立
∵1=a+b≥2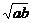 ,∴ab≤
,∴ab≤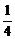 ,从而得证.
,从而得证.
证法二:(均值代换法)
设a=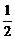 +t1,b=
+t1,b=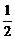 +t2.
+t2.
∵a+b=1,a>0,b>0,∴t1+t2=0,|t1|<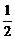 ,|t2|<
,|t2|<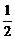
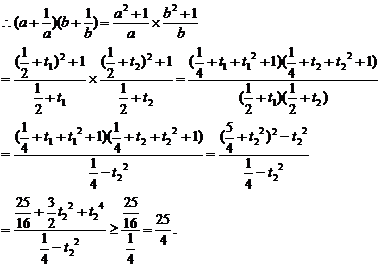
显然当且仅当t=0,即a=b=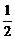 时,等号成立.
时,等号成立.
证法三:(比较法)
∵a+b=1,a>0,b>0,∴a+b≥2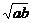 ,∴ab≤
,∴ab≤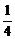
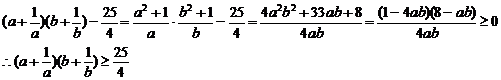
证法四:(综合法)
∵a+b=1, a>0,b>0,∴a+b≥2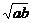 ,∴ab≤
,∴ab≤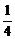 .
.
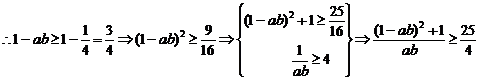

证法五:(三角代换法)
∵ a>0,b>0,a+b=1,故令a=sin2α,b=cos2α,α∈(0,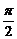 )
)
 2
2
歼灭难点训练
一、1.解析:令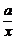 =cos2θ,
=cos2θ,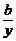 =sin2θ,则x=asec2θ,y=bcsc2θ,∴x+y=asec2θ+bcsc2θ=a+b+atan2θ+bcot2θ≥a+b+2
=sin2θ,则x=asec2θ,y=bcsc2θ,∴x+y=asec2θ+bcsc2θ=a+b+atan2θ+bcot2θ≥a+b+2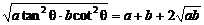 .
.
答案:a+b+2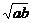
2.解析:由0≤|a-d|<|b-c|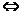 (a-d)2<(b-c)2
(a-d)2<(b-c)2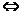 (a+b)2-4ad<(b+c)2-4bc
(a+b)2-4ad<(b+c)2-4bc
∵a+d=b+c,∴-4ad<-4bc,故ad>bc.
答案:ad>bc
3.解析:把p、q看成变量,则m<p<n,m<q<n.
答案:m<p<q<n
二、4.(1)证法一:a2+b2+c2- =
= (3a2+3b2+3c2-1)
(3a2+3b2+3c2-1)
= [3a2+3b2+3c2-(a+b+c)2]
[3a2+3b2+3c2-(a+b+c)2]
= [3a2+3b2+3c2-a2-b2-c2-2ab-2ac-2bc]
[3a2+3b2+3c2-a2-b2-c2-2ab-2ac-2bc]
= [(a-b)2+(b-c)2+(c-a)2]≥0 ∴a2+b2+c2≥
[(a-b)2+(b-c)2+(c-a)2]≥0 ∴a2+b2+c2≥
证法二:∵(a+b+c)2=a2+b2+c2+2ab+2ac+2bc≤a2+b2+c2+a2+b2+a2+c2+b2+c2
∴3(a2+b2+c2)≥(a+b+c)2=1
∴a2+b2+c2≥
证法三:∵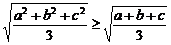 ∴a2+b2+c2≥
∴a2+b2+c2≥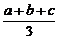
∴a2+b2+c2≥
证法四:设a= +α,b=
+α,b= +β,c=
+β,c= +γ.
+γ.
∵a+b+c=1,∴α+β+γ=0
∴a2+b2+c2=( +α)2+(
+α)2+( +β)2+(
+β)2+( +γ)2
+γ)2
= +
+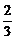 (α+β+γ)+α2+β2+γ2
(α+β+γ)+α2+β2+γ2
= +α2+β2+γ2≥
+α2+β2+γ2≥
∴a2+b2+c2≥
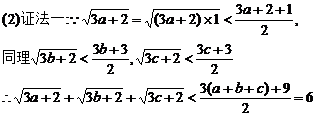
∴原不等式成立.
证法二: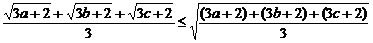
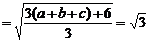
∴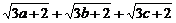 ≤
≤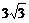 <6
<6
∴原不等式成立.
5.证法一:由x+y+z=1,x2+y2+z2=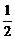 ,得x2+y2+(1-x-y)2=
,得x2+y2+(1-x-y)2=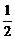 ,整理成关于y的一元二次方程得:
,整理成关于y的一元二次方程得:
2y2-2(1-x)y+2x2-2x+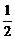 =0,∵y∈R,故Δ≥0
=0,∵y∈R,故Δ≥0
∴4(1-x)2-4×2(2x2-2x+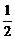 )≥0,得0≤x≤
)≥0,得0≤x≤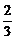 ,∴x∈[0,
,∴x∈[0,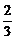 ]
]
同理可得y,z∈[0,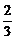 ]
]
证法二:设x= +x′,y=
+x′,y= +y′,z=
+y′,z= +z′,则x′+y′+z′=0,
+z′,则x′+y′+z′=0,
于是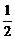 =(
=( +x′)2+(
+x′)2+( +y′)2+(
+y′)2+( +z′)2
+z′)2
= +x′2+y′2+z′2+
+x′2+y′2+z′2+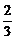 (x′+y′+z′)
(x′+y′+z′)
= +x′2+y′2+z′2≥
+x′2+y′2+z′2≥ +x′2+
+x′2+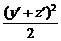 =
= +
+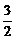 x′2
x′2
故x′2≤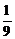 ,x′∈[-
,x′∈[- ,
, ],x∈[0,
],x∈[0,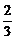 ],同理y,z∈[0,
],同理y,z∈[0,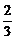 ]
]
证法三:设x、y、z三数中若有负数,不妨设x<0,则x2>0,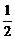 =x2+y2+z2≥x2+
=x2+y2+z2≥x2+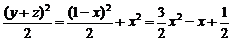 >
>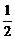 ,矛盾.
,矛盾.
x、y、z三数中若有最大者大于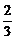 ,不妨设x>
,不妨设x>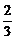 ,则
,则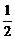 =x2+y2+z2≥x2+
=x2+y2+z2≥x2+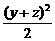 =x2+
=x2+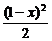 =
=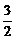 x2-x+
x2-x+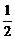
=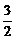 x(x-
x(x-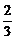 )+
)+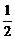 >
>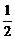 ;矛盾.
;矛盾.
故x、y、z∈[0,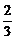 ]
]
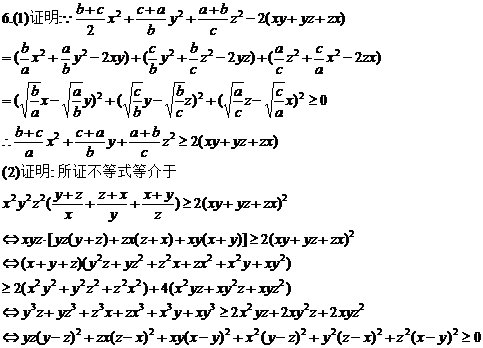
∵上式显然成立,∴原不等式得证.
7.证明:(1)对于1<i≤m,且A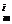 =m.….(m-i+1),
=m.….(m-i+1),
 ,
,
由于m<n,对于整数k=1,2,…,i-1,有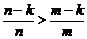 ,
,
所以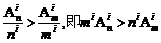
(2)由二项式定理有:
(1+m)n=1+C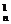 m+C
m+C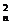 m2+…+C
m2+…+C mn,
mn,
(1+n)m=1+C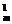 n+C
n+C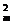 n2+…+C
n2+…+C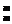 nm,
nm,
由(1)知miA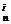 >niA
>niA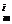 (1<i≤m
(1<i≤m
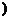 ,而C
,而C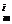 =
=
∴miCin>niCim(1<m<n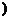
∴m0C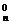 =n0C
=n0C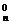 =1,mC
=1,mC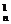 =nC
=nC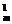 =m.n,m2C
=m.n,m2C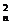 >n2C
>n2C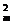 ,…,
,…,
mmC >nmC
>nmC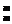 ,mm+1C
,mm+1C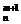 >0,…,mnC
>0,…,mnC >0,
>0,
∴1+C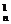 m+C
m+C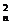 m2+…+C
m2+…+C mn>1+C
mn>1+C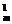 n+C2mn2+…+C
n+C2mn2+…+C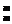 nm,
nm,
即(1+m)n>(1+n)m成立.
8.证法一:因a>0,b>0,a3+b3=2,所以
(a+b)3-23=a3+b3+3a2b+3ab2-8=3a2b+3ab2-6
=3[ab(a+b)-2]=3[ab(a+b)-(a3+b3)]=-3(a+b)(a-b)2≤0.
即(a+b)3≤23,又a+b>0,所以a+b≤2,因为2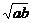 ≤a+b≤2,
≤a+b≤2,
所以ab≤1.
证法二:设a、b为方程x2-mx+n=0的两根,则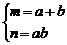 ,
,
因为a>0,b>0,所以m>0,n>0,且Δ=m2-4n≥0 ①
因为2=a3+b3=(a+b)(a2-ab+b2)=(a+b)[(a+b)2-3ab]=m(m2-3n)
所以n=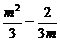 ②
②
将②代入①得m2-4(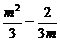 )≥0,
)≥0,
即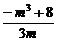 ≥0,所以-m3+8≥0,即m≤2,所以a+b≤2,
≥0,所以-m3+8≥0,即m≤2,所以a+b≤2,
由2≥m 得4≥m2,又m2≥4n,所以4≥4n,
即n≤1,所以ab≤1.
证法三:因a>0,b>0,a3+b3=2,所以
2=a3+b3=(a+b)(a2+b2-ab)≥(a+b)(2ab-ab)=ab(a+b)
于是有6≥3ab(a+b),从而8≥3ab(a+b)+2=3a2b+3ab2+a3+b3=
(a+b)3,所以a+b≤2,(下略)
证法四:因为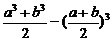
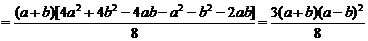 ≥0,
≥0,
所以对任意非负实数a、b,有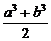 ≥
≥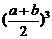
因为a>0,b>0,a3+b3=2,所以1=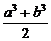 ≥
≥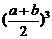 ,
,
∴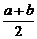 ≤1,即a+b≤2,(以下略)
≤1,即a+b≤2,(以下略)
证法五:假设a+b>2,则
a3+b3=(a+b)(a2-ab+b2)=(a+b)[(a+b)2-3ab]>(a+b)ab>2ab,所以ab<1,
又a3+b3=(a+b)[a2-ab+b2]=(a+b)[(a+b)2-3ab]>2(22-3ab)
因为a3+b3=2,所以2>2(4-3ab),因此ab>1,前后矛盾,故a+b≤2(以下略)