
网址:http://www.1010jiajiao.com/paper/timu/5159573.html[举报]
1.()定义在R上的奇函数f(x)为增函数,偶函数g(x)在区间[0,+∞)的图象与f(x)的图象重合,设a>b>0,给出下列不等式,其中正确不等式的序号是( )
①f(b)-f(-a)>g(a)-g(-b) ②f(b)-f(-a)<g(a)-g(-b)
③f(a)-f(-b)>g(b)-g(-a) ④f(a)-f(-b)<g(b)-g(-a)
A.①③ B.②④ C.①④ D.②③
参考答案
难点磁场
解:(1)令F(x)=f(x)-x,因为x1,x2是方程f(x)-x=0的根,所以F(x)=a(x-x1)(x-x2).当x∈(0,x1)时,由于x1<x2,得(x-x1)(x-x2)>0,
又a>0,得F(x)=a(x-x1)(x-x2)>0,即x<f(x)
x1-f(x)=x1-[x+F(x)]=x1-x+a(x1-x)(x-x2)=(x1-x)[1+a(x-x2)]
∵0<x<x1<x2<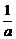 ,∴x1-x>0,1+a(x-x2)=1+ax-ax2>1-ax2>0
,∴x1-x>0,1+a(x-x2)=1+ax-ax2>1-ax2>0
∴x1-f(x)>0,由此得f(x)<x1.
(2)依题意:x0=-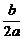 ,因为x1、x2是方程f(x)-x=0的两根,即x1,x2是方程ax2+(b-1)x+c=0的根.
,因为x1、x2是方程f(x)-x=0的两根,即x1,x2是方程ax2+(b-1)x+c=0的根.
∴x1+x2=-
∴x0=-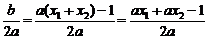 ,因为ax2<1,
,因为ax2<1,
∴x0<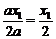
歼灭难点训练
一、1.解析:由题意f(a)=g(a)>0,f(b)=g(b)>0,且f(a)>f(b),g(a)>g(b)
∴f(b)-f(-a)=f(b)+f(a)=g(a)+g(b)
而g(a)-g(-b)=g(a)-g(b)∴g(a)+g(b)-[g(a)-g(b)]
=2g(b)>0,∴f(b)-f(-a)>g(a)-g(-b)
同理可证:f(a)-f(-b)>g(b)-g(-a)
答案:A
二、2.解析:①②③不满足均值不等式的使用条件“正、定、等”.④式:|x-y|=|(x-2)-(y-2)|≤|(x-2)-(y-2)|≤|x-2|+|y-2|<ε+ε=2ε.
答案:④
3.解析:由已知y1= ;y2=0.8x(x为仓库与车站距离)费用之和y=y1+y2=0.8x+
;y2=0.8x(x为仓库与车站距离)费用之和y=y1+y2=0.8x+  ≥2
≥2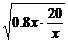 =8
=8
当且仅当0.8x= 即x=5时“=”成立
即x=5时“=”成立
答案:5公里处
三、4.证明:(1)设g(x)=f(x)-x=ax2+(b-1)x+1,且x>0.
∵x1<2<x2<4,∴(x1-2)(x2-2)<0,即x1x2<2(x1+x2)-4,
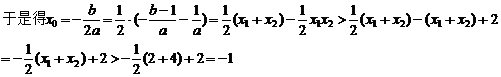
(2)解:由方程g(x)=ax2+(b-1)x+1=0可知x1.x2=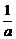 >0,所以x1,x2同号
>0,所以x1,x2同号
1°若0<x1<2,则x2-x1=2,∴x2=x1+2>2,
∴g(2)<0,即4a+2b-1<0 ①
又(x2-x1)2=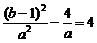
∴2a+1= (∵a>0)代入①式得,
(∵a>0)代入①式得,
2 <3-2b ②
<3-2b ②
解②得b<
2°若 -2<x1<0,则x2=-2+x1<-2
∴g(-2)<0,即4a-2b+3<0 ③
又2a+1= ,代入③式得
,代入③式得
2 <2b-1 ④
<2b-1 ④
解④得b>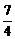 .
.
综上,当0<x1<2时,b< ,当-2<x1<0时,b>
,当-2<x1<0时,b>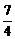 .
.
5.解:(1)由题意知某商品定价上涨x成时,上涨后的定价、每月卖出数量、每月售货金额分别是:p(1+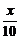 )元、n(1-
)元、n(1-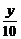 )元、npz元,因而
)元、npz元,因而
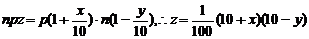 ,在y=ax的条件下,z=
,在y=ax的条件下,z=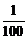 [-a
[-a
[x-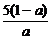 ]2+100+
]2+100+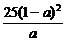 ].由于
].由于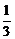 ≤a<1,则0<
≤a<1,则0<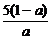 ≤10.
≤10.
要使售货金额最大,即使z值最大,此时x=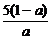 .
.
(2)由z=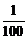 (10+x)(10-
(10+x)(10-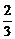 x)>1,解得0<x<5.
x)>1,解得0<x<5.
6.(1)证明:令m>0,n=0得:f(m)=f(m).f(0).∵f(m)≠0,∴f(0)=1
取m=m,n=-m,(m<0),得f(0)=f(m)f(-m)
∴f(m)=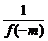 ,∵m<0,∴-m>0,∴0<f(-m)<1,∴f(m)>1
,∵m<0,∴-m>0,∴0<f(-m)<1,∴f(m)>1
(2)证明:任取x1,x2∈R,则f(x1)-f(x2)=f(x1)-f[(x2-x1)+x1]
=f(x1)-f(x2-x1).f(x1)=f(x1)[1-f(x2-x1)],
∵f(x1)>0,1-f(x2-x1)>0,∴f(x1)>f(x2),
∴函数f(x)在R上为单调减函数.
(3)由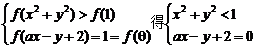 ,由题意此不等式组无解,数形结合得:
,由题意此不等式组无解,数形结合得: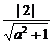 ≥1,解得a2≤3
≥1,解得a2≤3
∴a∈[-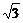 ,
,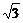 ]
]
7.(1)解:设y=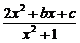 ,则(y-2)x2-bx+y-c=0 ①
,则(y-2)x2-bx+y-c=0 ①
∵x∈R,∴①的判别式Δ≥0,即 b2-4(y-2)(y-c)≥0,
即4y2-4(2+c)y+8c+b2≤0 ②
由条件知,不等式②的解集是[1,3]
∴1,3是方程4y2-4(2+c)y+8c+b2=0的两根
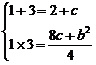 ∴c=2,b=-2,b=2(舍)
∴c=2,b=-2,b=2(舍)
(2)任取x1,x2∈[-1,1],且x2>x1,则x2-x1>0,且
(x2-x1)(1-x1x2)>0,∴f(x2)-f(x1)=-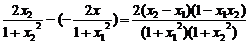 >0,
>0,
∴f(x2)>f(x1),lgf(x2)>lgf(x1),即F(x2)>F(x1)
∴F(x)为增函数.
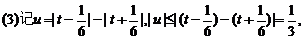
即-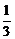 ≤u≤
≤u≤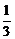 ,根据F(x)的单调性知
,根据F(x)的单调性知
F(-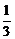 )≤F(u)≤F(
)≤F(u)≤F(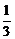 ),∴lg
),∴lg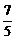 ≤F(|t-
≤F(|t-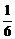 |-|t+
|-|t+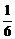 |)≤lg
|)≤lg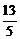 对任意实数t 成立.
对任意实数t 成立.