
网址:http://www.1010jiajiao.com/paper/timu/5159588.html[举报]
4.()已知圆内接四边形ABCD的边长分别为AB=2,BC=6,CD=DA=4,求四边形ABCD的面积.
参考答案
难点磁场
解法一:由题设条件知B=60°,A+C=120°.
设α=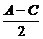 ,则A-C=2α,可得A=60°+α,C=60°-α,
,则A-C=2α,可得A=60°+α,C=60°-α,
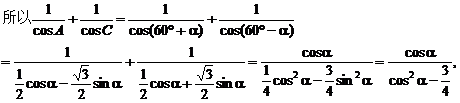
依题设条件有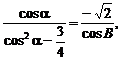
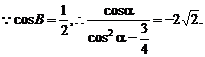
整理得4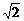 cos2α+2cosα-3
cos2α+2cosα-3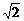 =0(M)
=0(M)
(2cosα-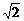 )(2
)(2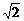 cosα+3)=0,∵2
cosα+3)=0,∵2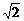 cosα+3≠0,
cosα+3≠0,
∴2cosα-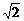 =0.从而得cos
=0.从而得cos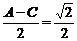 .
.
解法二:由题设条件知B=60°,A+C=120°
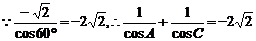 ①,把①式化为cosA+cosC=-2
①,把①式化为cosA+cosC=-2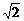 cosAcosC ②,
cosAcosC ②,
利用和差化积及积化和差公式,②式可化为
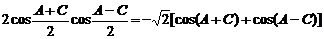 ③,
③,
将cos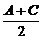 =cos60°=
=cos60°= ,cos(A+C)=-
,cos(A+C)=- 代入③式得:
代入③式得:
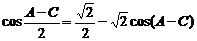 ④
④
将cos(A-C)=2cos2(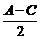 )-1代入 ④:4
)-1代入 ④:4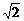 cos2(
cos2(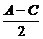 )+2cos
)+2cos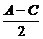 -3
-3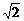 =0,(*),
=0,(*),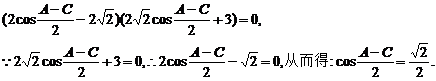
歼灭难点训练
一、1.解析:其中(3)(4)正确.
答案: B
二、2.解析:∵A+B+C=π,A+C=2B,
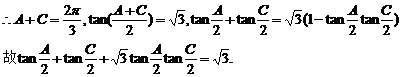
答案: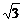
3.解析:∵A为最小角∴2A+C=A+A+C<A+B+C=180°.
∵cos(2A+C)=-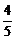 ,∴sin(2A+C)=
,∴sin(2A+C)=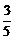 .
.
∵C为最大角,∴B为锐角,又sinB=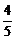 .故cosB=
.故cosB=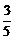 .
.
即sin(A+C)=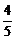 ,cos(A+C)=-
,cos(A+C)=-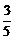 .
.
∵cos(B+C)=-cosA=-cos[(2A+C)-(A+C)]=-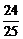 ,
,
∴cos2(B+C)=2cos2(B+C)-1=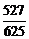 .
.
答案: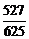
三、4.解:如图:连结BD,则有四边形ABCD的面积:
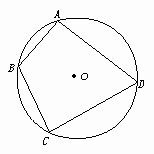
S=S△ABD+S△CDB= .AB.ADsinA+
.AB.ADsinA+ .BC.CD.sinC
.BC.CD.sinC
∵A+C=180°,∴sinA=sinC
故S= (AB.AD+BC.CD)sinA=
(AB.AD+BC.CD)sinA= (2×4+6×4)sinA=16sinA
(2×4+6×4)sinA=16sinA
由余弦定理,在△ABD中,BD2=AB2+AD2-2AB.AD.cosA=20-16cosA
在△CDB中,BD2=CB2+CD2-2CB.CD.cosC=52-48cosC
∴20-16cosA=52-48cosC,∵cosC=-cosA,
∴64cosA=-32,cosA=- ,又0°<A<180°,∴A=120°故S=16sin120°=8
,又0°<A<180°,∴A=120°故S=16sin120°=8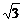 .
.
5.解:R=rcosθ,由此得: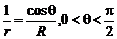 ,
,
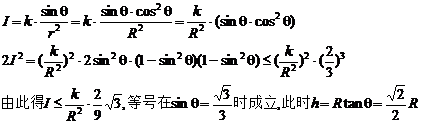
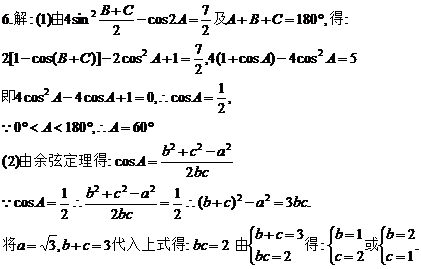
7.解:由a、b、3c成等比数列,得:b2=3ac
∴sin2B=3sinC.sinA=3(- )[cos(A+C)-cos(A-C)]
)[cos(A+C)-cos(A-C)]
∵B=π-(A+C).∴sin2(A+C)=-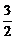 [cos(A+C)-cos
[cos(A+C)-cos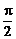 ]
]
即1-cos2(A+C)=-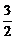 cos(A+C),解得cos(A+C)=-
cos(A+C),解得cos(A+C)=- .
.
∵0<A+C<π,∴A+C=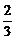 π.又A-C=
π.又A-C=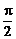 ∴A=
∴A=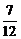 π,B=
π,B=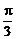 ,C=
,C=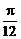 .
.
8.解:按题意,设折叠后A点落在边BC上改称P点,显然A、P两点关于折线DE对称,又设∠BAP=θ,∴∠DPA=θ,∠BDP=2θ,再设AB=a,AD=x,∴DP=x.在△ABC中,
∠APB=180°-∠ABP-∠BAP=120°-θ,
由正弦定理知: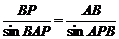 .∴BP=
.∴BP=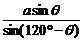
在△PBD中,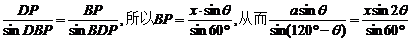 ,
,
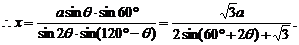
∵0°≤θ≤60°,∴60°≤60°+2θ≤180°,∴当60°+2θ=90°,即θ=15°时,
sin(60°+2θ)=1,此时x取得最小值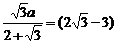 a,即AD最小,∴AD∶DB=2
a,即AD最小,∴AD∶DB=2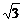 -3.
-3.