
网址:http://www.1010jiajiao.com/paper/timu/5159673.html[举报]
11.若复数Z满足关系式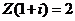 ,则Z的共轭复数为
,则Z的共轭复数为
参考答案
一、选择题:
|
题号 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
答案 |
C |
B |
B |
C |
A |
C |
D |
B |
C |
C |
二、填空题:
11、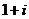 12、560 13、
12、560 13、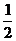 14、
14、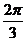 15、充分非必要
15、充分非必要 
三、解答题:
16、(1)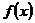

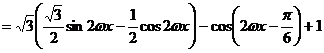
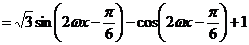 (2分)
(2分)
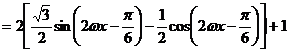
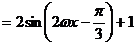 (6分)
(6分)

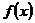 值域为
值域为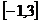 (不同变形参照给分)
(不同变形参照给分)
(2)因为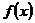 周期为
周期为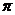

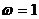 (8分)
(8分)
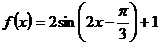
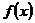 在
在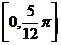 、
、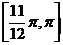 上单调递增,在
上单调递增,在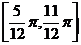 上单调递减。
上单调递减。
(12分)
17、(1)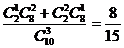 (4分)
(4分)
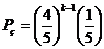
(2)分布列为:
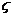 |
1 |
2 |
3 |
… |
 |
… |
 |
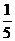 |
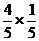 |
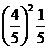 |
… |
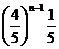 |
… |
(7分 没写后面省略号扣1分)
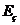
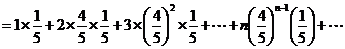
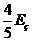
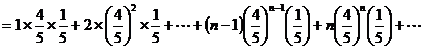

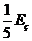
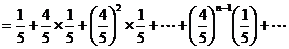
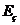
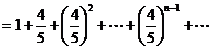
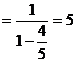
(12分 直接用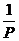 计算只给2分)
计算只给2分)
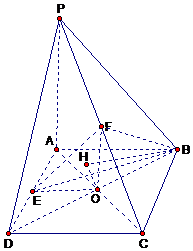
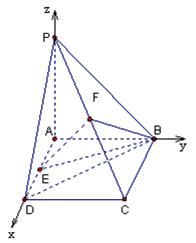 18、方法一:
18、方法一:
设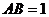 ,则
,则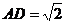
(1)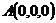
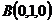
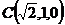
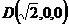
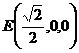
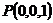
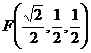
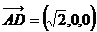
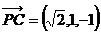
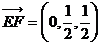

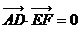


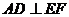
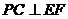
故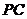 为
为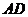 及
及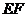 的公垂线
(6分)
的公垂线
(6分)
(2)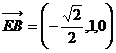
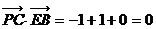

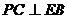

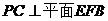 故
故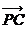 可看成平面
可看成平面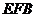 的法向量
的法向量
 故
故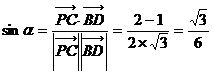 (12分)
(12分)
方法二:
(1)连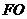 、
、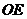 、
、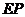 、
、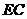
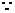
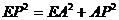
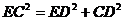
又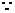
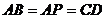
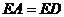

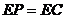
又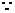
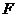 为
为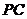 的中点
的中点

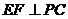
又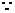
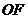 ∥
∥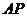

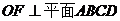
而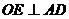

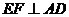
故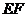 为
为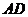 及
及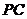 的公垂线
(6分)
的公垂线
(6分)
(2)过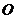 作
作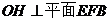 于
于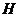 ,连
,连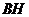 ,
,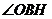 为所求
为所求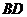 与平面
与平面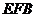 所成的角
(8分)
所成的角
(8分)
设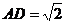
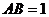
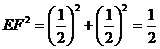
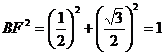

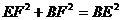

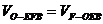
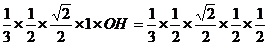 (10分)
(10分)

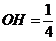
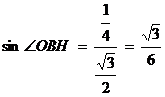 (12分)
(12分)
(其它解法参照给分)
19、(1)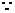
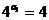

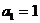
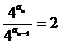

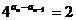
即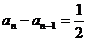 故
故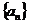 是以1为首项,
是以1为首项,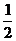 为公差的等差数列 (3分)
为公差的等差数列 (3分)

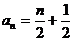
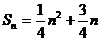 (5分)
(5分)
(2)设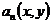

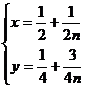
由此可得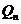 在直线
在直线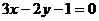 上
(8分)
上
(8分)
横坐标、纵坐标随 的增大而减小,并与
的增大而减小,并与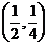 无限接近,故所求圆就是以
无限接近,故所求圆就是以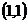 、
、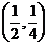 为直径端点的圆
为直径端点的圆
即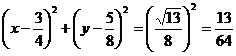 (12分)
(12分)
20、(1)由题知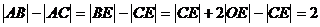
根据双曲线定义知,点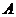 的轨迹是以
的轨迹是以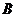 、
、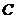 为焦点,实轴长为2的双曲线的右支除去点
为焦点,实轴长为2的双曲线的右支除去点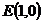 ,故
,故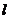 的方程为
的方程为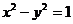 (
(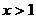 ) (5分)
) (5分)
(2)设点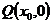 、
、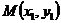 、
、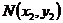 ,由(1)可知
,由(1)可知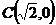
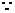
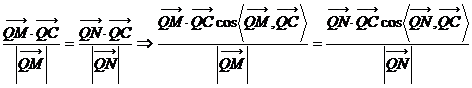

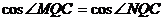

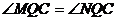 (7分)
(7分)
①当直线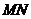
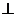
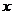 轴时,点
轴时,点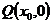 在
在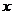 轴上任何一点处都能使得
轴上任何一点处都能使得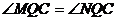 成立
成立
②当直线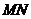 不与
不与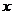 轴垂直时,设直线
轴垂直时,设直线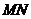 :
: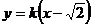
由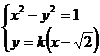 得
得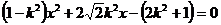

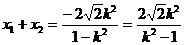
 (9分)
(9分)

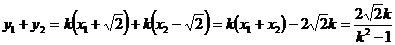
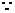

要使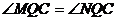 ,只需
,只需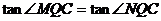 成立
成立
即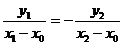 即
即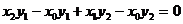 (11分)
(11分)

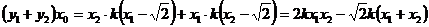
即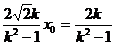 故
故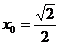
故所求的点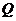 的坐标为
的坐标为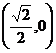 时,使
时,使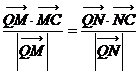 成立
成立
(13分)
21、(1)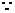
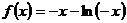
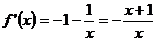
 当
当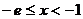 时,
时,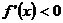 ,此时
,此时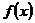 为单调递减
为单调递减
当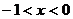 时,
时,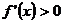 ,此时
,此时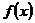 为单调递增
为单调递增

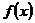 的极小值为
的极小值为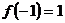 (4分)
(4分)
(2)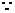
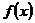 的极小值,即
的极小值,即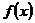 在
在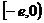 的最小值为1
的最小值为1

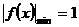 令
令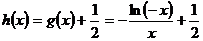
又
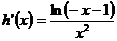 当
当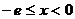 时
时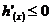
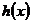 在
在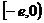 上单调递减
上单调递减

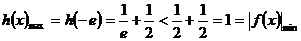 (8分)
(8分)
 当
当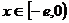 时,
时,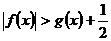
(3)假设存在实数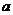 ,使
,使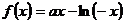 有最小值3,
有最小值3,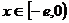
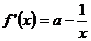
①当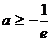 时,由于
时,由于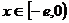 ,则
,则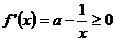
 函数
函数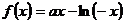 是
是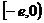 上的增函数
上的增函数

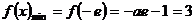
解得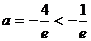 (舍去)
(10分)
(舍去)
(10分)
②当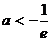 时,则当
时,则当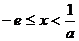 时,
时,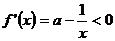
此时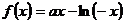 是减函数
是减函数
当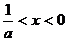 时,
时,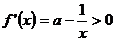 ,此时
,此时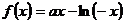 是增函数
是增函数

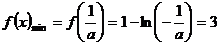
解得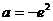 (13分)
(13分)
由①、②知,存在实数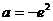 ,使得当
,使得当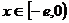 时
时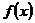 有最小值3
有最小值3
(14分)