
网址:http://www.1010jiajiao.com/paper/timu/5159720.html[举报]
20.(本小题满分12分)
已知各项均为正数的数列{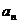 }满足
}满足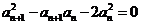 (
(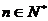 ),且
),且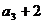 是
是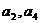 的等差中项.
的等差中项.
(Ⅰ)求数列{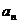 }的通项公式
}的通项公式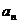 ;
;
(Ⅱ)若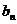 =
=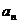
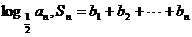 ,求使S
,求使S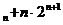 >50成立的正整数n的最小值.
>50成立的正整数n的最小值.
参考答案
一、选择题:
1.C 2.A 3.B 4.B 5.A 6.C 7.D 8.D 9.B 10.A 11.C 12.B
|
13.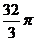 14.(7,3) 15.2
16.7
14.(7,3) 15.2
16.7
17.解:(1) ∵ m n
n , m . n
, m . n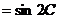 ,
,
∴sinAcosB+cosAsinB=sin2C 1分
即 sinC=sin2C 3分
∴ cosC= 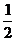 4分
4分
又C为三角形的内角, ∴ 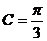 6分
6分
(Ⅱ) ∵sinA,sinC,sinB成等比数列,
∴ sin2C=sinAsinB 7分
∴ c2=ab 8分
又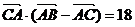 ,即
,即 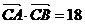 ,
9分
,
9分
∴ abcosC=18 10分
∴ ab=36 故 c2=36
∴ c=6 12分
18.解:(Ⅰ)3个旅游团选择3条不同线路的概率为P1=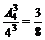 …………3分
…………3分
(Ⅱ)恰有两条线路被选择的概率为P2=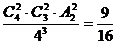 ……6分
……6分
(Ⅲ)设选择甲线路旅游团数为ξ,则ξ=0,1,2,3
P(ξ=0)=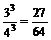 P(ξ=1)=
P(ξ=1)=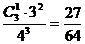
P(ξ=2)= 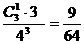 P(ξ=3)=
P(ξ=3)= 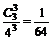 ……………………8分
……………………8分
|
ξ |
0 |
1 |
2 |
3 |
|
P |
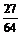 |
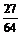 |
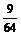 |
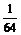
|
∴ξ的分布列为:
∴期望Eξ=0×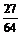 +1×
+1×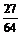 +2×
+2×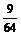 +3×
+3×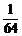 =
=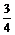 ……………………………12分
……………………………12分
19.方法一
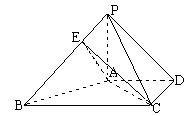
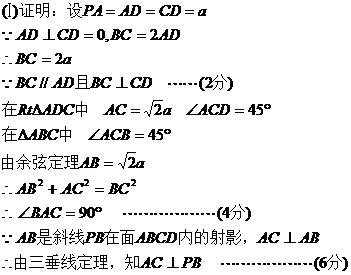
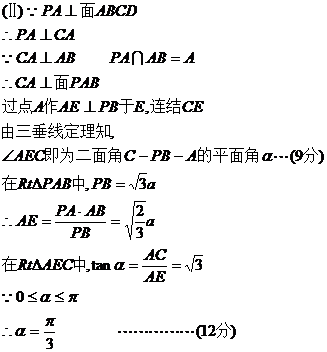
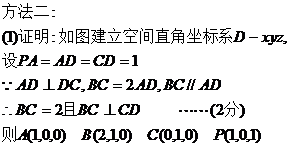
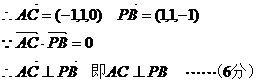
(2)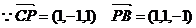

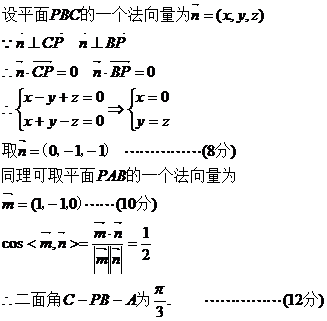
20.解:(Ⅰ)∵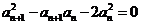 ,
,
∴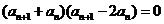 ,
,
∵数列{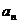 }的各项均为正数,
}的各项均为正数,
∴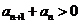 ,
,
∴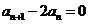 ,
,
即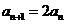 (
(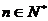 ),所以数列{
),所以数列{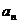 }是以2为公比的等比数列.………………3分
}是以2为公比的等比数列.………………3分
∵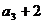 是
是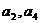 的等差中项,
的等差中项,
∴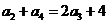 ,
,
∴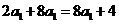 ,∴
,∴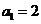 ,
,
∴数列{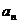 }的通项公式
}的通项公式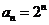 .……………………………………………………6分
.……………………………………………………6分
(Ⅱ)由(Ⅰ)及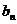 =
=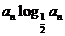 得,
得,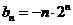 , ……………………………8分
, ……………………………8分
∵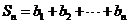 ,
,
∴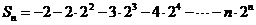 1
1
∴ ②
②
②-1得,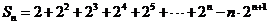
= ……………………………10分
……………………………10分
要使S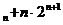 >50成立,只需2n+1-2>50成立,即2n+1>52,n³5
>50成立,只需2n+1-2>50成立,即2n+1>52,n³5
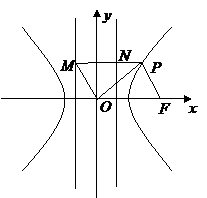 ∴使S
∴使S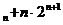 >50成立的正整数n的最小值为5. ……………………………12分
>50成立的正整数n的最小值为5. ……………………………12分
21.解:(Ⅰ)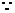
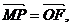
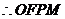 为平行四边形.
为平行四边形.
设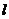 是双曲线的右准线,且与
是双曲线的右准线,且与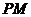 交于
交于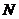 点,
点,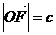 ,
,
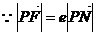 ,
,
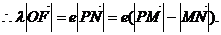
即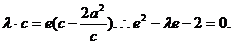 ………………6分
………………6分
(Ⅱ)当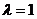 时,得
时,得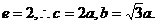
所以可设双曲线的方程是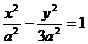 ,…8分
,…8分
设直线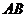 的方程是
的方程是 与双曲线方程联立得:
与双曲线方程联立得: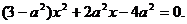
由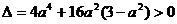 得
得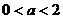 .
.
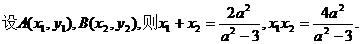 ①
①
由已知,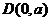 ,因为
,因为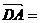
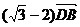 ,
,
所以可得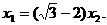 ②…………10分
②…………10分
由①②得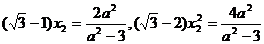 ,
,
消去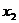 得
得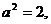 符合
符合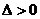 ,
,
所以双曲线的方程是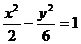 ………………14分
………………14分
22.解:(Ⅰ)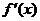 =
=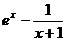 ,………………2分
,………………2分
当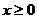 时,
时,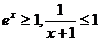 ,所以当
,所以当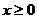 时,
时,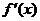
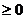 ,
,
则函数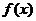 在
在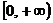 上单调递增,
上单调递增,
所以函数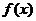 的最小值为
的最小值为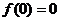 ;………………………………5分
;………………………………5分
(Ⅱ)由(Ⅰ)知,当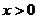 时,
时,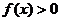 ,∵
,∵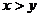 ,
,
∴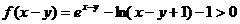 ,
,
∴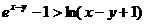 ①……………………7分
①……………………7分
∵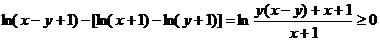 ,
,
∴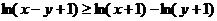 ②…………………………10分
②…………………………10分
由①②得  …………………………………12分
…………………………………12分