
网址:http://www.1010jiajiao.com/paper/timu/5159803.html[举报]
17.已知数列 {2 n•an} 的前 n 项和 Sn = 9-6n.
(I) 求数列 {an} 的通项公式;
(II) 设 bn = n.(2-log 2 ),求数列 { } 的前 n 项和Tn.
08年高考理科数学模拟考试题卷
参考答案
一、选择题:(本大题共10个小题;每小题5分,共50分。)
|
题 号 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
答 案 |
D |
B |
C |
A |
D |
C |
A |
B |
A |
D |
二、填空题:(本大题共5小题,每小题5分,共25分。)
11、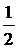 ; 12、
; 12、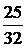 ;
;
13、1; 14 、720; 15、②④;
三、解答题:(本大题共6小题,共75分。)
16、(本小题满分12分)
解:(I) 当 x = 时,cos <a,c> = ………… 1分
= ………… 2分
= -cos x = -cos = cos ………… 3分
∵ 0≤<a,c>≤p, ………… 4分
∴ <a,c> = ………… 5分
(II) f (x) = 2a.b + 1 = 2 (-cos 2 x + sin x cos x) + 1 ………… 6分
= 2 sin x cos x-(2cos 2 x-1) ………… 7分
= sin 2x-cos 2x ………… 8分
= sin (2x-) ………… 9分
∵ x∈[,],∴ 2x-∈[,2p], ………… 10分
故 sin (2x-)∈[-1,] ………… 11分
∴ 当 2x-= ,即 x = 时,f (x)max = 1 ………… 12分
17、(本小题满分12分)
解:(I) n = 1 时,2.a1 = S1 = 3,∴a1 = ; …………2分
当 n≥2 时,2 n.an = Sn-Sn-1 = -6,∴ an = . 又 ≠ …………4分
∴ 通项公式an = …………6分
(II)当 n = 1 时,b1 = 2-log 2 = 3,∴ T1 = = ; …………8分
n≥2时, bn = n.(2-log 2) = n.(n + 1), ∴ = …………10分
∴ Tn = + + … + = + + + … + = -
∴ Tn = - …………12分
 |
 18、(本小题满分12分)
18、(本小题满分12分)
解:(Ⅰ)∵
B1D⊥平面ABC, AC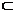 平面ABC,
平面ABC,
∴ B1D⊥AC, 又AC⊥BC,  BC∩B1D=D.
BC∩B1D=D.
∴ AC⊥平面BB1C1C. …………………… 3分
(Ⅱ) ∵ AC⊥平面BB1C1C ,要使AB1⊥BC1 ,由三垂线定理可知,
只须B1C⊥BC1, ………………………… 5 分
∴ 平行四边形BB1C1C为菱形, 此时,BC=BB1.
又∵ B1D⊥BC, 要使D为BC中点,只须B1C= B1B,即△BB1C为正三角形, ∴ ∠B1BC= 60°. ………………………… 7分
∵ B1D⊥平面ABC,且D落在BC上,
∴ ∠B1BC即为侧棱与底面所成的角.
故当α=60°时,AB1⊥BC1,且使D为BC中点…………………… 8分
(Ⅲ)过C1作C1E⊥BC于E,则C1E⊥平面ABC.
过E作EF⊥AB于F,C1F,由三垂线定理,得C1F⊥AB.
∴∠C1FE是所求二面角C1-AB-C的平面角.………………… 10分
设AC=BC=AA1=a,
在Rt△CC1E中,由∠C1BE=α=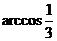 ,C1E=
,C1E=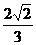 a.
a.
在Rt△BEF中,∠EBF=45°,EF=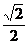 BE=
BE=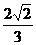 a.
a.
∴∠C1FE=45°,故所求的二面角C1-AB-C为45°.………… 12分
解法二:(1)同解法一 ……………… 3分
(Ⅱ)要使AB1⊥BC1,D是BC的中点,即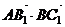 =0,||=||,
=0,||=||,
∴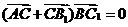 ,
, 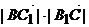 =0,∴
=0,∴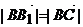 .
.
∴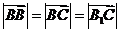 ,故△BB1C为正三角形,∠B1BC=60°;
,故△BB1C为正三角形,∠B1BC=60°;
∵ B1D⊥平面ABC,且D落在BC上, …………………… 7分
∴ ∠B1BC即为侧棱与底面所成的角.
故当α=60°时,AB1⊥BC1,且D为BC中点. …………………8分
(Ⅲ)以C为原点,CA为x轴,CB为y轴,经过C点且垂直于平面ABC的直线为z轴建立空间直角坐标系,则A(a,0,0),B(0,a,0),C(0,-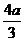 ,
,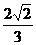 a),
a),
平面ABC的法向量n1=(0,0,1),设平面ABC1的法向量n2=(x,y,z).
由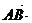 n2=0,及
n2=0,及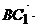 n2=0,得
n2=0,得
∴n2=(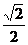 ,
,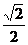 ,1).………………10分
,1).………………10分
cos<n1, n2>== ,
故n1 , n2所成的角为45°,即所求的二面角为45°.……………………12分
19、(本小题满分12分)
解:(I) x 的所有可能取值为3400,2400,1400,400.………………2分
(II) P(x = 3400) = ( ) 3 = ……………………4分
P(x = 2400) = C31( ) ( ) 2 = ………………6分
P(x = 1400) = C32( ) 2 ( ) = ………………8分
P(x = 400) = C33( ) 3 = ……………………10分
x 的分布列为
|
x |
3400 |
2400 |
1400 |
400 |
|
P |
|
|
|
|
……………………………………10分
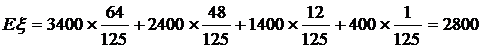 ……12分
……12分
20、(本小题满分13分)
解:(Ⅰ)设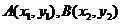 ,由
,由 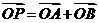 ,得
,得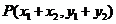
由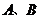 在双曲线上,有
在双曲线上,有
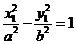 ①
①
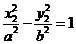 ②…………………………………………2分
②…………………………………………2分
由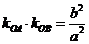 ,即
,即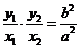 ,得
,得
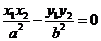 , ③………………………………………4分
, ③………………………………………4分
①+2×③+②,并整理,得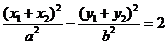
这表明点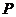 恒在双曲线
恒在双曲线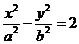 上.……………………………6分
上.……………………………6分
(Ⅱ)同(Ⅰ)所设,由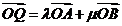 ,得
,得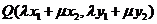
当点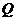 在双曲线的渐近线上,有
在双曲线的渐近线上,有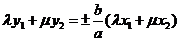
即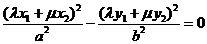 ,亦即
,亦即
 …………………10分
…………………10分
将①②③三式代入上式,得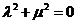 ,从而
,从而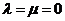 因此,不存在不同时为零的实数
因此,不存在不同时为零的实数 ,使得点
,使得点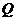 在题设双曲线的渐近线上.…………………13分
在题设双曲线的渐近线上.…………………13分
21、(本小题满分14分)
解:(I) 由题意得 f (e) = pe--2ln e = qe--2 ………… 1分
Þ (p-q) (e + ) = 0 ………… 2分
而 e + ≠0,∴ p = q ……………………………………………………3分
(II)由(I)知 f (x) = px--2ln x
f ' (x) = p + -= ……………………4分
令 h(x) = px 2-2x + p,要使 f (x) 在其定义域 (0,+¥) 内为单调函数,只需 h(x) 在 (0,+¥) 内满足:h(x)≥0 或 h(x)≤0 恒成立. ……………………5分
① 当 p = 0时, h(x) = -2x,∵ x > 0,∴ h(x) < 0,∴ f ' (x) = - < 0,
∴ f (x) 在 (0,+¥) 内为单调递减,故 p = 0适合题意. ………………………….6分
② 当 p > 0时,h(x) = px 2-2x + p,其图象为开口向上的抛物线,对称轴为 x = ∈(0,+¥),∴ h(x)min = p-
只需 p-≥0,即 p≥1 时 h(x)≥0,f ' (x)≥0,
∴ f (x) 在 (0,+¥) 内为单调递增,
故 p≥1适合题意. ……………………………………………7分
③当 p < 0时,h(x) = px 2-2x + p,其图象为开口向下的抛物线,对称轴为 x = Ï (0, + ¥).
只需 h(0)≤0,即 p≤0时 h(x)≤0在 (0, + ¥)恒成立.
故 p < 0适合题意. ……………………8分
综上可得, p≥1或 p≤0. ……………………………………………9分
另解:(II) 由 (I) 知 f (x) = px--2ln x
f’(x) = p + -= p (1 + )-
要使 f (x) 在其定义域 (0,+¥) 内为单调函数,只需 f’(x) 在 (0,+¥) 内满足:f’(x)≥0 或 f’(x)≤0 恒成立.
由 f’(x)≥0 Û p (1 + )-≥0 Û p≥ Û p≥()max,x > 0
∵ ≤ = 1,且 x = 1 时等号成立,故 ()max = 1
∴ p≥1
由 f’(x)≤0 Û p (1 + )-≤0 Û p≤ Û p≤()min,x > 0
而 > 0 且 x → 0 时,→ 0,故 p≤0
综上可得,p≥1或 p≤0
(III) ∵ g(x) = 在 [1,e] 上是减函数
∴ x = e 时,g(x)min = 2,x = 1 时,g(x)max = 2e
即 g(x) Î [2,2e] ………… 10分
① p≤0 时,由 (II) 知 f (x) 在 [1,e] 递减 Þ f (x)max = f (1) = 0 < 2,不合题意。 …… 11分
② 0 < p < 1 时,由x Î [1,e] Þ x-≥0
∴ f (x) = p (x-)-2ln x≤x--2ln x
右边为 f (x) 当 p = 1 时的表达式,故在 [1,e] 递增
∴ f (x)≤x--2ln x≤e--2ln e = e--2 < 2,不合题意。…… 12分
③ p≥1 时,由 (II) 知 f (x) 在 [1,e] 连续递增,f (1) = 0 < 2,又g(x) 在 [1,e] 上是减函数
∴ 本命题 Û f (x)max > g(x)min = 2,x Î [1,e]
Þ f (x)max = f (e) = p (e-)-2ln e > 2
Þ p > (∵ >1) ………… 13分
综上,p 的取值范围是 (,+¥) ………… 14分